Богатство языка программирования
Это программа для моделирования одного шага эволюции клеточной системы.
| LifeStep[a_List] := MapThread[If[(#1 == 1 && #2 == 4) || #2 == 3, 1, 0]&, {a, Sum[RotateLeft[a, {i, j}], {i, -1, 1}, {j, -1, 1}]}, 2] |
А это пример оптимизированной программы, которая оперирует сосписками живых клеток.
| LifeStep[list_] := With[{u=Split[Sort[Flatten[Outer[Plus,list,N9,1] ,1]]]}, Union[Cases[u,{x_,_,_}->x], Intersection[Cases [u,{x_,_,_,_}->x],list]]] N9=Flatten[Array[List,{3, 3},-1], 1] ; |
Система Mathematica позволяет легко создавать программы, состоящие из нескольких компонент.
Здесь приведены составляющие программы, моделирующей поведение клеточных систем
| CenterList[n_Integer]:=ReplacePart[Table[0, {n}], 1, Ceiling[n/2]] ElementaryRule [num_Integer] := IntegerDigits[num, 2, 8] CAStep[rule_List, a_List] :=rule[[ 8 - (RotateLeft[a] + 2 (a + 2 RotateRight[a])) ]] CAEvolveList[rule_List, init_List, t_Integer] :=NestList[CAStep[rule, #]&, init, t] CAGraphics[history_List] :=Graphics[Raster[1 - Reverse[history]], AspectRatio -> Automatic] |
Пример работы программы.
Show[CAGraphics[ CAEvolveList[ElementaryRule[30], CenterList[101], 50]] ];
 |
Mathematica имеет компилятор для оптимизации программ, которые работают со списками и числами.
| CAStep = Compile[{{rule, _Integer, 1}, {a, _Integer,1}}, rule[[ 8 - (RotateLeft[a] + 2 (a + 2 RotateRight[a])) ]]] |
Программы системы Mathematica зачастую являются прямой трансляцией теоретических положений справочной литературы.
Здесь вводятся необходимые определения для расчета импеданса электрической цепи.
     |
Использование данных выше определений.
  |
Пример электрической схемы, заданной при помощи символической спецификации.
 |
Даже состоящая всего из одной строки программа системы Mathematica может выполнять сложные операции.
Эта программа моделирует одномерное случайное блуждание.
| RandomWalk[n_]:=NestList[(#+(-1) ^Random[Integer])&,0,n] |
График, демонстрирующий первые 200 шагов случайного блуждания.
ListPlot[RandomWalk[200],PlotJoined->True];
 |
Ясность программ системы Mathematica позволяет легко модифицировать их для более общих случаев.
Эта программа моделирует случайное блуждание в пространстве размерности d.
| RandomWalk[n_,d_]:=NestList[(#+(-1) ^Table[Random[Integer],{d}])&,Table[0,{d}],n] |
График трехмерного случайного блуждания.
Show[Graphics3D[Line[RandomWalk[1000,3]]]];
 |
Документы типа notebook являются чисто текстовыми иполностью переносимы.
Выбор пункта Show Expression в меню Format позволяет увидеть текстовую форму выражений документа.
Это типичная ячейка в документе типа notebook
 |
А это - то, что Вы получите, когда копируете интеграл во внешнее текстовое приложение типа программы работы с электронной почтой.
| \!\(\[Integral]\(Log[1 + \[Xi]]\/\@\[Xi]\)\ [DifferentialD]\[Xi]\) |
Документы типа notebook системы
Вы можете экспортировать графику и формулы в другие программам в форматах EPS, GIF и т.д., а затем манипулировать с ними.
Документы notebook системы Mathematica могут целиком экспортироваться в форматы HTML, TEX и RTF.

Единая форма записи символических
Химическая формула.
| HNO3Chemical[{Hydrogen,1},{Nitrogen,1},{Oxygen,3}] |
Электрическая цепь.
 |
Гибкость системы Mathematica дает
Дюжина способов определить факториал.
| f=Factorialf[n_] := n!f[n_] := Gamma[n-1]f[n_] := n f[n-1] ; f[1] = 1f[n_] := Product[i, {i, n}] f[n_] := Module[{t = 1}, Do[t = t*i, {i, n}]; t] f[n_] := Module[{t = 1, i}, For[i =1, i <=n, i++, t *= i]; t]f[n_] := Apply[Times, Range[n]]f[n_] := Fold[Times, 1, Range[n]]f[n_] := If[n == 1, 1, n f[n-1]]f = If[#1 == 1, 1, #1 #0[#1 - 1]]&f[n_] := Fold[#2[#1]&, 1, Array[Function[t, #t]&, n]] |
Эта команда сбрасывает значения, приписанные f.
| Clear[f] |
| Предыдущая глава | Оглавление | Следующая глава |
Использование различных алгоритмов в системе Mathematica
Использование различных алгоритмов в системе Mathematica
Всякий раз, используя систему Mathematica, Вы обращаетесь к самой большой в мире коллекции вычислительных алгоритмов.
Mathematica автоматически выбирает соответствующие алгоритмы для каждого вычисления.
| FindRoot[Cos[x]==x+Log[x],{x,1}]{x->0.840619} |
| NIntegrate[Log[x+Sin[x]],{x,0,2}]0.555889 |
| NSolve[x^5-6x^3+8x+1==0,x]{{x->-2.05411},{x->-1.2915},{x->-0.126515}, {x->1.55053},{x->1.9216}} |
Mathematica использует современные алгоритмы для разложения на множители целых чисел. Результат приведен в виде списка сомножителей и соответствующих показателей степеней.
| FactorInteger[2^105-1]{{7,2},{31,1},{71,1},{127,1},{151,1},{337,1}, {29191,1},{106681,1},{122921,1},{152041,1}} |
Эта команда генерирует двумерную таблицу.
| m=Table[2^i + x^j,{i,3},{j,4}] {{2+x,2+x2,2+x3,2+x4},{4+x,4+x2,4+x3,4+x4}, {8+x,8+x2,8+x3,8+x4}} |
Представление таблицы в форме матрицы.
MatrixForm[m] |
Вычисление ядра матрицы.
| NullSpace[m]{{x+x2,-1-x-x2,0,1},{x,-1-x,1,0}} |
Mathematica может решать дифференциальные уравнения как численно, так и в аналитической форме.
Ниже Mathematica численно решает нелинейное дифференциальное уравнение. Ответ - интерполяционная функция, которая представляет решение в неявной форме.
| NDSolve[{x''[t]+x[t]^3==Sin[t],x[0]==x'[0]==0},x, {t,0,50}]{{x->InterpolatingFunction[{{0.,50.}},<>]}} |
Параметрический график решения. Команда /. означает, что Mathematica должна подставить предыдущее решение вместо x[t].
ParametricPlot[Evaluate[{x[t],x'[t]}/.%],{t,0,50}]
 |
| Предыдущая глава | Оглавление | Следующая глава |
Язык системы Mathematica может применяться, чтобы точно определить все параметры документа.
Пример типичной ячейки в документе системы Mathematica.
| Это пример ячейки в документе notebook. |
Это внутреннее представление ячейки.
| Cell["Это пример ячейки в документе notebook.", "Text", CellFrame->True, FontWeight->"Bold", FontSlant->"Italic", Background->RGBColor[0, 1, 1], CellTags->"T.8"] |
Каждый рабочий документ системы
Документы типа notebook автоматически организованны в виде иерархии ячеек. Вы можете сворачивать группы ячеек, оставляя на виду только их заголовки. Вы можете использовать гиперссылки как для переходов внутри документа, так и для связи с другими документами. Каждой ячейке может быть приписан свой стиль из встроенной коллекции стилей. Документы остаются неизменными при выводе как на экран, так и на принтер, так как система Mathematica в каждом случае автоматически подбирает шрифты и компоновку документа. Система Mathematica содержит сотни управляющих параметров, которые позволяют Вам придавать документам типа notebook любой вид и создавать документы типографского качества.
Это обычный текст. Он может быть набран любым шрифтом и иметь любую форму, размер, цвет и т.д. Вы можете также вставлять в текст специальные символы типа
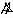
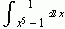
Система Mathematica упрощает создание таблиц и массивов.
 |
Mathematica позволяет легко выравнивать и позиционировать текст.
Подобно другим объектам в системе Mathematica ячейки в документе типа notebook и весь документ в целом в конечном счете - набор команд языка системы Mathematica. Используя стандартный интерфейс системы, Вы можете при помощи команды Show Expression увидеть внутреннее представление любой ячейки документа.
Легко изготовить Ваши собственные палитры.
Вы можете создавать новые палитры, используя подраздел Create Table/Matrix/Palette раздела меню Input.
 |
Mathematica использует шаблоны, чтобы обобщить понятие функции.
Это стандартный способ определения функции для всех значений x.
 |
Изменение общего определения функции при фиксированном значении аргумента.
| f[0]:=e |
Пример использования определенной выше функции f.
f[6]+f[a+b]+f[0]
 |
Сброс определения функции f.
| Clear[f] |
Mathematica может оперировать
| 1000! 40238726007709377354370243392300398571937486421071463\ 25437999104299385123986290205920442084869694048004799\ 88610197196058631666872994808558901323829669944590997\ 42450408707375991882362772718873251977950595099527612\ 08749754624970436014182780946464962910563938874378864\ 87337119181045825783647849977012476632889835955735432\ 51318532395846307555740911426241747434934755342864657\ 66116677973966688202912073791438537195882498081268678\ 38374559731746136085379534524221586593201928090878297\ 30843139284440328123155861103697680135730421616874760\ 96758713483120254785893207671691324484262361314125087\ 80208000261683151027341827977704784635868170164365024\ 15369139828126481021309276124489635992870511496497541\ 99093422215668325720808213331861168115536158365469840\ 46708975602900950537616475847728421889679646244945160\ 76535340819890138544248798495995331910172335555660213\ 94503997362807501378376153071277619268490343526252000\ 15888535147331611702103968175921510907788019393178114\ 19454525722386554146106289218796022383897147608850627\ 68629671466746975629112340824392081601537808898939645\ 18263243671616762179168909779911903754031274622289988\ 00519544441428201218736174599264295658174662830295557\ 02990243241531816172104658320367869061172601587835207\ 51516284225540265170483304226143974286933061690897968\ 48259012545832716822645806652676995865268227280707578\ 13918581788896522081643483448259932660433676601769996\ 12831860788386150279465955131156552036093988180612138\ 55860030143569452722420634463179746059468257310379008\ 40244324384656572450144028218852524709351906209290231\ 36493273497565513958720559654228749774011413346962715\ 42284586237738753823048386568897646192738381490014076\ 73104466402598994902222217659043399018860185665264850\ 61799702356193897017860040811889729918311021171229845\ 90164192106888438712185564612496079872290851929681937\ 23886426148396573822911231250241866493531439701374285\ 31926649875337218940694281434118520158014123344828015\ 05139969429015348307764456909907315243327828826986460\ 27898643211390835062170950025973898635542771967428222\ 48757586765752344220207573630569498825087968928162753\ 84886339690995982628095612145099487170124451646126037\ 90293091208890869420285106401821543994571568059418727\ 48998094254742173582401063677404595741785160829230135\ 35808184009699637252423056085590370062427124341690900\ 41536901059339838357779394109700277534720000000000000\ 00000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000\ 000000000000000000000000 |
Mathematica способна проводить вычисления с любой заданной точностью.
Здесь приведено значение числа pi, вычисленное с 500 знаками.
 |
Разложение полинома на множители.
Factor[x99 + y99]
 |
| Simplify[%]x99 + y99 |
Mathematica может оперироватьне только с числами, но и с данными любого типа.
Считывание всех элементов словаря.
| data=ReadList["dictionary.dat",String]; |
Выбор первых 40 слов в словаре.
| Take[data,40] {"a","AAA","AAAS","Aarhus","Aaron","ABA","Ababa", "aback","abacus","abalone","abandon","abase","abash", "abate","abbas","abbe","abbey","abbot","Abbott", "abbreviate","abc","abdicate","abdomen","abdominal", "abduct","Abe","abed","Abel","Abelian","Abelson", "Aberdeen","Abernathy","aberrant","aberrate", "abet","abetted","abetting","abeyance","abeyant", "abhorred"} |
Выбор слов, которые являются палиндромами и содержат более двух букв.
| Select[data,(#==StringReverse[#] && StringLength[#]>2)&] {"AAA","ABA","ala","AMA","ana","bib","bob","bub","CDC", "civic","dad","deed","did","DOD","dud","eke","ere", "eve","ewe","eye","gag","gig","gog","huh","iii", "level","madam","minim","mum","non","noon","nun","pap", "PDP","peep","pep","pip","poop","pop","pup","radar", "refer","rever","rotor","sis","s's","tat","teet", "tenet","tit","TNT","toot","tot","wow"} |
Эта команда находит длины всех слов в словаре.
| wordLengths=Map[StringLength,data]; |
Подсчет общего числа слов равной длины.
| Table[Count[wordLengths,i],{i,Max[wordLengths]}]{26,131,775,2152,3093,3793,3929,3484,2969,1883,1052, 542,260,102,39,15,6,4,0,1,2,1} |
ListPlot[%,PlotStyle->PointSize[0.02]]; |
| Предыдущая глава | Оглавление | Следующая глава |
Mathematica объединяет компактность математической системы обозначений с точностью машинного языка.
Ввод интеграла с использованием только обычных символов клавиатуры.
Integrate[Log[1+x]/Sqrt[x],x]
 |
Тот же самый интеграл, введенный в естественной форме. Ввод в такой форме осуществляется с помощью палитр или непосредственно с клавиатуры.
  |
Mathematica всегда позволяет Вам отредактировать полученный результат и использовать его снова как исходное выражение.
  |
Система Mathematica может выводить результат в традиционном для математической литературе виде. Следует учесть, что запись в стандартной форме (StandardForm) абсолютно точна и однозначна, в то время как традиционная форма требует некоторой эвристики для интерпретации.
Вычисление интеграла и вывод результата в традиционной форме (TraditionalForm).
  |
Mathematica способна создавать высококачественные формулы любой сложности и величины.
  |
Большое количество математических формул, созданных в системе Mathematica, содержится в Галерее формул из раздела Демонстрация возможностей системы Mathematica 3.0.
Система Mathematica легко работает с абстрактной системой обозначений.
  |
Система Mathematica поддерживает свыше 700 специальных символов посредством своих новых шрифтов, оптимизированных как для печати, так и для вывода на дисплей.
| Предыдущая глава | Оглавление | Следующая глава |
Mathematica осведомлена о сотнях специальных функций, используемых в чистой и прикладной математике.
LegendreQ[3, x]
 |
Система Mathematica может вычислять значения специальных функций с любыми параметрами и с любой точностью.
| N[MathieuC[1+I,2 I,3],40] 3.92513113741251986434976461681583792036+1. 898823911543347241105274797143911577679 I |
Mathematica позволяет легко создавать изумительныемультимедийные эффекты.
Трехмерный параметрический график с автоматическим выбором большинства опций.
  |
Тот же график с заданием ряда специфических опций.
  |
Mathematica позволяет создавать не только статичную, но и анимированную графику.
Чтобы увидеть анимацию, щелкните мышью по графику.
  |
Это еще один пример анимации.
  |
Mathematica работает на всех основных
Стандартная система Mathematica состоит из двух частей:
  |
Документы типа notebook системы Mathematica полностью совместимы со всеми компьютерными системами.

Работая с одним документом notebook, Вы можете запускать несколько копий ядра системы Mathematica, причем как на локальном, так и на удаленных компьютерах.
Mathematica также дает Вам возможность генерировать звук.
Эта команда производит звук с заданной формой волны.
  |
Mathematica включает в себя графические
Эта команда генерирует длинный список графических примитивов, изображающих точку.
 |
Здесь из списка выбирается пять элементов.
Take[%,5]
 |
График, соответствующий списку примитивов.
Show[Graphics[gr, Frame-> True]]
 |
Создание списка трехмерных примитивов, изображающих куб.
| gr=Flatten[Table[If[Mod[Multinomial[x,y,z],2]==1, Cuboid[1.2{x,y,-z}],{}],{x,0,15}, {y,0,15},{z,0,15}]]; |
Выбор первых пяти элементов в списке.
| Take[%,5]{Cuboid[{0,0,0}], Cuboid[{0,0,-1.2}], Cuboid[{0,0,-2.4}] ,Cuboid[{0,0,-3.6}], Cuboid[{0,0,-4.8}]} |
Эта команда рисует график, соответствующий списку примитивов.
Show[Graphics3D[gr]]
 |
MathLink может также использоваться
MathLink позволяет устанавливать шаблоны, чтобы точно определить, каким образом должны вызваться внешние программы. Это определяет связь с библиотекой подпрограмм языка C.
| :Begin: :Function: anneal :Pattern: TSPTour[r:{{_, _}..}] :Arguments: {First[Transpose[r]], Last[Transpose[r]], Length[r], Range[Length[r]]} :ArgumentTypes: {RealList, RealList, Integer, IntegerList} :ReturnType: Manual :End: |
Создание в системе Mathematica трехмерного графика.
  |
Это изображение было получено с использованием возможностей внешнего графического редактора, в который оно было передано из системы Mathematica через протокол MathLink.

Вы можете использовать MathLink, чтобы управлять интерфейсом системы Mathematica из ее ядра.
Эта команда сообщает интерфейсу системы, что надо открыть окно, содержащее палитру цветов.
| FrontEndTokenExecute["ColorSelectorDialog"] |
Можно использовать MathLink, чтобы
На большинстве компьютерных систем (обычно исключение составляет Macintosh) эта команда запускает дополнительное ядро системы Mathematica на Вашем компьютере.
| link=LinkLaunch["MathKernel -mathlink"]; |
Команда чтения данных из дополнительного ядра.
| LinkRead[link]InputNamePacket["In[1]:= "] |
Запись команды в дополнительное ядро.
| LinkWrite[link,Unevaluated[$SessionID]] |
Считывание $SessionID из вспомогательного ядра.
| LinkRead[link]ReturnPacket[20002811790628968292] |
Значение $SessionID в Вашем главном ядре будет отличаться.
| $SessionID20000841219624707995 |
Закрытие дополнительного ядра.
| LinkClose[link]; |
| Предыдущая глава | Оглавление | Следующая глава |
Объектно-ориентированное программирование
Задание трех свойств объекта h.
| h/:h[x_]+h[y_]:=hplus[x,y]h/:p[h[x_],x_]:=hp[x]h/:f_[h[x_]]:=fh[f,x] |
Пример использования данного выше определения для объекта h.
| h[a]+h[b]+f[h[r]]+h[h[x]]fh[f,r]+fh[h,x]+hplus[a,b]Clear[h] |
Палитры работают как дополнительная клавиатура.
В палитре, подобной этой, нажатие кнопки
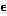
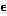
   |
В этой палитре значок

 |
Нажатие кнопки вносит выделенное выражение под знак радикала.
  |
Построение документа типа notebook
Эта команда, создающая три ячейки в стиле заголовка подраздела.
| Do[StylePrint[StringJoin["Заголовок", ToString[i]], "Subsubsection"],{i,3}] |
Процедурное программирование.
| z=a;Do[Print[z*=z+i],{i,3}]a (1+a)a (1+a) (2+a (1+a))a (1+a) (2+a (1+a)) (3+a (1+a) (2+a (1+a)))Clear[z] |
Программа в системе Mathematica
Это программа, отвечающая модели Kohmoto для спектра энергии квантовой частицы в одномерном квазипериодическом потенциале.
FareySequence[q_]:=Apply[Union,Array[Range[#-1]/#&,q]]
      |
Пример работы программы.
Show[Graphics[SpectrumData /@ FareySequence[20]]]
 |
| Предыдущая глава | Оглавление | Следующая глава |
Программирование, ориентированное на работу с функциями.
| NestList[f,x,4]{x,f[x],f[f[x]],f[f[f[x]]],f[f[f[f[x]]]]} |
Здесь символ # является областью, замещаемой аргументом функции.
NestList[(1 + #)2 &, x, 3] |
| p[x_+y_]:=p[x]+p[y]p[a+b+c]p[a]+p[b]+p[c] |
Символ _ замещает одно единственное выражение; символ __ замещает любую последовательность выражений.
| s[{x__,a_,y__},a_]:={a,x,x,y,y}s[{1,2,3,4,5,6},4]{4,1,2,3,1,2,3,5,6,5,6}Clear[p, s] |
Программирование, ориентированное на работу со списками.
Многие операции автоматически работают со списками.
| 1 + {a, b, c}2{1 + a2, 1 + b2, 1 + c2} |
| Table[ij, {i, 4}, {j, i}]{{1},{2,4},{3,9,27},{4,16,64,256}} |
Объединение вложенных списков.
| Flatten[%]{1,2,4,3,9,27,4,16,64,256} |
Разбиение предыдущего списка на подмножества длины 2.
| Partition[%,2]{{1,2},{4,3},{9,27},{4,16},{64,256}} |
Программы в системе Mathematica предоставляют беспрецедентно ясные способы записи алгоритма.
Обе эти программы аппроксимируют Золотое Сечение с точностью до k знаков.
   |
Протокол MathLink обеспечивает связь между системой Mathematica и внешними программами.
Это код языка C для посылки некоторого выражения из внешней программы в систему Mathematica.
| /* Integrate[Sqrt[Log[x]], x] */ MLPutFunction( stdlink, "EvaluatePacket", 1); MLPutFunction( stdlink, "Integrate", 2); MLPutFunction( stdlink, "Sqrt", 1); MLPutFunction( stdlink, "Log", 1); MLPutSymbol( stdlink, "x", 1); MLPutSymbol( stdlink, "x"); MLEndPacket( stdlink); |
Эта команда подключает компилируемую внешнюю программу C, которая выполняет поразрядные операции с целыми числами.
| link=Install["bitops"]; |
Выполнение внешней функции BitAnd.
| BitAnd[22222,33333]516 |
Отключение внешней программы.
| Uninstall[link]; |
Сегодня система Mathematica
Системе Mathematica посвящены сотни книг на более чем десяти языках.

Существуют специальные периодические издания, посвященные системе Mathematica.

Имеется растущая библиотека профессиональных прикладных программ, базирующихся на системе Mathematica.

Сотни учебных курсов были разработаны с использованием системы Mathematica.

Wolfram Research's MathSource - колоссальный архив материалов, относящихся к системе Mathematica.

При разработке и эксплуатации самых разнообразных изделий используется система Mathematica.

Web-представительство http://www.wolfram.com/ разработчика системы Mathematica компании Wolfram Research Inc. содержит тысячи страниц материала и постоянно обновляется.

| Предыдущая глава | Оглавление |
Система Mathematica дает Вам в
Эта команда генерирует матрицу размера 100x100, состоящую из случайных чисел. Точка с запятой в конце команды запрещает системе Mathematica вывод матрицы на экран.
| m=Table[Random[ ],{100},{100}]; |
На большинстве компьютеров система Mathematica затрачивает меньше секунды на вычисление всех собственных значений этой матрицы и представление их модулей в виде графика.
ListPlot[Abs[Eigenvalues[m]]]
 |
Система Mathematica имеет модульную
Пример ввода/вывода в стандартном интерфейсе системы Mathematica.
  |
Вы можете также обращаться к ядру системыMathematica непосредственно с текстового терминала.
| Integrate[Sqrt[Log[x]], x]
1 -(-) Sqrt[Pi] Erfi[Sqrt[Log[x]]] + x Sqrt[Log[x]] 2 |
Система Mathematica имеет свои, независимые от операционной системы, функции для управления файлами.
Вывод списка всех файлов типа notebook в Вашем корневом каталоге.
| files=FileNames["*.nb", $HomeDirectory] |
| Предыдущая глава | Оглавление | Следующая глава |
Система Mathematica позволяетимпортировать
Чтение данных из файла image.dat. Точка с запятой после команды запрещает системе Mathematica выводить данные на экран.
| data=ReadList["image.dat",Number,RecordLists->True]; |
Визуализация данных в виде графика плотности.
ListDensityPlot[data,Mesh->False, FrameTicks->None]; |
Вы можете применять к данным любую функцию системы Mathematica.
ListDensityPlot[Exp[Sqrt[data]],Mesh->False, FrameTicks->None,ColorFunction->Hue]; |
Здесь осуществлен последовательный сдвиг данных вправо.
ListDensityPlot[MapIndexed[RotateRight,data], Mesh->False,FrameTicks->None,ColorFunction->Hue]; |
Представление данных в виде контурного графика.
ListContourPlot[data,ContourShading->False, Contours->6,FrameTicks->None]; |
График плотности данных с сохранивших только несколько Фурье-компонент.
ListDensityPlot[Re[InverseFourier[ MapIndexed[If[Max[#2]<60,#,0]&,Fourier[data],{2}]]], Mesh->False,FrameTicks->None];
 |
Распределение градаций серого в данных.
ListPlot[Sort[Flatten[data]]]; |
Представление данных в виде трехмерного графика.
ListPlot3D[data,ColorFunction->Hue,Mesh->False, ViewPoint->{0.2,-2,5}];
 |
Система Mathematica сделала возможным
| Предыдущая глава | Оглавление | Следующая глава |
Система Mathematica способна взять
  |
  |
  |
Система Mathematica может вычислять также конечные и бесконечные суммы и произведения.
  |
Большое количество подобных примеров содержится в демонстрационном документе Интегралы, суммы и произведения из раздела Демонстрация возможностей системы Mathematica 3.0.
Mathematica может решать широкий класс обыкновенных дифференциальных уравнений и уравнений в частных производных.
DSolve[y''[x]+y'[x]+x y[x]==0, y[x], x]
 |
Встроенные алгоритмы системы Математика способны справиться с широким спектром математических задач.
  |
 |
TrigReduce[Cos[x]4]
 |
Нахождение миллиардного простого числа при совместном использовании встроенных таблиц и алгоритмов.
| Prime[109]22801763489 |
| Предыдущая глава | Оглавление | Следующая глава |
Система Mathematica включает в
Mathematica объединяет в себе самые разные методы программирования, что позволяет Вам всегда применять в данный момент наиболее подходящие из них.
Систему Mathematica можно использовать как калькулятор: Вы вводите задание и получаете результат.
Пример простейшего вычисления. Нажатие клавиш Shift-Enter является приказом системе Mathematica вычислить введенное выражение.
| 6^203656158440062976 |
Mathematica автоматически обрабатывает числа любого размера.
| 6^200 42682522381202740079697489151877373234298874535448942\ 94954790789351129295496197390190721393407570972968128\ 15466676129830954465240517595242384015591919845376 |
Вы можете работать в стандартной математической форме записи, используя палитры или специальные сочетания клавиш. Подробнее эти возможности будут описаны ниже.
| 6200 42682522381202740079697489151877373234298874535448942\ 94954790789351129295496197390190721393407570972968128\ 15466676129830954465240517595242384015591919845376 |
Вычисление собственных значений матрицы.
  |
Смешанные методы программирования.
Наиболее мощные операторы системы Mathematica объединяют в себе различные методы программирования.
| Position[{1,2,3,4,5}/2,_Integer]{{2},{4}} |
| MapIndexed[Power,{a,b,c,d}]{{a}, {b2}, {c3}, {d4}} |
 |
| ReplaceList[{a,b,c,d,e},{x__,y__}->{{x},{y}}]{{{a},{b,c,d,e}},{{a,b},{c,d,e}},{{a,b,c},{d,e}}, {{a,b,c,d},{e}}} |
В программах системы Mathematica
Эта программа соответствует недавно открытой приближенной формуле для нахождения количества простых чисел, меньших заданного числа.
   |
Сравнение приближенного результата с точным значением, полученным с помощью встроенной функции PrimePi.
 |
Важная особенность использования
Определение функции g, аргументом которой является список, состоящий из двух элементов.
| g[{x_,y_}]:=x+yg[{4,a b}]4+a bClear[g] |
Определение функции, имеющей смысл площади круга, аргументом которой является объект Circle.
  |
Осуществление преобразования логического правила.
| reduce[p_ && q_ || p_]:=p |
| Предыдущая глава | Оглавление | Следующая глава |
Важной особенностью системы Mathematica
Решение уравнения в системе Mathematica. Корни уравнения есть функции зависящие от параметра.
  |
Вычисление интеграла в системе Mathematica.
  |
Во многих видах вычислений система Mathematica является мировым рекордсменом по скорости.
В качестве примера здесь приведено одно вычисление из теории чисел; при больших значениях аргумента это вычисление было впервые выполнено в системе Mathematica всего за несколько минут.
| PartitionsP[8000] 783602643515683494905931450133645997190107693529858\ 6433111860020941782776452445099\0388402844164 |
| Предыдущая глава | Оглавление | Следующая глава |
Возможность манипулировать различными
Вычисление собственных чисел матрицы.
Eigenvalues[{{3, 1}, {2, 6}}]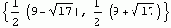 |
Система Mathematica способна вычислять собственные значения даже тогда, когда элементы матрицы являются символьными параметрами. В результате получается компактное представление собственных чисел для любого значения b.
v = Eigenvalues[{{3, 1}, {2, b}}] |
Все операции в системе Mathematica
Команда /. служит сигналом системе Mathematica применить подстановку b - > 1 + x.
| {a,b,c,d}/.b->1+x{a,1+x,c,d} |
Каждый символ x_ и y_ замещает любое выражение, так что шаблон x _ + y_ обозначает собой сумму любых двух объектов.
| {a + b, c + d, a + c} /. x_ + y_ -> x2 + y2{a2 + b2, c2 + d2, a2 + c2} |
| {a + b, c + d, a + c} /. a + x_ -> x3{b3, c + d, c3} |
Все символьные выражения записываются в единой форме head[arg1, arg2, ...].
Список элементов.
| {a,b,c}List[a,b,c] |
Алгебраическое выражение.
 |
Уравнение.
| x==Sin[x]Equal[x,Sin[x]] |
Логическое выражение.
| p&&!qAnd[p,Not[q]] |
Команда.
 |
Графика.
 |
Абстрактная математическая запись.
 |
Кнопка.
 |
Ячейка в документе системы Mathematica, содержащая текст.
| A cell containing textCell["A cell containing text","Text"] |
Встроенные функции системы Mathematica
Использование предыдущего результата для построения графиков функций, задающих собственные значения, в зависимости от параметра.
Plot[Evaluate[v], {b, -10, 10}]
 |
Вы можете найти значение b, при котором первое собственное значение равно нулю...
Solve[First[v] == 0, b] |
или найти интеграл от 0 до с от функции, задающей первое собственное значение.
  |
Теперь можно найти частичную сумму ряда Тейлора функции, являющейся результатом предыдущего интегрирования.
Series[%, {c, 0, 5}] |
Численное нахождение корня уравнения на заданном отрезке.
| FindRoot[int==1+c,{c,1}]{c->-0.554408} |
Простота работаты с формулами также важна при обработке данных.
Создание списка первых сорока простых чисел.
| Table[Prime[i], {i, 40}]{2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61, 67,71,73,79,83,89,97,101,103,107,109,113,127,131,137, 139,149,151,157,163,167,173} |
Приближение аппроксимирующей функцией.
| Fit[%, {Log[x],x,x2}, x]3.91287769352273429 x+0.0244902554054522703 x2-5.98809188219891908 Log[x] |
Вычисление суммы первых сорока простых чисел с применением аппроксимирующей функции.
| Sum[%, {x, 1, 40}]3090.16 |
Тот же результат, полученный точно.
| Sum[Prime[i],{i,1,40}]3087 |
Следующая команда объединяет в себе предыдущие и строит график разности между точными и приближенными значениями сумм простых чисел в зависимости от количества слагаемых.
  |
| Предыдущая глава | Оглавление | Следующая глава |
Вы можете использовать MathLink
Microsoft Word в качестве интерфейса системы Mathematica.

Web-страница, устанавливающая связь с системой Mathematica.

Microsoft Excel, связанный с системой Mathematica.

Вы можете использовать систему Mathematica для построения двумерных и трехмерных графиков функций.
Двумерный график простой функции.
Plot[Sin[x]+Sin[1.6x],{x,0,40}]
 |
Трехмерный график функции. Пробел между x и y эквивалентен символу умножения. Опция PlotPoints->30 задает количество ячеек сетки.
Plot3D[Sin[x y],{x,0,4},{y,0,4},PlotPoints->30]
 |
Вы можете воспользоваться большим количеством вычислительных возможностей системы Mathematica простым нажатием одной из кнопок в стандартных палитрах.
| Оглавление | Следующая глава |
Вы можете создавать заказные палитры, чтобы вводить любую функцию или оператор.
 |
При нажатии этой кнопки происходит факторизация выделенного выражения.
 |
| Предыдущая глава | Оглавление | Следующая глава |