Арифметические операторы

Математические выражения в системе Mathematica записываются с помощью операторов и функций. Операторы (от слова operator — исполнитель) являются элементами записи математических выражений, указывающими на то, какие действия производятся над символьными или числовыми данными. Когда эти данные используются совместно с операторами, их называют операндами.

Выражения, составленные из операторов, операндов и функций, способны возвращать результат своего вычисления. К примеру, если вычисляется сумма 2+3, то знак «+» является оператором, числа 2 и 3 — операндами, а вся запись 2+3 — выражением. Сами по себе операторы не возвращают какого-либо значения.

Существуют общепринятые приоритеты выполнения операций, например, в первую очередь выполняются сложение и вычитание, затем умножение и деление и далее другие операции. С помощью круглых скобок можно изменять последовательность выполнения действий, например, в выражении (2+3) М вначале будет вычислено 2+3, а затем уже результат будет умножен на число 4. В сомнительных случаях применение скобок особенно желательно, например 2^2+3 даст 7, а 2^ (2 + 3) даст 32.

Ниже перечислены основные операторы для выполнения арифметических операций (х, у и z — операнды, задающие данные, над которыми выполняются вычисления):

x+y+z  Сложение

x-y-z    Вычитание

х*у*z   или x у z    Умножение

х/у       Деление

х^у      Возведение х в степень у

Expr //N        Дает приближенное (с установленной точностью и                 формой) значение выражения ехрг

Полезно отметить, что знак пробела является арифметическим оператором умножения, если по обе стороны от него стоят операнды.

Как уже отмечалось, при выполнении вычислений особая роль принадлежит символам «%». Эти символы как сами по себе, так и в качестве аргументов функций используются для указания на применение результата предшествующих операций:

% — возвращает результат последней операции; %% — возвращает результат предпоследней операции; %...% — возвращает результат операции, выполненной в строке, отстоящей от конца на число повторений символа «%»; %n — возвращает результат операции в строке n. Нетрудно заметить, что применение этих символов облегчает выполнение последовательных вычислений.

Как уже отмечалось, для представления арифметических выражений ехрг в виде вещественного результата используется функция N[expr,m]. Можно также задать вычисление любого выражения в численном виде, используя выражение ехрг //N:

1/3+2/7

13/21

1/3+2/7 //N

0.619048

Таким образом, используя функцию N[expr,m] или вывод с помощью символов //N, можно организовать вычисления в режиме калькулятора, находясь в среде оболочки системы.

Если х имеет вещественное значение, то функция

MantissaExponent[x]

возвращает список, содержащий мантиссу и порядок приближенного вещественного числа х. Примеры:

123.456 10^10

1.23456 х1012

MantissaExponent[%]

{0.123456, 13}

Арифметические вычисления с повышенной точностью

Важное достоинство систем символьной математики — выполнение арифметических вычислений с произвольными разрядностью и точностью. Хотя на деле они ограничены объемом ОЗУ, но для современных компьютеров с объемом ОЗУ в единицы и десятки мегабайт вряд ли можно столкнуться со случаем, когда ограничения по разрядности и точности становятся существенными.

Следующие две функции, Rationalize [х] и Rationalize [x, dx], дают приближение для числа х в виде рациональных чисел. Вторая из этих функций задает приближение с заданной точностью dx.

Mathematica может работать с большими числами и выполнять определенные операции с очень высокой точностью. Примеры, приведенные на рис. 3.3, иллюстрируют эти возможности.

Как видно из примеров представления рациональных чисел, результат приближения зависит от заданной погрешности. Чем она меньше, тем большие значения целых чисел в числителе и знаменателе результата разыскивает система.


Функция Rationalize открывает широкие возможности для разработки целочисленных алгоритмов вычислений, позволяя легко получать рациональные приближения для наиболее распространенных числовых констант — на рис. 3.3 примеры этого даны для числа 8.

Обратите внимание на последние два примера — вычисление факториала достаточно большого числа. Первый результат целочисленный: он занял целых три строки, но зато он точен. С помощью функции N [ехрг] результат всегда можно представить в виде большого вещественного числа — но приближенного. При этом может использоваться научная форма представления чисел — с мантиссой и порядком.



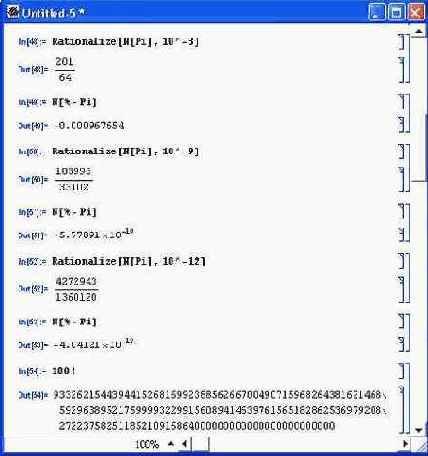
Рис. 3.3. Примеры представления чисел в разных формах

Укороченная форма записи арифметических операций

Спецификой систем Mathematica являются арифметические операторы с укороченной формой записи, объединяющие операцию присваивания с арифметической операцией. Эти довольно специфические операторы, хорошо известные пользователям языка С, представлены ниже вместе с соответствующими им функциями.

Функция	Оператор	Назначение
Increment [i]	i++	Увеличивает значение i на 1 после использования i в выражении
Decrement [i]	i --	Уменьшает значение i на 1 после использования i в выражении
Preincrement [i]	++i	Увеличивает значение i на 1 до использования i в выражении
PreDecrement [i]	--i	Уменьшает значение i на 1 до использования i в выражении
AddTo[x,d]	x += dx	Прибавляет dx к х и возвращает новое значение х
SubtractFrom[x,dx]	x -= dx	Отнимает dx от х и возвращает новое значение х _
TimesBy [х, с]	X **= 'С	Умножает х на с и возвращает новое значение х
DivideBy [х, с]	X /= С	Делит х на с и возвращает новое значение х

Применение укороченных операторов делает запись математических выражений более короткой, хотя наглядность их при этом несколько снижается. Ниже представлены примеры выполнения укороченных арифметических операций.

Ввод (In)	Вывод (Out)
i=0	0
++i; ++i; ++i	3
i=0; i++; i++; i++	2
i=5	5
-- i	4
i=5	5
i --	5
i --	4
x=5	5
x+=0 . 5	5.5
x-=0 . 5	5.
x*=2	10.
x/=5	2.

Численные данные

Двоичные числа, биты и байты

Минимальной единицей информации в компьютерной технике является двоичная единица — бит. Она имеет представление в виде 0 или 1, удобное для реализации простейшими электронными схемами с двумя состояниями электрического равновесия (например, триггерами или иными ячейками памяти). Многоразрядные двоичные числа представляют собой набор цифр 0 и 1, например, 100110 или 111001. Каждый старший разряд относительно предыдущего имеет весовой коэффициент, равный 2.

Именно с битами работает микропроцессор на нижнем уровне операций. Однако бит — слишком мелкая единица, не очень удобная в обращении. К тому же мы привыкли к куда более удобным и наглядным для нас элементам информации, таким как буквы, цифры, знаки арифметических операций, спецзнаки и символы псевдографики. В принципе, набор этих знаков, минимально необходимый для представления обычной текстовой и цифровой информации, содержит до 2 8 = 256 элементов. Каждый из них в компьютере представляется кодом от 0 до 255. Для задания таких кодов достаточно 8 бит (2^8=256), которые и образуют наиболее распространенную единицу представления информации — байт. 1024 байта образуют килобайт (Кбайт), 1024 Кбайт дают 1 Мбайт (мегабайт) и т. д.

Широко применяется общеизвестный стандарт кодирования текстовой информации ASCII (American Standard Code for Information Interchange).

Десятичные числа

К наиболее известным типам данных в математике относятся привычные нам десятичные числа (DECIMAL). Каждый разряд таких чисел имеет представление, заданное одной из арабских цифр — 0, 1, 2,..., 9. Весовой коэффициент старшего разряда относительно предшествующего равен 10. Количество цифр, представляющих число, может быть, в принципе, любым. Десятичные числа относятся к следующим основным типам.

Обозначение	Тип чисел	Примеры задания
Integer	Целочисленные	123	-345
Rational	Рациональные	123/567	-23/67
Real	Вещественные	123.	-123.45610 ^ 6
Complex	Комплексные	-3.5 + 0.	56 I

Десятичные числа наиболее распространены в научно-технических расчетах.

Целые числа

Целочисленные данные (Integer) — это целые числа, например 1, 2 или 123, которые представляются системой без погрешности и ограничения разрядности. Более того, арифметические операции над целыми числами система выполняет также без погрешностей и без ограничения числа цифр (рис. 3.1).



Рис. 3.1. Операции с целыми числами

Количество цифр, представляющих большое целое число, ограничено лишь его значением, но не какими-либо фиксированными форматами. Рациональные данные задаются отношением целых чисел, например 123/567, и также представляют результат точно. Поэтому система при символьных и численных расчетах всегда старается выдать результат в виде целых или рациональных чисел, там где это возможно:

1000000/3000000

1/3

(124-1)/(455+1)

41/152

Фактически целые числа произвольной разрядности в системах символьной математики представляются списками отдельных цифр. Особая организация списков повышает компактность представления больших целых чисел. Характерным примером работы с целыми числами большой разрядности является вычисление факториала n!=1*2*3*. . . *n. Примеры его вычисления уже приводились (см. рис. 1.16).

Числа с произвольным основанием

Для вычисления чисел с произвольным основанием используется конструкция

Основание^^Число

Число должно быть записано по правилам записи чисел с соответствующим основанием. Если основание больше 10, для обозначения значений чисел используются буквы от а до z. Наиболее известными из чисел с основанием системы счисления, превышающим 10, являются шестнадцатеричные числа (HEX — от слова hexagonal). Разряды таких чисел могут иметь следующие значения:

HEX 0123456789abCdef

DECIMAL 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

Каждый более старший разряд имеет весовой коэффициент относительно предыдущего разряда, равный 16.

Примеры задания шестнадцатеричного и двоичного чисел:

16^^123abcde

305839326

2^^1010111

87

Для представления чисел с произвольным основанием n (до 32) используется функция BaseForm[expr, n], которая возвращает выражение ехрг в форме числа с основанием n, которое указывается как подстрочный индекс.



Примеры использования функции BaseForm:

BaseForm[87,2]

10101112

BaseForm[305839326,16]

123abcde16

В дальнейшем мы будем использовать только десятичные числа.

Вещественные числа

Численные данные могут быть представлены также десятичными вещественными числами, которые могут иметь различную форму, например 123.456, 1.23456 10^2,12345.6 10^-2 и т. д. В общем случае они содержат мантиссу с целой и дробной частями и порядок, вводимый как степень числа 10. Как правило, вещественные числа в системах символьной математики могут иметь мантиссу с любым, но конечным числом знаков. Пробел между мантиссой и порядком эквивалентен знаку умножения *:

23.456*10^100

2.345бх10^101

10^-100

1/

100000000000000000000000000000

0000000000000000000000000000

0000000000000000000000000000000000000000000

10.^-100

1.x 10^-100

Как принято в большинстве языков программирования, целая часть мантиссы отделяется от дробной части точкой, а не запятой.

Mathematica производит операции с числами изначально как с целыми. Однако установка значка разделительной точки означает, что число должно рассматриваться как вещественное. Например, 1 — целое число, но 1. — уже вещественное число. Для представления выражения ехрг в форме вещественного числа используется функция N [ехрг] или N [ехрг, число_цифр_результата].

Примеры:

1/3

1/3

1./3 .

0.333333

N[1/3]

0.333333

N[2*Pi,50]

6.283185307179586476925286766559005768394338

Вещественные числа всегда имеют некоторую погрешность представления результатов из-за неизбежного округления и существования так называемого машинного нуля — наименьшего числа, которое воспринимается как нуль. В терминах системы Mathematica говорят о приближении числовых данных как об их аппроксимации, хотя в отечественной литературе под аппроксимацией чаще подразумевают описание некоторой зависимости между данными достаточно приближенной аналитической зависимостью.

Mathematica имеет две системные переменные, позволяющие вывести максимально и минимально возможные значения чисел, с которыми оперирует система:



$MaxMachineNumber

1.79769х10^308

$MinMachineNumber

2.22507х 10^-308

Обратите внимание на то, что функция N [ехрr, m] позволяет получить число с практическим любым числом цифр результата m. Разработчики последней версии Mathematica 4 утверждают, что это верно при количестве цифр результата до одного миллиона, что с лихвой удовлетворяет требованиям подавляющего большинства расчетов и вычислений.

Функции IntegerPart [x] и FractionalPart [x] обеспечивают возврат целой и дробной частей вещественного числа х:

N[Pi]

3.14159

IntegerPart[Pi]

3

FractionalPart[Pi]

-3.+ Л

N[FractionalPart[Pi]]

0.141593

Еще одна функция RealDigits [x] возвращает список реальных цифр результата и число цифр целой части х:

RealDigits[N[2*Pi]]

{{6, 2, 8, 3, 1, 8, 5, 3, 0, 7, 1, 7, 9, 5, 8, 6}, 1}

Есть и множество других функций для работы с вещественными числами. Они будут рассмотрены в дальнейшем. В Mathematica 4 функция RealDigits имеет расширенные формы, например RealDigits [x, b, len, n]. Для получения цифр мантиссы введены функции MantissaExponent [x] и MantissaExpo-nent[x,b].

Комплексные числа

Многие математические операции базируются на понятии комплексных чисел. Они задаются в форме

z=Re(z)+I*Im(z)

или

z=Re(z)+i Im (z)

где знак I (i) — мнимая единица (квадратный корень из -1), Re (z) — действительная часть комплексного числа, a Im (z) — мнимая часть комплексного числа. Пример задания комплексного числа:

2 + I3

или

2 + 3*I

Мнимая часть задается умножением ее значения на символ мнимой единицы I. При этом знак умножения * можно указывать явно или заменить его пробелом — в последнем случае комплексное число выглядит более естественным. Функции Re [ z ] и Im [ z ] выделяют, соответственно, действительную и мнимую части комплексного числа z. Это иллюстрируют следующие примеры:

Re[3+2*1]

3

Im[3+2 I]

2

Большинство операторов и функций системы Mathematica работают с комплексными числами. Разумеется, это расширяет сферу применения системы и позволяет решать с ее помощью различные специальные задачи — например, относящиеся к теории функций комплексного аргумента.Комплексные числа широко используются в практике электро- и радиотехнических расчетов на переменном токе.

Что нового мы узнали

В этом уроке мы научились:

Использовать основные классы данных системы Mathematica. Выполнять арифметические вычисления. Применять встроенные и пользовательские функции. Получать данные об объектах. Осуществлять подстановки. Работать со списками. Создавать массивы, векторы и матрицы. Пользоваться функциями линейной алгебры

Функции комплексного аргумента

Элементарные функции в системе Mathematica могут иметь аргумент в виде действительного числа х или комплексного z. Аргументы указываются как параметры функций в квадратных скобках.

Прежде всего отметим функции для работы с комплексными числами z:

Abs[z] — возвращает модуль комплексного числа z; Arg [ z ] — возвращает аргумент комплексного числа z; Conjugate [z] — возвращает комплексно-сопряженное с z число; Directedlnf inity [] — представляет бесконечную числовую величину с неопределенным направлением на комплексной плоскости; Directedlnfinity[z] — представляет бесконечную числовую величину, направление которой на комплексной плоскости определяется фазой комплексного аргумента z; Im [ z ] — возвращает мнимую часть комплексного числа z; Re [ z ] — возвращает вещественную часть числа z.

Далее приведены примеры операций с комплексными числами в непосредственном режиме.

Ввод (In)	Вывод (Out)
z1 : =2+1*3;
z2: =4+1*5;
N[zl+z2]	6. + 8.1 I
Re [2+1*3]	2
H[Im[z2]J	5.
N[zl/z2]	0.560976 + 0.0487805 I
N[Abs[zl*z2]]	23.0868
Con j ugate [ z 1 ]	2-31

Если ввести N [ z 1 / 0 ], то система выдаст следующее сообщение:

N[zl/0]

Power::infy : Infinite expression 1/0 encountered.

Complexlnfinity

Итак, в этом случае система выдает сообщение об ошибке, но после него возвращает константу Complexlnfinity, означающую комплексную бесконечность.

Функции линейной алгебры

Следующая группа функций системы Mathematica позволяет осуществлять над векторами и матрицами основные операции, используемые в линейной алгебре:

Cross [vl,v2, v3,...] — векторное произведение (может задаваться в виде v1*v2*v3*...); Det [m] — возвращает детерминант (определитель) квадратной матрицы m; DiagonalMatrix [list] — возвращает диагональную матрицу с главной диагональю, сформированной из элементов списка list, и нулевыми остальными элементами матрицы; Dot [a, b, с] — возвращает произведения векторов, матриц и тензоров. Операцию произведения можно задавать также в виде а. b. с; Eigensystem[m] — возвращает список {values, vectors} собственных значений и собственных векторов квадратной матрицы т; Eigenvalues [m] — возвращает список собственных значений квадратной матрицы m; Eigenvectors [m] — возвращает список собственных векторов квадратной матрицы m; IdentityMatrix [n] — возвращает единичную матрицу размером пхп (у нее диагональные элементы имеют значения 1, остальные 0); Inverse [m] — возвращает обратную матрицу для квадратной матрицы т, то есть матрицу m- 1 , которая, будучи умноженной на исходную матрицу, дает единичную матрицу; LinearSolve [m, b] — возвращает вектор х, представляющий собой решение матричного уравнения m. x==b, где m — матрица коэффициентов левой части системы линейных уравнений, х — вектор неизвестных и b — вектор свободных членов в правой части системы; Tr [list] — возвращает след матрицы или тензора (эта функция есть только у Mathematica 4); Transpose [m] — возвращает транспонированную матрицу, у которой столбцы и строки меняются местами в сравнении -с исходной матрицей m; RowReduce [m] — производит гауссовское исключение переменных, возвращая упрощенную форму матрицы m, полученную путем линейного комбинирования строк.

Следующие примеры иллюстрируют применение основных из этих функций.

Ввод (In)	Вывод (Out)
A: =IdentityMatrix [3]
А	{{1,	0,	0},	{0, 1, 0}, {0, 0, 1}}
MatrixExp [A]	{{E,	0,	0},	{0, E, 0}, {0, 0, E}}
MatrixQ [A]	True
MatrixPower [MatrixExp [A] , -1 . 5]	{{0. {0,	22313, 0, 0}, {0, 0.22313, 0), 0, 0.22313}}
А+{{1,2,3},{4,5,6},{7,8,9}}	{{2,	2,	3},	{4, 6, 6}, {7, 8, 10}}
m:={{1,2},{3,7}}
Inverse [m]	{{7,	-2}	, (	-3, 1}}
MatrixQ [m]	True
RowReduce [m]	{{1,	0},	{0	, 1}}

Вычисление детерминанта матрицы и функций, относящихся к собственным значениям, представлено на рис. 3.11.

Рис. 3.11. Вычисление детерминанта, собственных значений и векторов матрицы

Приведем еще несколько примеров:

m={{1,2},{3,7}}

{{1, 2}, {3, 7}}

Transpose[m]

{{1, 3), {2, 7}}

m//MatrixForm

1 2

3 7

Transpose[m]//MatrixForm

Inverse[m]//MatrixForm

7 -2

-3 1

В приложении указан ряд дополнительных матричных функций, применяемых реже, чем описанные выше функции.

Функции, опции, атрибуты и директивы

К важному типу объектов принадлежат функции — объекты, имеющие имя и список параметров, возвращающие некоторое значение в ответ на обращение к ним по имени с указанием списка конкретных (фактических) значений параметров. В системах Mathematica 2/3/4 встроенные функции задаются в виде

И дентификатор_Функции [ol, о2, o3, ...]

где ol, о2, оЗ... — объекты (параметры, опции, математические выражения и т. д.). Список входных параметров задается необычно — в квадратных скобках. В числе входных параметров могут быть специальные объекты — опции. Они задаются в виде

Имя_опции->3начение_опции

Значением опции обычно является то или иное слово. Например, в функции построения графиков

Plot [sin[x] , {x, 0,20} ,Axes->None]

опция Axes->None указывает на то, что отменяется вывод координатных осей (Axes). Функция Options [name] выводит для функции с идентификатором name список всех возможных для нее опций. Некоторые функции, например Sin, могут вообще не иметь опций, другие, такие как Solve, могут иметь целый «букет» опций:

Options [Sin]

Options [Solve]

{InverseFunctions -> Automatic, MakeRules -> False,

Method -> 3, Mode -> Generic, Sort -> True,

VerifySolutions -> Automatic, WorkingPrecision -> 00}

В последнем случае характер возвращаемого функцией результата может сильно зависеть от значений опций. Назначение каждой опции мы рассмотрим в дальнейшем. В этой главе они нам пока не понадобятся.

Каждый объект может характеризоваться некоторой совокупностью своих свойств и признаков, называемых атрибутами. Функция Attributes [name] возвращает список всех атрибутов функции с именем name, например:

Attributes [Sin]

{bistable, NumericFunction, Protected}

Attributes [Solve]

{Protected}

Как видите, для функции синуса характерны три атрибута:

bistable — указывает на применимость в списках и таблицах; NumericFunction — указывает на отношение к числовым функциям; Protected — указывает на то, что слово Sin защищено от какой-либо модификации.

Кроме того, в Mathematica 2/3/4 имеется понятие функций-директив. Эти функции не возвращают значений, а указывают, как в дальнейшем будут выполняться функции, работа которых зависит от директив. Синтаксис функций-директив тот же, что и у обычных функций.

Применение опций и директив делает аппарат функций более гибким и мощным, поскольку позволяет задавать те или иные свойства функций и условия их выполнения. Это особенно важно при использовании функций в задачах графики и символьной математики.

Функции пользователя

Хотя в систему входят многие сотни встроенных функций (начиная от элементарных и кончая специальными математическими функциями и системными функциями), нередко требуется расширить ее вводом новых функций, действие которых задается пользователем. Такие функции принято называть функциями пользователя. Функции пользователя — простейшие программные объекты, необходимые даже в том случае, когда пользователь не желает углубляться в тонкости программирования системы. Их цель — расширение системы и ее обучение работе с новыми функциями.

Для задания, опознавания и уничтожения функций пользователя используются следующие конструкции:

f (x_) := х^3 — отложенное задание функции пользователя с именем f; f (х_) = х^3 — немедленное задание функции пользователя с именем f; ?f — вывод информации о функции f; Clear [f] — уничтожение определения функции f.

В обозначениях вида х_ знак _ применяется для создания так называемых образцов, задающих локальные переменные в теле функции — в нашем примере это х. При этом в самом теле функции переменные обозначаются как обычно, без знака образца. Он лишь указывает на особый статус переменных в ограниченном пространстве программы — в теле функции. Так, если вместо х_ будет подставлено число 2, то f (2) будет возвращать 2 А 3. Вне тела функции значение переменной х не изменяется. Переменная х может быть и неопределенной: х_ определяет переменную х только для тела функции. Более подробно создание образцов будет описано в дальнейшем.

Mathematica позволяет записать введенные пользователем функции с их определениями на магнитный диск с помощью оператора

Save["filename", fl, f2, ...]

После этого функция пользователя становится внешней функцией. При этом для ввода таких функций в текущий документ (notebook) достаточно вызвать файл с именем filename:

<<filename

Рекомендуется создавать файлы с типовым расширением .т. Такие файлы входят в пакеты расширений системы. Имя файла нужно задавать по общепринятым для MS-DOS правилам, то есть при необходимости указывать логическое имя дисковода и путь к файлу, например, так:

<<D: \MAT\myfunc .m

Создание внешних функций по существу означает возможность расширения системы и ее адаптации к решению типовых задач конкретного пользователя. Как уже отмечалось, в систему входит мощная библиотека внешних расширений, и каждый пользователь может пополнить ее своими собственными библиотеками расширений.

Функции пользователя могут быть рекурсивными, то есть допускать в своем теле обращение к самим себе. Это связано с тем, что функция становится объявленной сразу же после задания своего имени со списком параметров. Рекурсия — мощный прием программирования, но злоупотреблять им не стоит. Многие рекурсивные алгоритмы более эффективно реализуются без рекурсии, с применением средств процедурного программирования, например циклов.

Функции пользователя можно задавать и выводить на печать как на языке системы, так и на некоторых общепринятых языках программирования, например Fortran, С или ТеХ. Для этого существует ряд функций преобразования, в имена которых входит слово Form (форма) и название языка для записи функций. Основные из них — это CForm [expr], FortranForm [expr ] и TeXForm [expr]. С их помощью выражения можно преобразовать в форму, принятую для языков программирования С, Fortran и ТеХ. При преобразовании в форму языка ТеХ греческие буквы заменяются их латинскими именами, например alpha, Alpha, beta, Beta, gamma и т. д. К сожалению, в отличие от систем класса MathCAD и Maple V R3, вывод математических формул в их полностью естественном виде не предусмотрен, хотя многое для этого уже сделано.

Для преобразования формул и данных, записанных на языке системы Mathematica и хранящихся в текстовых файлах, в другие формы используются следующие функции:

Splice ["file.rar"] — читает текстовый файл file.mx, интерпретирует его фрагменты, заключенные в ограничители <*...*>, и пишет текстовый файл file.*, в котором эти фрагменты преобразованы в формат, определяемый расширением х (с — С, f — Fortran, tex — ТеХ); Splice ["infile", "outfile"] — то же, но с раздельным заданием имен входного и выходного файлов. Таким образом, система Mathematica может общаться с другими программами, написанными на языках программирования, получивших распространение в практике реализации математических расчетов.Этому во многом способствует возможность преобразования форматов данных и результатов вычислений в различную форму, характерную для используемой внешней системы. К примеру, если вы работаете с программами на языке Fortran, то следует использовать соответствующий формат представления данных и результатов вычислений.

Mathematica может общаться также с иными системами, например текстовыми редакторами. К примеру, для передачи содержимого каких-либо ячеек в текстовый редактор Write, входящий в оболочку Windows, достаточно выделить эти ячейки и поместить их в буфер обмена, используя команду Сору из меню Edit. После этого надо запустить текстовый редактор и с помощью команды Edit | Paste поместить в окно редактирования содержимое ячеек. Если оно символьное, то с помощью редактора можно записать полученный документ с расширением .txt, то есть в стандартном текстовом формате, с которым работает большинство DOS-приложений.

Функции выявления структуры списков

Списки относятся к данным сложной структуры. Поэтому при работе с ними возникает необходимость контроля за структурой, иначе применение списков может привести к грубым ошибкам, как явным, сопровождаемым выдачей сообщения об ошибке, так и неявным. Последние могут привести к серьезным просчетам.

Для выявления структуры списков используется ряд функций:

Count [list, pattern] — возвращает количество элементов в списке list, которые соответствуют образцу pattern; Dimensions [list] — возвращает список размеров списка по каждой размерности; FreeQ [list, form] — возвращает True, если список list не содержит form; Length [list] — возвращает число элементов одномерного списка list или число размерностей в случае многомерного списка; MatrixQ [list ] — проверяет, является ли список матрицей, и дает True, если это так, и False в противном случае; MemberQ [list, form] — проверяет, есть ли form в списке, и возвращает True, если это так, и False в противном случае; Position [list, form] — возвращает номер позиции form в списке; TensorRank[list] — находит ранг списка, если он является тензором; VectorQ [list] — проверяет, является ли список вектором, и дает True, если это так, и False в противном случае.

Функции с буквой Q в конце имени являются тестирующими и возвращают логические значения True или False. Остальные функции возвращают численные значения соответствующего параметра списка.

Ниже даны примеры использования этих функций.

Ввод (In)	Вывод(Out)
11={1,2,3,4,1};
Length [11]	5
Dimensions [11]	{5}
MatrixQ [11]	False
TensorRank [ 11 ]	1
MemberQ[ll,l]	True
Count[ll,l]	2
FreeQ [11, 5]	True
Position [11,1]	{{1},{5}}
VectorQ [11]	True
M={{1, 2,3}, {4, 5, 6}}
Length [M]	2
Dimensions [M]	{2,3}

Система предоставляет пользователю свободу действий, производимых по результатам анализа структуры списков.

Генерация списков

Для генерации списков с элементами, являющимися вещественными и целыми числами или даже целыми выражениями, часто используется функция Table, создающая таблицу-список:

Table [expr, {imax} ] — генерирует список, содержащий imax экземпляров выражения ехрг; Table [expr, {i, imax} ] — генерирует список значений ехрг при 1, изменяющемся от 1 до imax; Table [expr, {i, imin, imax}] — генерирует список значений ехрг при i, изменяющемся от imin до imax; Table [expr, {i, imin, imax, di} ] — использует шаг приращения i, равный di; Table[expr, {i, imin, imax}, {j, jmin, jmax},...] —возвращает вложенный список. Самым внешним является список по переменной i.

Ниже приводятся примеры использования функции Table (первая строка каждого примера — ввод, следующая — вывод).

Пример	Комментарий
Table[i*j,{i,l,3},{j,l,3}] {{1, 2, 3), [2, 4, 6}, {3, 6, 9}}	Генерация матрицы размером
Table[N[Exp[i]], {1,0, 2,0.5}] {1., 1.64872, 2.71828, 4.48169, 7.38906}	Генерация пяти значений Е ^ 1 численном виде
Table[Exp[i],{i,l,5}] {е, е 2 , е 3 , е 4 , е 5 }	Генерация пяти значений Е ^ i (i=l, 2, 3,4 и 5)
Table[Exp[i],{5}]                        {е i , е i , е i , е i , е i }	Генерация пяти значений Е ^i

Применяется также функция Range, которая предназначена для создания так называемых числовых списков, значения которых равномерно распределены в некотором заданном диапазоне:

Range [imax] — генерирует список числовых элементов {1, 2, ..., imax}; Range [imin, imax] — генерирует список числовых элементов {imin, ..., Range [imin, imax, di] — генерирует список числовых элементов от imin до imax с шагом di.

Примеры использования функции Range.

Пример	Комментарий
Range [5] {1, 2, 3, 4, 5}	Генерация пяти целых чисел
Range[0,2,0.5] {0, 0.5, 1.,1.5, 2.}	Генерация чисел пяти вещественных

Изменение порядка расположения элементов в списке

Помимо добавления в список новых данных имеется возможность изменения порядка расположения элементов в списке. Она реализуется следующими операциями:

Flatten [list] — выравнивает (превращает в одномерный) список по всем его уровням; Flatten [list, n] — выравнивает список по п его уровням; Flatten [list, n, h] — выравнивает выражения с заголовком h no n уровням; FlattenAt [list, n] — выравнивает подсписок, если он оказывается п-м элементом списка list. Если n отрицательно, позиция отсчитывается с конца; Sort [list] — сортирует элементы списка list в каноническом порядке; Sort[list,p] — сортирует согласно функции упорядочения р; Reverse [list] — возвращает список с обратным порядком расположения элементов; RotateLeft [list] — возвращает список после однократного поворота влево; RotateLeft [list, n] — возвращает список после n-кратного поворота влево; RotateRight [list] — возвращает список после однократного поворота вправо; RotateRight [list, n] — возвращает список после n-кратного поворота вправо; Transpose [list] — осуществляет транспозицию (смену строк и столбцов) для двумерного списка; Transpose [list, п] — осуществляет транспозицию n-мерного списка. Ниже приведен ряд примеров на использование этих функций.

Ввод (In)	Вывод (Out)
13={{1,2,3},{4,5,6},{7,8,9}};	{1,2,3,4,5,6,7,8,9}
Flatten [13]
FlattenAt[13,l]	{1,2,3,{4,5,6},{7,8,9}}
Sort[{l,5,3,4,2}]	{1,2,3,4,5}
Reverse[{l,2,3,4}]	{4,3,2,1}
RotateLeft[ {1,2,3,4,5}, 2]	{3,4,5,1,2}
RotateRight[{l,2,3,4,5} ,2]	{4,5,1,2,3}
12={{a,b},{c,d}};
TableForm[12]	a b c d
TableFormf Transpose [12] ]	a c d b

Изменение порядка расположения элементов в списке полезно при реализации некоторых алгоритмов. К примеру, сортировка списка ускоряет выполнение статистических расчетов и уменьшает их погрешности.

Элементарные функции

Элементарные функции, надо полагать, хорошо известны читателю, взявшемуся за изучение Mathematica. Полный набор этих функций с их синтаксисом дан в приложении. Отметим, что в Mathematica имена элементарных функций записываются с большой буквы, а их аргументы задаются в квадратных скобках. Следующие примеры иллюстрируют сказанное.

Ввод (In)	Вывод (Out)
Sqrt[2]	Sqrt[2]
Sqrt[2.]	1.41421
2*Sin[l]	2 Sin[l]
N[2*Sin[l]]	1.68294
Log[Exp[l]]	1
Simplif у [Sin [x] /Cos [x] ]	Tan[x]
ComplexExpand [ Sin [ a+b* I ] ]	Cos[b] Sin[a]+ I Cosfa] Sinh[b)

Из этих примеров видно, что система знает и использует основные соотношения между элементарными функциями. В двух последних примерах используются символьные преобразования с применением функций Simplify (упрощение выражений) и ComplexExpand (расширение выражений с комплексным аргументом). Более подробно эти важные для символьных операций функции будут рассмотрены в дальнейшем.

Нетрудно заметить, что Mathematica вычисляет все эти функции как с действительным, так и комплексным аргументом. Аргументом может быть список — тогда функция возвращает список вычисленных значений. Набор элементарных функций функционально полный, то есть отсутствующие в нем функции всегда можно вычислить через имеющиеся.

Комбинирование списков и работа с множествами

Иногда возникает необходимость комбинирования нескольких списков. Для этого используются следующие функции:

Complement [list, listl, list2, ...] — возвращает список list с элементами, которые не содержатся ни в одном из списков listl, Iist2, ...; Intersection [listl, list2,...] (пересечение множеств) —возвращает упорядоченный список элементов, общих для всех списков listi; Join[list1, list2,... ] — объединяет списки в единую цепочку (выполняет конкатенацию). Join может применяться к любому множеству выражений, имеющих один заголовок; Union [listl, Iist2, ...] (объединение множеств) — удаляет повторяющиеся элементы списков и возвращает отсортированный список всех различающихся между собой элементов, принадлежащих любому из данных списков listi. Функция обеспечивает теоретико-множественное объединение списков; Union [list] — возвращает отсортированный вариант списка list, из которого удалены все повторяющиеся элементы.

Приведенные ниже примеры иллюстрируют применение функций комбинирования списков.

Ввод (In)	Вывод (Out)
Complement! {1, 2, 3,4, 5}, {1, а, 2}, {b, с, 5}]	{3,	4}
11={1,2,3,4,5};
12={а,b,3,4,с};
Intersection [11 , 12]	{3,	4}
Join [11, 12]	(1,	2, 3, 4, 5, a, b, 3, 4, c}
Union[{l,2,4,3,2,7,3,5}]	{1,	2, 3, 4, 5, 7}.
Union[{3,2},{!,4}]	(1,	2, 3, 4}
Union[{a,b,c,a},{l,d,3}]	{1,	3, a, b, c, d}

Комбинирование списков позволяет создавать сложные структуры данных из более простых структур. Это может быть полезно при построении очередей, деревьев и иных структурных построений. Кроме того, приведенные функции обеспечивают основные операции со множествами. Функцию Union удобно использовать при решении нелинейных и алгебраических уравнений для удаления повторяющихся решений.

Ряд других функций этого урока перечислен в приложении. В целом можно сделать вывод, что обилие функций работы со списками позволяет решать практически любые задачи, в основе которых лежат манипуляции со списками, стеками и другими родственными типами данных.

Константы

Константы являются типовыми объектами системы, несущими заранее предопределенное численное или символьное значение. Это значение не должно меняться по ходу вычисления документа. К численным константам относятся любые числа, непосредственно используемые в математических выражениях или программных объектах, например процедурах и функциях. Так, числа 1 и 2 в выражении 2*Sin [ 1 ] являются численными константами. Константы-числа не имеют идентификаторов. Идентификатором, в сущности, является само число. Его представление и хранится в памяти.

Имеется также ряд именованных констант, которые можно рассматривать как функции без аргумента, возвращающие заранее заданное значение. Имена констант (и других объектов, например функций и переменных) представляются их идентификаторами — непрерывной строкой символов, отождествляемой с именем. В системе Mathematica большинство идентификаторов имеют естественный математический смысл и начинаются с большой буквы. Например, Е — это основание натурального логарифма.

Используются следующие встроенные именованные константы:

Complexlnf inity — комплексная бесконечность, которая представляет величину с бесконечным модулем и неопределенной комплексной фазой. Degree — число радиан в одном градусе, которое имеет числовое значение Pi/180. Е- основание натурального логарифма с приближенным числовым значением 2 . 71828.... EulerGamma — постоянная Эйлера с числовым значением 0.577216.... GoldenRatio — константа со значением (l+Sqrt[5] ) /2, определяющая деление отрезка по правилу золотого сечения. I — представляет мнимую единицу Sqrt [-1]. Infinity — «положительная» бесконечность (со знаком «минус» дает «отрицательную» бесконечность). Catalan — константа Каталана 0 . 915966.... Pi — число, имеющее значение 3 .14159... и равное отношению длины окружности к ее диаметру.

Константы, имеющие значение, дают его в виде вещественного числа:

{N [Degree], N[E], N[Pi]}

{0.0174533, 2.71828, 3.14159}

{N[EulerGamma],N[GoldenRatio],N[Catalan]}

{0.577216, 1.61803, 0.915966}

Константы в описываемой системе используются вполне естественно, так что от дальнейшего их описания можно воздержаться.

Размерные величины

Mathematica позволяет оперировать с размерными величинами, которые широко используются в физических и химических расчетах. Размерные величины характеризуются не только численными значениями, но и единицами измерения, например Meter (метр), Second (секунда) и т. д. Последние могут стоять в числителе и в знаменателе выражений, представляющих размерные величины:

1 Meter

Meter

5Meter

5 Meter

0.5Second

0.5Second

Между значением размерной величины и единицей измерения знак умножения можно не ставить. Это видно из приведенных выше примеров.

Для облегчения ввода физических констант, представляющих собой размерные величины, в наборе файлов Mathematica можно найти файл PhysicalConstants.nb. При его загрузке появляется дополнительная палитра физических констант, показанная на рис. 3.2.

Для ввода констант достаточно активизировать соответствующую кнопку с нужной константой. Будут введено выражение, задающее константу. Ниже представлены примеры ввода первой и последней констант, содержащихся в палитре, представленных в стандартной форме:

2.99792458000000028'*^8 Meter/ Second

2.99792х108 Meter/ Second

6. 9599 x 108 Meter

6.9599xl08 Meter

Следует отметить, что без острой необходимости применять размерные величины не следует, поскольку они усложняют математические выражения и зачастую не позволяют выполнять с ними символьные преобразования. Рекомендуется нормировать выражения (формулы) так, чтобы результаты их вычисления имели безразмерный вид.

Рис. 3.2. Дополнительная палитра физических констант

Логические функции

Основные логические функции над логическими данными р, q и т. д. задаются следующим образом:

Not[p] или !р Логическое отрицание

And[p, q,...] или р && q &&... Логическое умножение — операция «И»

Or[p,q,...] или р || q | |... Логическое сложение — операция «ИЛИ»

Приведем примеры применения логических операторов и функций.

Ввод (In)	Вывод(Out)
And [True , True , True ]	True
True && True && False	False
Not [True]	False
Not [False]	True
Or [True, True, False]	False
2==2 && 3==3	True
True && True	True
And[l,l,0]	11111 1 0
And[l,l,0]	1 && 1&& 0

Эти примеры показывают, что аргументами логических функций и операндами логических операций должны быть только логические константы True и False или выражения, значения которых представлены ими. Недопустимо использовать численные значения 1 и 0, отождествляя их с логической единицей и логическим нулем. Результатом задания операций с ними будет повтор задания — возможно, в укороченной форме.

Отметим еще ряд логических операторов и функций:

Equal[Ihs, rhs] Greater[х,у] или х > у Возвращает True, если Ihs и rhs тождественны

Greater[xl,x2,x3] или xl > х2 > хЗ Возвращает True, если х оказывается больше у, иначе возвращает False

GreaterEqual[х,у] или х >= у Возвращает True, если xi образуют строго убывающую последовательность, иначе возвращает False

GreaterEqual[xl,х2,хЗ] или xl>= х2 >= хЗ Возвращает True, если х больше или равно у, иначе возвращает False

Negative[х] NonNegative[х] Positive[х] Возвращает True, если xi образуют невозрастающую последовательность, иначе возвращает False

SameQtlhs,rhs] или Ihs === rhs Возвращает True, если х оказывается отрицательным числом, иначе возвращает False

Xor[el, e2,...] Возвращает True, если х — неотрицательное число, иначе возвращает False

Возвращает True, если х — положительное число, иначе возвращает False

Возвращает значение True, если выражение Ihs тождественно rhs, иначе False. В отличие от Equal, сравнивает форму представления операндов, а не их значения

Является логической функцией XOR (исключающее «ИЛИ»). Возвращает True, если нечетное количество из ei имеют значение True, а остальные False. Возвращает False, если четное количество ei имеют значение True, a остальные False

Ниже приводятся примеры использования этих функций.

Ввод (In)	Вывод (Out)
Positive [2-3]	False
Equal [1+2, 4-1]	True
Equal [1+2, 2]	False
Greater [5, 4]	True
Greater [5, 4,3]	True
Greater [5, 4, 9]	False
Less [3,2+3]	True
Positive [2]	True
Negative [-2]	True
Neganbve[2]	False
NonNeganive [ -2 ]	False
NonNegative[2]	True
Xor[ True, True]	False
Xor [False , False]	False
Xor [True, False]	True

Ряд дополнительных логических функций читатель найдет в приложении.

Логические операторы

Логическими принято называть операции, отражающие чисто логическое соответствие между данными. В обиходном языке эти связи выражаются утверждениями типа «да» или «нет». Например, на вопрос «Сын вырос выше отца?» мы можем ответить «да» или «нет». В математике (да и в информатике) принято характеризовать логическое соответствие утверждениями True («Верно», «Истина» или «Да») и False («Неверно», «Ложь» или «Пет»). Слова True и False являются символьными константами, отражающими результаты логических операций и в системе Mathematica.

Для осуществления логических операций используются следующие логические операторы:

Равенство (например, а == b)

! = Неравенство

> Больше (например, b > а)

>= Больше или равно

< Меньше

<= Меньше или равно

Возможны следующие формы применения операторов сравнения:

а == b == с

а != b != с

х < у < z

и т. д.

Результатом вычисления этих выражений является выдача логических значений True или False. Это демонстрируют следующие примеры.

Ввод (In)	Вывод (Out)
2=2	True
a=a	True
a=b	a == b
2=3	False
2<3	True
2>3	False
2!=3	True
2+1==3==4-1	True

Объекты и идентификаторы

В общем случае система Mathematica оперирует с объектами. Под ними подразумеваются математические выражения (ехрг), символы (symbols), строки из символов (strings), упомянутые выше числа различного типа, константы, переменные, графические и звуковые объекты и т. д.

Каждый объект характеризуется своим именем — идентификатором. Это имя должно быть уникальным, то есть единственным. Существуют следующие правила задания имен:

sssss — имя объекта, заданного пользователем; Sssss — имя объекта, входящего в ядро системы; $Sssss — имя системного объекта.

Итак, все объекты (например функции), включенные в ядро, имеют имена (идентификаторы), начинающиеся с большой буквы (например Plus, Sin или Cos). Идентификаторы относящихся к системе объектов начинаются со знака $. Заданные пользователем объекты следует именовать строчными (малыми) буквами. Разумеется, под символами s...s подразумеваются любые буквы и цифры (но не специальные символы, такие как +, -, * и т. д.).

Объекты (чаще всего это функции), встроенные в систему, принято называть внутренними или встроенными. Объекты, которые создает пользователь (в том числе используя внутренние объекты), называют внешними объектами. К ним, в частности, относятся процедуры и функции, составляемые пользователем, которые детально рассматриваются в дальнейшем.

Операции линейной алгебры

Линейная алгебра — один из фундаментальных разделов математики. Он во многом способствовал развитию методов вычислений. Средства линейной алгебры (преобразование матриц, решение систем линейных уравнений и т. д.) широко используются при решении задач механики, электро- и радиотехники и других отраслей науки и техники. В этом разделе мы познакомимся с основным набором средств системы Mathematica, предназначенных для решения задач линейной алгебры.

Оперативная помощь по объекту

Оперативную помощь о назначении какой-либо функции или объекта в ходе работы с системой можно получить, используя следующие обращения:

? Name или Names [ "Name" ] — справка по заданному слову Name; ?? Name — расширенная справка по заданному слову Name; ?Аbс* — перечень всех определений, начинающихся с символов Abc; ©ptions [name] — получение информации об опциях объекта Name.

Примеры получения оперативной справки показаны на рис. 3.5.

Рис. 3.5. Примеры получения оперативной справки

Нетрудно заметить, что есть два уровня комментариев оперативной справки. Так, при обращении ?Sin получено лишь сообщение о назначении функции. Обращение ??Sin дает дополнительную информацию о признаках функции, именуемых ее атрибутами.

Многие встроенные функции защищены от модификации атрибутом Protected. К примеру, нельзя определить новую функцию Sin[x]=x A 2, причем вовсе не потому, что это определение абсурдно (далее мы покажем, что можно снять защиту и переопределить любую функцию даже самым абсурдным образом), а потому, что имя функции защищено указанием атрибута Protected (Защищенное). Позднее мы ознакомимся и с иными атрибутами — под ними подразумеваются определенные свойства объектов.

Операторы и функции

Операторы и функции являются основными кирпичиками в построении математических выражений, которые вычисляются или преобразуются системой Mathematica. Кроме того, это важнейшие элементы языка программирования системы. В данном разделе мы познакомимся с этими объектами.

Основные классы данных

Mathematica оперирует с тремя основными классами данных:

численными данными, представляющими числа различного вида; символьными данными, представляющими символы, тексты и математические выражения (формулы); списками — данными в виде множества однотипных или разнотипных данных.

Каждый из этих классов данных в свою очередь имеет ряд специальных, более частных типов данных. На них мы остановимся более подробно.

Основные понятия линейной алгебры

Массивы, в основном в виде векторов и матриц, широко применяются при решении задач линейной алгебры. Прежде чем перейти к рассмотрению возможностей Mathematica в части решения таких задач, рассмотрим краткие определения, относящиеся к линейной алгебре.

Матрица — прямоугольная двумерная таблица, содержащая m строк и п столбцов элементов, каждый из которых может быть представлен числом, константой, переменной, символьным или математическим выражением (расширительная трактовка матрицы).

Квадратная матрица — матрица, у которой число строк m равно числу столбцов п. Пример квадратной матрицы размером 3x3:

1 2  3

4  5  6

7  8  9

Сингулярная (вырожденная) матрица — квадратная матрица, у которой детерминант (определитель) равен 0. Такая матрица обычно не упрощается при символьных вычислениях. Линейные уравнения с почти сингулярными матрицами могут давать большие погрешности при решении.

Единичная матрица — это квадратная матрица, у которой диагональные элементов равны 1, а остальные элементы равны 0. Ниже представлена единичная матрица размером 4x4: 

		1	0	0	0
		0	1	0	0
E	=	0	0	1	0
		0	0	0	1

Транспонированная матрица — квадратная матрица, у которой столбцы и строки меняются местами. Приведем простой пример.

Исходная матрица:

		a	b	c
A	=	d	e	f
		i	k	l

Транспонированная матрица:

		a	d	i
А т	=	b	e	k
		c	f	l

Обратная матрица — это матрица М -1 , которая, будучи умноженной на исходную квадратную матрицу М, дает единичную матрицу Е.

Ступенчатая форма матрицы соответствует условиям, когда первый ненулевой элемент в каждой строке есть 1 и первый ненулевой элемент каждой строки появляется справа от первого ненулевого элемента в предыдущей строке, то есть все элементы ниже первого ненулевого в строке — нули.

Диагональ матрицы — расположенные диагонально элементы А., матрицы А.
В приведенной ниже матрице элементы диагонали представлены заглавными буквами:

		A	b	c
А	=	d	E	f
		i	k	L

Обычно указанную диагональ называют главной диагональю — для матрицы А, приведенной выше, это диагональ с элементами А, Е и L. Иногда вводят понятия поддиагоналей (элементы d и k) и наддиагоналей (элементы b к f).

Ранг матрицы — наибольший из порядков отличных от нуля миноров квадратной матрицы.

След матрицы — сумма диагональных элементов квадратной матрицы. Определитель матрицы — это многочлен от элементов квадратной матрицы, каждый член которого является произведением п элементов, взятых по одному из каждой строки и каждого столбца со знаком произведения, заданным четностью перестановок:

detА = Сумма a1j(-1)j+1M1<j>

где M <J> — определитель матрицы порядка n-1, полученной из матрицы А вычеркиванием первой строки и j-то столбца. В таком виде определитель (он же детерминант) легко получить в символьных вычислениях. В численных расчетах мы будем подразумевать под определителем численное значение этого многочлена.

Матрица в целой степени — квадратная матрица в степени п (п — целое неотрицательное число), определяемая следующим образом: М° = Е, М 1 = М, М 2 = = М*М,..., Мn = М n-1 -М.

Идемпотентная матрица — матрица, отвечающая условию Р 2 = Р.

Инволютивная матрица — матрица, отвечающая условию I 2 = Е.

Симметрическая матрица — матрица, отвечающая условию А т = А.

Кососимметрическая матрица — матрица, отвечающая условию А т = -А.

Ортогональная матрица — матрица, отвечающая условию А т = А- 1 .

Комплексно-сопряженная матрица — матрица А , полученная из исходной матрицы А заменой ее элементов на комплексно-сопряженные.

Эрмитова матрица — матрица А, удовлетворяющая условию А = А .

Собственный вектор квадратной матрицы А — любой вектор х е V n , х не равно 0, удовлетворяющий уравнению Ах = gx, где g — некоторое число, называемое собственным значением матрицы А.

Характеристический многочлен матрицы — определитель разности этой матрицы и единичной матрицы, умноженный на переменную многочлена — |А - g Е|.

Собственные значения матрицы — корни ее характеристического многочлена.

Норма — обобщенное понятие абсолютной величины числа. Норма трехмерного вектора ||х|| — его длина. Норма матрицы — значение sup(||Ax||/||x||). I-норма матрицы А — число

Матричная форма записи системы линейных уравнений — выражение А-Х = В, где А — матрица коэффициентов системы, X — вектор неизвестных, и В — вектор свободных членов. Один из способов решения такой системы очевиден — X = А -1 В, где А- 1 — обратная матрица.

Переменные

Переменными в математике принято называть именованные объекты, которые могут принимать различные значения, находящиеся в определенном множестве допустимых значений. Подобно этому, переменными в системе Mathematica являются именованные объекты, способные в ходе выполнения документа неоднократно принимать различные значения — как численные, так и символьные. При этом символьные значения переменных, в отличие от обычных языков программирования, могут представлять собой как исполняемые математические выражения ехрг, так и некоторые обобщенные классы функций и объектов. Например, переменная может представлять графический объект, такой как изображение трехмерной поверхности, или звуковой объект, при активизации которого исполняется звук. Значением переменных могут быть также множественные объекты — списки.

Имена переменных называют их идентификаторами. Они должны быть уникальными, то есть не совпадать с именами директив, атрибутов, опций и функций в ядре системы. Имена переменных должны начинаться с буквы. Общеприняты, скажем, имена х и у для функциональной зависимости у (х) или представления графиков, f — для функций. Желательно назначать именам переменных смысловые значения, например xcoordinaate или ycoordinate для координат точки. Все сказанное об идентификаторах объектов справедливо и для идентификаторов переменных, поскольку переменные — распространенные виды объектов.

Особенности применения переменных

В отличие от переменных в математике, каждая переменная в системе Mathematica, как и в любой системе программирования, всегда отождествляется с некоторой физической областью памяти, в которой и хранится значение переменной. Для уменьшения объема памяти применяются различные способы компактного размещения информации. Надо помнить, что и имя переменной занимает определенную область памяти. Распределение памяти под переменные — динамическое. Это означает, что местоположение ячеек памяти и объем памяти под ту или иную переменную не фиксированы, а меняются в ходе выполнения задачи.

Заранее объявлять тип переменной не требуется. Он определяется операцией присваивания переменной некоторого значения. Такой подход упрощает построение программ и естественен при использовании переменных в обычной математической литературе.

Без особых на то указаний переменные в системе Mathematica являются глобальными. Это означает, что после определения переменной ее значение можно изменить в любом месте документа или программы. Переменная появляется как действующий объект только после ее первого определения или задания. Определения переменных выполняются с помощью операции присваивания, вводимой знаком равенства:

var = value

Здесь var — имя переменной, value — ее значение. Ниже представлены основные операции по присваиванию переменным значений:

х = value — переменной х присваивается вычисленное значение value; х = у = value — вычисленное значение value присваивается переменным х и у; x:=value — присваивание переменной х невычисленного значения value; х =. — с переменной х снимается определение. Примеры (комментарий ln[...] опущен):

g = Plot[Sin[x],{x,0,20}] — переменной д присваивается значение в виде графического объекта; у = 1 + х ^ 2— переменной у присваивается символьное значение в виде математического выражения (1 + х ^ 2); z= {1, 2, х, a + b}— переменной z присваивается значение в виде списка, содержащего четыре элемента. Различие в присваивании переменным значений с помощью знаков «=>> и <<:=» иллюстрируют следующие примеры:

а=12;

b=а

12

с:=а

с

12

а=15;

b

12

с

15

Как видите, после первоначальных присваиваний b=а и с: =а обе переменные, b и с, имеют значение 12. Однако после присваивания переменной а нового значения (15) переменная b, которой было присвоено вычисленное значение а, остается равной 12, а переменная с, которой было присвоено невычисленное значение а, становится равной 15.

Особо обратите внимание на то, что возможно снятие с переменной определения с помощью символов «=.» или функции Clear [var].


В символьной математике это очень полезная возможность, поскольку нередко переменные с одним и тем же именем в разных частях программы могут иметь разный смысл и представлять объекты, требующие значительных затрат памяти.

Более того, эти объекты сохраняются даже при использовании команды New при переходе к подготовке нового документа. Поэтому рекомендуется всякий раз удалять определения переменных, как только их использование завершается. Это предотвращает возникновение конфликтов между одноименными переменными и освобождает память.

Переменные могут быть локальными, то есть действующими только в пределах объекта, в котором они объявлены. Таким объектом может быть функция или процедура со списком входных параметров. Такие объекты мы рассмотрим позже.

Оценивание переменных и операции присваивания

Специфику математических выражений в системе Mathematica составляет возможность их оценивания и изменения в соответствии с заложенными в ядро системы правилами математических преобразований. В итоге после изменения значение выражения, которое присваивается переменной, может быть совсем иным, чем до оценивания. Поэтому в целом для определения переменных используют описанные ниже конструкции.

Основная функция Set [ Ihs, rhs ] имеет аналогичные по действию упрощенные операторы:

Ihs = rhs — вычисляет правую часть rhs и присваивает ее значение левой части Ihs. С этого момента Ihs замещается на rhs всюду, где бы этот идентификатор ни появился; {11, 12, ...} = {rl, г2, ...} — вычисляет ri и назначает полученные результаты соответствующим 11. Функция задержанного присваивания SetDelayed[lhs,rhs] может быть заменена аналогичным по действию оператором Ihs : =rhs, который назначает правой части rhs роль отложенного значения левой части Ihs. При этом rhs содержится в невычисленной форме. После этого, когда появляется идентификатор Ihs, он заменяется на значение rhs, вычисляемое каждый раз заново.

При задержанном (отложенном) присваивании вывода нет, тогда как при обычном немедленном присваивании lhs=rhs значение rhs вычисляется немедленно и результат выводится в строку вывода.



Функция присваивания верхнего уровня UpSet [Ihs, rhs] применяется в виде lhs A =rhs. При этом левой части Ihs присваивается значение правой части rhs, причем это значение связывается с символами, которые появляются на первом уровне вложенности в Ihs.

И, наконец, функцию отложенного присваивания верхнего уровня UpSetDelayed[lhs, rhs] может заменить оператор lbs^ :=rhs. При этом величина rhs выполняет роль отложенного значения Ihs, и связывается это присваивание с символами, которые появляются на первом уровне вложенности в Ihs.

Отметим еще одну важную конструкцию SetOptions [s, namel->valuel, name2->value2, . . . ], которая устанавливает для символа s указанные опции, определяемые по умолчанию.

Применение различных типов операций присваивания способствует большей гибкости системы. Различия между этими операциями на первый взгляд несущественны, но они принципиальны, и это станет понятно после более детального знакомства с символьными преобразованиями и приобретения практики работы с системой.

Имеются также системные переменные, значениями которых являются данные о системе и ее работе, например версия применяемой операционной системы, текущая дата, время в данный момент, машинная точность вычислений и т. д. Многие из таких переменных имеют отличительный знак $ перед своим именем. Такие переменные более подробно будут рассматриваться в дальнейшем.

Подстановки

Важное значение в числовых и символьных преобразованиях имеют операции подстановки (rules). Их смысл заключается в замене одного объекта или его части другим объектом или частью другого объекта. Например, часто возникает необходимость вычислить значение математического выражения при замене некоторой переменной ее конкретным численным значением. Для этого достаточно вместо этой переменной подставить нужное численное значение.

Куда менее тривиальной является замена переменной ее символьным значением в виде математического выражения. При этом исходное выражение может в ходе решения задачи превратиться в совершенно новое выражение, поскольку после подстановки система может провести над исходным выражением достаточно сложные математические преобразования. Говорят, что в этом случае ячейка, содержащая выражение (а точнее — само выражение), оценивается и изменяется по ходу решения задачи. Операции подстановки обычно вводятся с помощью комбинации символов «/ .»:

ехрг / . х -> value — в выражение ехрг вместо переменной х подставляется ее значение value; ехрг /. {х -> xvalue,. у -> yvalue} — в выражение ехрг вместо переменных х и у подставляются их значения xvalue и yvalue.

Примеры:

l+x^3/.x->l+z

1 + (1+ z)3

х^2+2*х+3/.х->2

11

Обратите внимание на то, что в результате подстановки в первом примере вместо переменной х оказалось математическое выражение (1 + z). Второй пример иллюстрирует подстановку на место переменной х ее численного значения.

В целом для операций подстановок используют следующие обозначения:

Ihs -> rhs — прямая подстановка Ihs в rhs; Ihs :> rhs — отложенная подстановка (RuleDelayed), которая преобразует Ihs в rhs, вычисляя rhs не сразу, а только при использовании правила подстановки.

Ниже приведены еще два примера на использование операций подстановки:

р:=1+х^2+3*х^3

р/.х->1+у

1+ (1 + у)2+3 (1 + у)3

{f[1],f[2],f[3]}/.f[n_]->n^2

{1, 4, 9}

f[n_]:=n^2

f[4]+f[y]+f[x+y]

16+y2+(x+y)2

В первом примере подстановка произведена в математическое выражение, а во втором — в список.

Подстановки — мощный и необычайно гибкий инструмент системы Mothematica. С их помощью можно задать даже новые математические закономерности и произвольные соотношения (к примеру, можно задать абсурдное правило, что 2 + 2 = 5). Эти необычные возможности мы рассмотрим в дальнейшем.

Получение данных об объектах

Различные объекты системы будут более подробно описаны в дальнейшем по мере знакомства с системой. Полный список объектов, заданных в ядре системы, легко получить, используя команду ? * (ниже приведены лишь начало и конец этого списка):

?*

Abort

AbortProtect

Above

Abs

AbsoluteDashing

AbsolutePointSize

$Version

$VersionNumber

Можно также получить список всех определений на заданную букву, используя команду ?S*, где S — любая буква латинского алфавита. Ниже дан пример вывода всех определений ядра на букву U:

?U*

UnAlias Unevaluated Update

Underflow Uninstall UpperCaseQ

Underoverscript Union UpSet

UnderoverscriptBox Unique UpSetDelayed

Underscript Unprotect Upvalues

UnderscriptBox UnsameQ Using

Unequal Unset

Аналогичные возможности предоставляет функция Names ["S"], например, Names ["А*"] дает список всех ключевых слов, начинающихся с символа «А». Наконец, командой ?Name можно вывести справку по любому определению с именем Name. Например, после выполнения команды

?Abs

Abs[z] gives the absolute

value of the real or complex number z.

становится ясно, что идентификатор Abs задает функцию Abs [ z ] для вычисления абсолютного значения комплексного числа.

С помощью выражения ?Name можно проверить, является имя объекта Name уникальным или оно уже использовано в системе:

?sin

Information::notfound : Symbol sin not found.

?Sin

Sin[z] gives the sine of z.

В первом случае ясно, что имя sin не использовано, а во втором случае мы видим, что имя Sin уже зарезервировано — это функция вычисления синуса. В задачу этой книги не входит описание всех без исключения определений ядра системы, так что указанные выше приемы весьма полезны, если вы обнаружили функцию, по которой нет информации.

Всякий объект перед использованием должен быть определен (задан). Внутренние объекты уже заданы в ядре. Объекты пользователя последний задает в текстах своих документов (notebooks).

Кроме того, некоторая совокупность новых внешних объектов может храниться в пакетах расширения, большой набор которых включен в поставку системы. Пользователь может и сам готовить пакеты расширений, обеспечивающие адаптацию системы к решению интересующего его класса задач. Пакеты расширений представлены файлами с расширением .т.

Работа с объектами

В этом разделе мы познакомимся с понятием объектов и научимся работать с ними. Объект — понятие обобщенное. Под ним может подразумеваться оператор или функция, рисунок (графический объект) и т. д. Объекты могут иметь ряд свойств, определяющих их назначение и поведение.

Работа со списками и массивами

Списки относятся к данным множественного типа. Они имеют большое значение при обработке массивов данных и служат основой для создания векторов и матриц. В этом разделе мы познакомимся со свойствами списков, их созданием (генерацией) и использованием.

Работа со списком в стеке

Списки можно представить в виде особой структуры данных — стека. Стек — это структура данных, напоминающая стопку тарелок в шкафу. При этом тарелки играют роль данных. Очередную тарелку можно положить только сверху (на вершину стека). На дне стека лежит первая помещенная в него тарелка. Стек подчиняется следующему правилу: последнее введенное значение извлекается первым, а первое введенное значение извлекается последним. Стек относится к системам хранения данных динамического типа, его размеры непрерывно меняются по ходу вычислений. Стек может быть пустым, если из него извлечены все данные.

Система Mathematica предоставляет широкие возможности для операций со стеками:

Drop [list, n] — возвращает список list, из которого удалены первые п элементов; Drop [list, -n] — возвращает список list с отброшенными последними п элементами; Drop [list, {n}] — возвращает список list без n-го элемента; Drop [list, {m, n}] — возвращает список list с отброшенными элементами от m-го до п-го; Fold[f, x, list] — возвращает последний элемент из FoldList [f,x, list]; Last [list] — возвращает последний элемент списка list; Rest [list] — возвращает список с уничтоженным первым элементом; Take [list, n] — возвращает первые п элементов списка list; Take [list, -n] — возвращает последние п элементов списка list; Take [list, {m, n}] — возвращает элементы списка с порядковыми номерами от m до п.

Следующие примеры поясняют работу со стеком.

Ввод (In)						Вывод(Out)
Drop[{l	,2	,3	,4	,5},	2]	{3,	4,	5}
Drop [ { 1	,2	,3	,4	,5},	-2]	{1,	2,	3}
Drop [ { a	,b	,c	,d	,e>,	{2,4}]	(a,	e}
Last[{l	,2	,3	,4	,5}]		5
Rest[{l	,2	,3	,4	,5}]		{2,	3,	4, 5}
Take[{l	,2	,3	,4	,5},	2]	(1,	2}
Take [ { 1	,2	,a	,b	,c},	-2]	{b,	c}
Take [ { 1	,2	,3	,4	,5},	{2,4}]	{2,	3,	4}

Тривиальная процедура общения со стеком (ввести/вывести данные) ограничивает возможности стековых операций. Из житейского опыта мы знаем, что, проявив настойчивость, можно вставить тарелку и в середину стопки. Mathematica предоставляет ряд расширенных возможностей для работы со списками, выходящих за рамки обычных стековых операций.

Так, например, для расширения списка путем включения в него новых элементов используются следующие функции:

Append [list, element] — добавляет элемент в конец списка; PreoendTlist.element1 — добавляет элемент в начало списка: Insert [list, element, n] — вставляет элемент в позицию п (отсчет пози-ций.ведется с начала списка, а если число п отрицательное — то с конца). Данной функцией можно включать элемент в несколько позиций, указав каждую в фигурных скобках, взяв все перечисление в еще одни фигурные скобки и использовав его вместо п. При этом надо учитывать, что все позиции включаемых элементов определяются одновременно до начала расширения списка. Следующие примеры иллюстрируют применение этих функций.

Ввод (In)	Вывод(Out)
1={1,2,3}		(1,	2,	3}
Append[l,e]		(1,	2,	3,	e}
Prepend[l,e]		{e,	1,	2,	3}
Insert[l,e,2]		{1,	e,	2,	3}
L={1, 2, 3, 4	, 5}	{1,	2,	3,	4, 5}
Insert [L, e,	-5]	(1,	e,	2,	3, 4, 5}
Insert [L, e,	{{1},{5}}]	(e,	1,	2,	3, 4, e, 5}

Обратите внимание на то, что в данном случае элементы списка — числа, тогда как вставляемый элемент имеет символьное значение е.

Следует отметить, что описанные для стека функции Drop и Rest позволяют удалить из списка последний или первый элемент. Функция Delete [list, i] позволяет удалить из списка произвольный i-й элемент. Если i>0, то отсчет удаленного элемента идет с начала списка, а если i<0 — с конца:

L:={1,2,3,4,5}

{Delete[L,l],Delete[L,3],Delete[L,5]}

{{2, 3, 4, 5}, {1, 2, 4, 5}, {1, 2, 3, 4}}



{Delete[L,-2],Delete[L,-5]}

{{1, 2, 3, 5}, (2, 3, 4, 5}}

Delete[{l,2,3,{a,b,c},4,5},2]

{1, 3, {a, b, c}, 4, 5}

Если элементом списка является список, то он фигурирует как один элемент. Можно, однако, удалить избранный элемент из элемента списка, указав в фигурных скобках вместо i номер элемента списка во внешнем списке и номер удаляемого элемента во внутреннем списке. Это иллюстрируют следующие примеры:

Delete[(1,2,3,{а,Ь,с},4,5},{4,3}]

{1, 2, 3, {а, b}, 4, 5}

Delete[{1,2,3,{а, b, с},4,5},{4,1}]

{1, 2, 3, {b, с}, 4, 5}

Наконец, с помощью функции Delete можно удалить несколько элементов списка, указав каждый из них в фигурных скобках и оформив это указание также в фигурных скобках:

Delete [ {1,2,3, {a, b, c} , 4, 5}, {{2}, {4} ,{ 5}}]

{1, 3, 5}

Следует иметь в виду, что некоторые функции удаляют в списках определенные элементы. Этот вопрос будет рассмотрен ниже.

Решение систем линейных уравнений

Приведем также примеры на решение систем линейных уравнений матричными методами. В первом из них решение выполняется в символьном виде на основании формулы X = А -1 В, где А — матрица коэффициентов системы линейных уравнений, В — вектор свободных членов. Для перемножения используется функция Dot, а для инвертирования матрицы — функция Inverse:

A:={{a,b},{c,d}}

B:={e,f}

X:=Dot[Inverse[A],B]

X

{-de/(bc+ad) -bf/(bc+ad)- ce/(bc+ad) -af/(bc+ad)}

Во втором примере для решения системы линейных уравнений используется функция LinearSolve:

LinearSolve[{{l,2},{3,4}},{7,9}]

{-5, 6}

Нередко, например в электротехнических расчетах, встречается необходимость решения систем линейных уравнений с комплексными элементами. Все описанные выше функции обеспечивают работу с комплексными числами. Следующий пример иллюстрирует решение системы линейных уравнений с комплексными данными:

А={ U+2I,2+3I},{3+4I,4+5I}}

{{1+21, 2 + 31}, {3 + 41, 4+ 51}}

В={21,3}

{21,3} X=LinearSolve[А,В]

{1/4-41, 11I/4}

Число матричных функций в системе Mathematica 3/4 ограничено разумным минимумом, позволяющим реализовать множество других, более сложных матричных функций и преобразований. Их можно найти в пакетах расширения системы, посвященных линейной алгебре.

Символьные данные и строки

Символьные данные в общем случае могут быть отдельными символами (например a, b,..., z), строками (strings) и математическими выражениями ехрг (от expression — выражение), представленными в символьном виде.

Символьные строки задаются цепочкой символов в кавычках, например "sssss". В них используются следующие управляющие символы для строчных объектов:

\n— новая строка (line feed); \ t — табуляция.

Это иллюстрируется следующими примерами:

"Hello my friend!"

Hello my friend!

"Hello\nmy\nfriend!"

Hello

my

friend!

"Hello\tmy\tfriend!"

Hello my friend;

Следует помнить, что управляющие символы не печатаются принтером и не отображаются дисплеем, а лишь заставляют эти устройства вывода выполнять определенные действия. Mathematica имеет множество функций для работы со строками, которые будут описаны в дальнейшем.

Создание массивов

Совокупность данных образует массив (Array). Массивы могут быть одномерными (один список), двумерными и многомерными (два и более списка). Одномерные массивы в математике называют векторами, двумерные — матрицами. В общем случае массив характеризуется размерностью (числом измерений) и размером — произведением числа элементов по всем размерностям. Mathematica позволяет создавать многомерные массивы — число элементов в них ограничено лишь объемом памяти компьютера.

Для задания массивов используются следующие функции:

Array [ f, n] — генерирует список длиной п с элементами f [ 1 ], f [ 2 ], ..., f[n]; Array [f, {nl, n2, ...}] — генерирует массив размером n1x n2 x... в виде вложенных списков с элементами f [ i I, i2,...] (аргумент функции i k меняется от 1 до nk); Array[f, dims, origin] — генерирует список с размерностью dims, используя спецификацию индекса origin; Array [f, dims, origin, h] — использует заголовок h, а не List, для каждого уровня массива.

Далее приводятся примеры задания массивов и их вывода.

Ввод (In)	Вывод (Out)
Y : =Array [Exp , 4 ] Y	{e,	e 2 ,	e 3 ,	e 4 }
N[Y]			{2.	71828,	7.	38906,	20.0855, 54	.5982}
Array[f,{3	,	3}]	{{f	[1,	1],	f	[1, 2]	{	f[l,	3]},	{f[2, 1], f[2, 2],
			{[2	, 3]	},	{f	[3, 1]	{	f[3,	2], f	[3, 3] }}
Array [Sin,	3	,0]	{0,	Sin	[1]	, Sin[2]	}
Array [Sin,	4	,l,Plus]	Sin	[1]	+ Sin	[2] +	Sin[3]	+ Sin	[4]
Array[f ,5,	2	,2]	2[f	[2],	f [	3]	, f[4]	{	f [5]	, f[6]	]

Списки и их свойства

Часто математические или иные объекты содержат множество данных, которые желательно объединять под общим именем. Например, под объектом с именем М можно подразумевать квадратную матрицу размером 10x10 с общим числом элементов, равным 100. Человека с именем Victor, например, можно характеризовать целым списком разных данных — символьными фамилией, именем и отчеством, целочисленным годом рождения, вещественным ростом, объемом груди и т. д.

Для объединения данных могут использоваться списки (list). Mathematica имеет обширные возможности работы с объектами-списками, содержащими не только однотипные, но и разнотипные элементы. В частности, элементами списков могут быть числа, константы, переменные, выражения и даже сами списки. Списки используются для конструирования более частных типов данных — массивов, матриц и векторов [87].

На языке данной системы список — это совокупность произвольных данных, указанных в фигурных скобках, например: {1, 4, 2, 7, 9} или {а, Ь, с, d, e, sin[x], ln[y], "string"}

Возможно задание списков в списке, например, так:

{{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}

Такой список представляет матрицу

1  2  3

4  5  6

7  8  9

Однако, чтобы вывести список в такой матричной форме, надо использовать после списка выражение //MatrixForm (рис. 3.7).

Рис. 3.7. Примеры задания и вывода матрицы

На рис. 3.7 показан еще один способ задания списка или матрицы — с помощью функции List:

List [a, b, с,...] — создает список {а, b,, с,...}; List [ {а,b, с,...}, {d,e, f,...}, {i, k, 1,...} ] — создает список — матрицу { {a,b, с,...}, {d,e, f,...}, {i, k, 1,...} }.

Списки можно составлять, непосредственно задавая объекты в соответствии с описанным синтаксисом. Однако можно и генерировать некоторые виды списков, таких как таблицы. Списки могут быть объектами присваивания переменным, например

V:={1, 2, 3, 4, 5}

Списки характеризуются размером, который представляет собой произведение числа элементов списков по каждому направлению (размерности). Например, одномерный список является вектором и характеризуется числом элементов по единственному направлению. При этом вектор может быть вектором-строкой или вектором-столбцом. Двумерный список представляет матрицу, имеющую m строк и n столбцов. Ее размер равен mxn. Если m=n, то матрица называется квадратной. Трехмерный список можно представить в виде параллелепипеда, содержащего mxnxp элементов. Списки большей размерности трудно наглядно представить, но они вполне возможны. Напомним, что имена векторов и матриц в данной книге обозначены жирными символами, например, V для вектора и М для матрицы.

Списки и массивы

Наиболее общим видом сложных данных в системе являются списки (lists). Списки представляют собой совокупности однотипных или разнотипных данных, сгруппированных с помощью фигурных скобок:

{ 1 , 2 , 3 } — список из трех целых чисел; { а , b , с } — список из трех символьных данных; {1, а, x^ 2} — список из разнотипных данных; {{a,b},{c,d}} — список, эквивалентный матрице

a b

c     d

{х^2+у^2, 2*Sin [x] } — список из двух математических выражений.

Как видно из этих примеров, элементы списков размещаются в фигурных скобках — открывающей { и закрывающей } . Списки могут быть с вложениями из списков — так получаются многоуровневые списки (двухуровневый список дает матрицу). Позже свойства и возможности списков будут рассмотрены детально. С помощью списков представляются множественные данные — массивы.

Средства диагностики и сообщения об ошибках

Средства диагностики органично входят во все программные модули системы Mathematica, созданные профессионально. Благодаря этому система обнаруживает неточные действия пользователя, например синтаксические ошибки при вводе идентификаторов функций и команд, неправильное использование типов данных, применение недопустимых операций (вроде злосчастного деления на ноль) и т. д. Всякий раз, когда ошибочное действие обнаружено, система выдает сообщение об ошибке в следующем виде:

Тип::Метка%Диагностика:Сообщение

Эти сообщения появляются в отдельных неактивных ячейках. Тип указывает на тип ошибки, например, General — ошибка общего вида, Syntax — синтаксическая ошибка, Arg — ошибка задания аргумента и т. д. Метка указывает место ошибки в списке ошибок данного типа, а Диагностика указывает (увы, не всегда...) на ошибочное выражение. Сообщение обычно раскрывает суть ошибки.

Допустим, мы пытаемся вычислить значение экспоненциальной функции, указав ошибочно аргумент 2,3 с разделительной запятой вместо точки. Вот как Mathematica отреагирует на такую попытку (рис. 3.6, первый пример).

Рис. 3.6. Примеры выполнения «ошибочных» операций

Итак, ясно, что произошла ошибка задания аргумента — функция Ехр должна иметь только один аргумент, а число 2,2 система воспринимает как два аргумента, разделенные запятой. Вот еще один пример — вроде бы ошибочно заданы круглые скобки в выражении N (Ехр (2) ). Mathematica 3 в этом случае дала бы два предупреждающих сообщения:

Syntax::bktwrn : "Ехр(2)" should probably be "Ехр[2]".

Syntax::bktwrn : "N(Exp(2)l" should probably be "N[Exp(2)]".

2ExpN

Однако Mathematica 4 в подобных случаях дает допустимую для данной системы форму представления введенного выражения. Тем не менее, надо отметить, что сообщения об ошибках системы Mathematica дают не только указания о самом по себе факте наличия ошибки, но и сообщают о том, что надо сделать для ее исправления.

Как видно из сведений о подготовке пакетов расширения, сообщения об ошибках и иные сообщения (в том числе информационные) заданы в их структуре.
Насколько эти сообщения точны и как они предугадывают возможные ошибки — это уже зависит от опыта программиста, готовящего программные модули.

Включение и выключение сообщений об ошибках

Опытный пользователь нередко способен опознать ошибки и без слишком назойливых сообщений о них. Например, он может судить о своей промашке просто по отказу системы выполнить вычисление и по повтору выражения в строке вывода (см. примеры выше). Кроме того, часть сообщений носит предупреждающий характер и на первых порах может игнорироваться.

Для отключения сообщений об ошибках служит ключ

Off[Function::tag]

Например, отключим сообщение об ошибках у функции Ехр:

Off[Exp::argx]

Ехр[2,2]

Ехр[2,2]

Ехр[2]

Е2

N[Exp[2]]

7.38906

Для включения сообщения об ошибках используется ключ

On[Function::tag]

Например, для возобновления выдачи ошибок у функции Ехр надо исполнить команду

On[Exp::argx]

К сожалению, диагностика ошибок не способна опознать ошибки, имеющие формально правильный синтаксис. Чаще всего эти ошибки связаны с неверным описанием алгоритма вычислений. Например, если пользователь в математическом выражении вместо Sin [х] записал Cos [х], то эта грубая ошибка никак не будет распознана системой, поскольку синтаксически вызов функции Cos [х] записан безупречно. Часто пользователи путают идентификаторы переменных. Естественно, что ответственность за такие ситуации целиком лежит на пользователе — программисте.

Типы данных

Основные классы данных Выражения Списки и массивы Объекты и идентификаторы Функции, опции, атрибуты и директивы Подстановки Функции линейной алгебры

С этого урока начинается серьезное освоение математических возможностей систем Mathematica 3 и 4. Мы изучим основные типы данных, операторов, функций и объектов, с которыми может работать система Mathematica 3/4, а попутно познакомимся и с некоторыми простыми операциями ввода данных и их обработки.

Встроенные функции

Важнейшим объектом любой компьютерной математической системы является функция. Она отражает зависимость некоторой величины от одного или нескольких аргументов. Например, функция sin(x) дает зависимость синуса х от величины аргумента х при изменении последнего от -°° до +°°.

Признаком функции является возврат результата выполняемого ею действия. Характер результата будет зависеть от смысла функции, который нередко явно указывается ее именем — идентификатором. Например, функция Digitslnteger [n] возвращает число десятичных цифр десятичного целого числа. Это ясно из прямого перевода имени функции — слово Digitslnteger говорит о том, что она возвращает число цифр целого числа. Подобные смысловые имена задаются для большинства функций системы Mathematica и облегчают их запоминание.

Понятие функции в системе Mathematica существенно расширено — функции могут возвращать графические и даже звуковые объекты. Здесь мы, однако, остановимся на общепринятом в программировании понятии функций, возвращающих в ответ на обращения к ним численные или символьные значения.

Функции могут входить в состав математических выражений. Обычно они имеют один или несколько параметров, указываемых в квадратных скобках. Если параметров несколько, то в квадратных скобках указывается список параметров, разделенных запятыми. В общем случае параметрами могут быть списки. Наконец, в состав функций могут входить опции, указанные своим именем и (после знака ->) значением. Для обозначения положительной бесконечности используется символ Infinity. Целочисленные функции имеют в своем имени слово Integer.

В ядро систем Mathematica 3/4 входит множество встроенных функций, то есть функций, готовых к немедленному использованию без какого-либо предварительного объявления. Таких функций многие сотни. Среди них различные арифметические функции, тригонометрические и гиперболические функции, специальные математические функции и т. д. Мы рассмотрим их в дальнейшем.

Основные арифметические функции

Для выполнения арифметических действий в системах Mathematica 3/4 определены следующие арифметические функции:

Divide [х, у] — возвращает результат деления х на у эквивалентно выражению х у ^ -1; Plus[x, у,...] — возвращает сумму элементов списка; PowerModta, b, n] — возвращает Mod[a ^ b, n]. Для b<0 возвращает инверсию остатка; Times [х, у,...] — возвращает произведение аргументов х*у*...; Mod [m, n] — возвращает остаток от деления m на п. Результат имеет такой же знак, как п. Ниже представлены примеры применения арифметических функций.

Ввод (In)	Вывод (Out)
Divide [1. ,3]	0.333333
Mod [123, 20]	3
Mod [123, -20]	-17
Mod[-123,20]	17
Plus[2,3,4]	9
Times [2, 3,4]	24

Для обмена значениями переменных х и у можно использовать выражение {х,у}={у,х}

Пример обмена переменных значениями:

а=1;b=2;

{а,b}={b,а};

{а,b}

{2, 1}

Следующие функции служат для приведения вещественных чисел к ближайшим целым по определенным правилам:

Ceiling [х] — возвращает значение наименьшего целого числа, большего или равного х; Floor [х] — возвращает наибольшее целое число, не превышающее данного х; Quotient [n, m] — возвращает целое значение n/m, определяемое как Floor[n/m]; Round [х] — округляет х до ближайшего целого. Хотя аргументами этих функций указано значение х, под ним можно понимать список вещественных чисел. Следующие примеры поясняют это и наглядно иллюстрируют правила приведения к целым числам.

Ввод (In)	Вывод (Out)
Ceiling [{-5. 9, -5..1, 5, 5.1, 5.9}]	{-5, -5, 5, б, 6}
Floor [{-5. 9, -5.1,, 5, 5.1, 5.9}]	{-6, -6, 5, 5, 5}
Round[{-5.9, -5.1,, 5, 5.1, 5.9}]	{-6, -5, 5, 5, 6}

Ряд функций обеспечивает нахождение делителей целых чисел и наименьшего общего -кратного:

Divisors [n] — возвращает список целочисленных делителей числа п; DivisorSigma [k, n] — возвращает сумму &-х степеней положительных делителей числа п; ExtendedGCD [n, m] — возвращает расширенный наибольший общий делитель целых чисел пит; GCD [nl,n2,...] — возвращает наибольший общий делитель целых чисел ni; LCM[nl, n2,...] — возвращает наименьшее общее кратное целых чисел ni. Ниже представлены примеры применения этих функций.

Ввод (In)	Вывод (Out)
LCM[124,12,6]	372
GCD [144, 12, 6]	6
Divisors [123]	{1,3,41,123}
DivisorSigma [17,3]	129140164
ExtendedGCD [144,12]	{12, {0,1}}

К целочисленным функциям можно отнести также функции вычисления факториала и двойного факториала:

Factorial [n] или n! — возвращает значение факториала числа n (n!=n* (n-1) *...*3*2*1, причем 0 !=1 и 1 !=1); Factorial2 [n] или n! ! — возвращает значение двойного факториала числа п, равное п* (n-2) * (n-4) *...«%» Ниже представлены примеры вычисления факториалов.

Ввод (In)	Вывод (Out)
Factorial [10]	3628800
20!	2432902008176640000
10!!	3840
20!//N	2.4329Х10 18

Mathematica способна вычислять факториалы больших чисел. Практически мгновенно (даже на компьютере с 486-м процессором) вычисляются значения до 1000!, хотя результат при этом занимает несколько страниц на экране дисплея. Можно вычислить даже 10000!, но для этого потребуется время до нескольких минут (зависит от типа компьютера). Обратите внимание на то, что управляющий символ //N за выражением дает вывод (аппроксимацию) в форме научной нотации.

Следующие функции служат для получения простых чисел и некоторых их характеристик:

Prime [n] — возвращает п-е простое число. Например, Prime [5] возвращает пятое простое число — 11. Всего лишь доли секунды требуются системе для вычисления миллиардного простого числа: Рг1те[10 Л 9] дает 22801763489; PrimePi [x] — возвращает количество простых чисел, не превышающих х. Например, PrimePi [10] возвращает 4; Partitions? [n] — возвращает числор(п) неупорядоченных разбиений целого числа п. Например, Partitions? [10] возвращает 42; PartitionsQ [n] — возвращает q(n) — число разбиений с неравными частями для целого числа п. Например, PartitionsQ [15] возвращает 27. Эти функции полезны при решении задач теории чисел.

Функции генерации случайных чисел

Для реализации статистических методов моделирования используются случайные числа.


Система имеет генератор псевдослучайных чисел, доступ к которому обеспечивают следующие функции:

Random [ ] — возвращает равномерно распределенное псевдослучайное число типа Real в интервале от 0 до 1; Random [type, range] — дает псевдослучайное число указанного типа type, лежащее в указанном интервале range. К возможным типам относятся Integer, Real и Complex. По умолчанию принят интервал от 0 до 1. Можно задать интервал явно в виде {min, max}; спецификация интервала в виде max эквивалентна {0, max}; SeedRandom[n] — сбрасывает (устанавливает в начальное состояйие) генератор случайных чисел, используя целое п как начальное число; SeedRandom [ ] — устанавливает генератор, используя в качестве начального числа текущее время. Хотя генерируемые числа не являются строго случайными, их количество в повторяющейся последовательности очень велико. Использование специальной установки начального состояния генератора, например по времени дня, делает повторение последовательности практически невозможным.

Для проверки равномерности распределения большого массива случайных чисел можно задать с их помощью случайные координаты и затем построить точки, соответствующие координатам (х, у). Рисунок 3.4 наглядно показывает, как это делается для массива из 10 000 случайных точек. О равномерности распределения случайных чисел говорит равномерность распределения плотности точек на графике.



Рис. 3.4. Графическая иллюстрация распределения точек со случайными координатами (х, у)

Возможно, читателю не сразу понятны графические средства, использованные в документе, показанном на рис. 3.4. Это не беда — в последующих уроках они будут описаны довольно подробно.

Функции выявления погрешностей и анализа структуры чисел

Следующие функции, опции и директивы используются, в основном, для выявления погрешностей вычислений и уточнения структуры чисел:

Accuracy [х] — возвращает количество десятичных цифр справа от десятичной точки числа х; EvenQ [expr] — возвращает значение True, если expr есть четное число, и False — в противном случае; IntegerDigits [n] — возвращает список десятичных цифр целого числа n; IntegerDigits [n,b] — возвращает список цифр целого числа п в записи по основанию b; IntegerDigits [n, b, k] — возвращает список длиной k, содержащий самые младшие (наименьшие) значащие цифры в n; Precision [x] — возвращает количество точных знаков в числе х. Поясним применение этих функций следующими примерами.

Ввод (In)	Вывод(Out)
Accuracy [123 . 456]	14
EvenQ [2*3+2]	True
EvenQ [2*3+3]	False
IntegerDigits [12345]	{1, 2,3, 4, 5}
IntegerDigits [12345, 16]	{3, 0,3, 15}
IntegerDigits [12352 , 16]	{3, 0,4, 0}
IntegerDigits [12352 ,2]	{1,1,0,0,0,0,0,0,1,0,0,0,0,0,0}
Precision [123. 452]	16

Функциями Accuracy и Precision возвращаются значения, установленные в последний раз или по умолчанию при первой загрузке системы.

Mathematical имеет обширный набор арифметических операторов и функций, достаточный для решения задач теории чисел и выполнения практически любых арифметических вычислений. Многие более специальные целочисленные функции будут рассмотрены в дальнейшем, по мере описания системы.

Выделение элементов списков

Для выделения элементов списка list используются двойные квадратные скобки:

list [ [i] ] — выделяет i-й элемент списка; list [ [ { i, j , --.}]] — выделяет i-й, j-й и т. д. элементы списка.

Ниже приведены примеры выделения элементов списков.

Пример	Комментарий
11:={1,2,3,4,5)	Задание исходного списка 11
11[[3]]	Выделение третьего элемента
3
11[[{1,2,5}]]	Выделение первого, второго и пятого элементов
(1, 2, 5}
12={{1,2,3},{4,5,6}}	Задание сдвоенного (двумерного) списка
{{1, 2, 3}, {4, 5, 6}}
TableForm[12]	Вывод сдвоенного списка в табличной форме
1 2 3
4 5 6
L2[[2,3]]	Выделение элемента сдвоенного списка
6

Для выделения заданного z'-ro элемента списка list используется также функция Part [list, i]. При i>0 отсчет номеров элементов идет с начала списка, а при i<0 — с его конца. Это правило поясняют следующие примеры:

L:={l,2,3,a,b,c}

{Part[L,2],Part[L,5],Part[L,6]}

{2, b, с}

{Part[L,-2],Part[L,-5],Part[L,2]}

{b, 2, 2}

Функция Part может использоваться для выбора заданного элемента выражения из списка. В этом случае вместо i надо указать три числа — номер выражения как элемента списка, уровень выражения и порядковый номер извлекаемого из

выражения объекта. Показанные на рис. 3.8 примеры иллюстрируют работу со списком, последним (четвертым) элементом которого является математическое выражение.

Рис. 3.8. Примеры выделения элементов выражения

Обратите внимание на то, что в последнем примере неверно задан уровень выражения — использованное выражение имеет только один (первый) уровень. Поэтому задание второго уровня вызывает появление сообщения об ошибке.

Функция Select используется для выделения элементов списка, удовлетворяющих заданному критерию:

Select [list, crit] — выбирает все элементы ei списка list, для которых функция критерия crit [ei] имеет значение True; Select [list, crit, n] — выбирает первые п элементов, для которых critfei] есть True.

Ниже представлены примеры применения этой функции:

Select[{1,а,2,b,3,c},NumberQ]

{1, 2, 3}

Select[{l,a,2,b,3,c),NumberQ,2]

{1, 2}

Select[{l,a,2,b,3,c},PrimeQ]

{2, 3}

 

Выражения

Выражения в системе Mathematica обычно ассоциируются с математическими формулами, как показано в следующей таблице.

Запись на языке Mathematica	Обычная математическая запись
2*Sin[x]	2*sin(x)
2 Sin[x]	2*sin(x)
(а +b^2 + с^З) / (3*d - 4*e)	(a + b 2 +с 3 )/(3d-4е)
sqrt(2)	Кореннь из 2
Integrate [Sin [x] , х]	Интеграл sin(x) dx

Для записи математических выражений используются как операторы, так и функции. Их особенности будут рассмотрены несколько позже. А пока сразу отметим некоторые тонкости синтаксиса системы, используемого при записи арифметических операций:

знак умножения может быть заменен пробелом; встроенные функции начинаются с большой буквы и обычно повторяют свое общепринятое математическое обозначение (за исключением тех, в названии которых есть греческие буквы — они воспроизводятся латинскими буквами по звучанию соответствующих греческих букв); круглые скобки () используются для выделения частей выражений и задания последовательности их вычисления; параметры функций задаются в квадратных скобках [ ]; фигурные скобки {} используются при задании списков.

Новые системы Mathematica 3/4 обладают обширными возможностями по заданию форматов записи математических выражений при их выводе на экран или принтер, а также при вводе с клавиатуры. Они будут рассмотрены в дальнейшем.

Вывод элементов списков

Для вывода элементов списка используются следующие функции:

MatrixFormflist] — выводит список в форме массива (матрицы); TableForm [list] — выполняет вывод элементов списка list в виде таблицы.

С этими функциями используются следующие опции:

TableAlignments — указывает, каким образом должно выравниваться содержимое списка в каждой размерности (слева, по центру или справа); TableDepth — устанавливает максимальное количество уровней, выводимых в табличном или матричном формате; TableDirections — указывает, как следует располагать последовательные (соседние) размерности — в виде строк или столбцов; TableHeadings — задает подписи (labels) для каждой размерности таблицы или матрицы; TableSpacing — устанавливает количество пробелов, которое следует оставлять между соседними строками или столбцами.

Обратите внимание на то, что эти опции используются как для функции TableForm, так и для функции MatrixForm, используемой для вывода матриц. Вообще, векторы и матрицы являются разновидностью списков. На рис. 3.9 поясняется использование функций MatrixForm и TableForm на примере вывода списка.

Рис. 3.9. Примеры вывода списка в матричной и табличной формах

Дополнительные возможности функции TableForm демонстрирует рис. 3.10. Здесь особенно полезно отметить возможность выравнивания данных в таблицах по левому и правому краям, а также по середине.

В большинстве случаев опции для функций MatrixForm и TableForm не используются. Точнее, они установлены по умолчанию. Проверить, какие опции использованы, можно, например, следующим образом:

Options[MatrixForm]

{TableAlignments -> Automatic, TableDepth-> со, TableDirections -> Column,

TableHeadings->None, TableSpacing-> Automatic}

Options[TableForm]

{TableAlignments -> Automatic, TableDepth ->бесконечность, TableDirections -> Column,

TableHeadings -» None, TableSpacing-> Automatic}

Рис. 3.10. Примеры вывода списка в табличной форме

Вывод можно сделать такой — Mathematica обладает обширными возможностями по части выделения элементов списков и представления списков на экране дисплея и в распечатках документов.

Защита от модификации и ее отмена

Как уже отмечалось, объекты Mathematica имеют средства установки и снятия защиты от модификации. Для этого используются следующие функции-директивы:

Protect [s1, s2,...] — устанавливает атрибут защиты от модификации Protected для перечисленных объектов si; Protect ["forml", "form2",...] — устанавливает атрибут защиты от модификации для всех объектов, имена которых сопоставимы с любым из указанных строковых шаблонов formi; Unprotect [s1, s2,...] — удаляет атрибут защиты от модификации Protected для объектов si, что делает возможной их модификацию; Unprotect ["form1", "form2",...] — снимает защиту всех объектов, имена которых текстуально (по буквам) сопоставимы с любым из указанных шаблонов formi.

Приведем наглядный пример модификации встроенной функции логарифма:

Log[7]=2

Set::write : Tag Log in Log[7] is Protected.

2

Итак, здесь предпринята попытка приписать логарифму числа 7 вовсе не свойственное ему значение 2. В ответ система выдала сообщение, что символ Log имеет атрибут Protected, то есть защищен от модификации. С помощью директивы Unprotect снимем защиту:

Unprotect[Log]

{Log}

Теперь выражение Log [ 7 ] можно модифицировать:

Log[7] =2

2

и использовать его уже в новом значении:

Log[7]=2

2

Log[7]+Log[3]

2 + Log[3]

Для отмены произведенной модификации и защиты символа Log от изменений выполните следующие действия:

Log[7]=.

Protect[Log]

{Log}

Теперь можно проверить, что присваивание Log [7] =2 не действует и функция Log работает как положено, возвращая значение In (7) =1. 94591:

Log[7]

Log[7]

N[Log[7]]

1.94591

Защита идентификаторов объектов от модификации является мощным средством контроля правильности вычислений. Эту защиту вряд ли стоит снимать подавляющему большинству пользователей. Тем не менее, возможность устранения защиты позволяет переименовать объект, например, при использовании с ним новых алгоритмов вычислений или при задании системе Mathematica каких-то новых свойств, не присущих ей изначально.

---

---