Что нового мы узнали?
В этом уроке мы научились:
Строить двумерные и трехмерные графики различного вида. Использовать опции графических функций для форматирования графиков. Применять графические директивы. Строить графики по точкам. Использовать графические примитивы. Вставлять в документы графические и иные объекты. Осуществлять синтез звуков.Директивы двумерной графики
Еще одним важным средством настройки графиков являются графические директивы. Синтаксис их подобен синтаксису функций. Однако директивы не возвращают объектов, а лишь влияют на их характеристики. Используются следующие основные директивы двумерной графики:
AbsoluteDashing [ {dl, d2,...}]— задает построение последующих линией пунктиром со смежными (последовательными) сегментами, имеющими абсолютные длины dl, d2, ... (повторяемые циклически). Значения длины di задаются в пикселях; AbsolutePointSize [d] — задает построение последующих точек графика в виде кружков с диаметром d (в пикселях); AbsoluteThickness [d] — задает абсолютное значение толщины (в пикселях) для последующих рисуемых линий; Dashing [{rl, r2,...}] — задает построение последующих линий пунктиром с последовательными сегментами длиной rl, г2, ..., повторяемыми циклически, причем ri задается как доля полной ширины графика; PointSize [d] — задает вывод последующих точек графика в виде кружков с относительным диаметром d, заданным как доля общей ширины графика; Thickness [r] — устанавливает для всех последующих линий толщину г, заданную как доля полной ширины графика.Рисунок 8.7 показывает построение графика функции Бесселя в виде пунктирной линии. Она задается с помощью графической директивы Dashing.

Риc. 8.7. Построение графика функции Бесселя с применением графической директивы Dashing
Применение графических директив совместно с опциями позволяет создавать графики самого различного вида, вполне удовлетворяющие как строгим требованиям, так и различным «извращениям» в их оформлении.
Функция Graphics3D, ее опции и примитивы
Наряду с построением графиков поверхностей, заданных аналитическими выражениями, имеется возможность создания графиков из различных элементарных геометрических объектов, называемых примитивами. Они включаются в список параметров функции Graphics3D [primitives, options] и позволяют строить в пространстве различные простые фигуры. Помимо примитивов двумерной графики могут использоваться примитивы трехмерной графики, приведенные в приложении.
Функция Graphics3D со своими примитивами может использоваться для построения в пространстве различных объектов, например точек, кубиков или многоугольников.
Рисунок 8.36 показывает два варианта размещения случайных точек в пространстве. Для генерации координат точек используется функция Random [ ], возвращающая случайные числа, распределенные по равномерному закону.
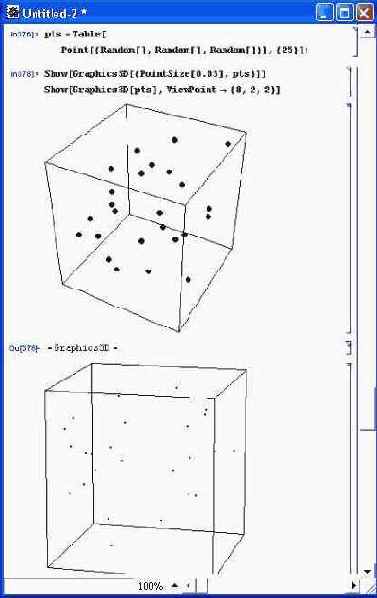
Рис. 8.36. Построение случайных точек в пространстве
Поскольку ограничительный «ящик» не удален, создается впечатление о построении точек внутри куба.
На рис. 8.37 показано построение в пространстве ряда небольших кубиков. Для этого используется примитив Cuboid, повторенный 7 раз. Для воспроизведения набора кубиков, перечисленных в функции GraphicsSD, применяется функция-директива Show.
Нетрудно заметить, что и здесь неплохо работают встроенные алгоритмы удаления невидимых линий. Это дает довольно реалистическое изображение объектов в пространстве.

Рис. 8.37. Построение нескольких кубиков в пространстве
Еще более наглядное представление об этом алгоритме дает рис. 8.38. На нем показано построение в пространстве ряда плоских многоугольников, частично проникающих друг в друга. Нетрудно заметить, что и здесь алгоритм удаления невидимых поверхностей работает превосходно.

Рис. 8.38. Построение взаимно пересекающихся плоских многоугольников в пространстве
Здесь каждый из многоугольников формируется с помощью функции пользователя randpoly [n_], в теле которой используется примитив Polygon. Эта функция формирует случайные многоугольники, выводимые затем функцией-директивой Show.
Построение полиэдров
Язык программирования системы Mathematica позволят создавать средства визуального программирования графических задач. Примером таких средств является приложение Polyhedron Explorer, предназначенное для создания множества объемных фигур класса полиэдров. Это приложение (вместе с системой Mathematica, разумеется) вполне может заменить множество бумажных объемных фигур, которые можно еще встретить в кабинетах математики школ и вузов. Его можно получить по Интернету с файлового сервера фирмы Wolfram Research.
При загрузке этого приложения (как обычного документа) создается панель с окном просмотра фигуры и пультом с множеством кнопок, с помощью которых легко выбрать подходящую фигуру и наблюдать ее в окне просмотра (рис. 8.39).

Рис. 8.39. Работа с приложением PolyhedronExplorer
Обратите внимание на кнопки внизу панели пульта (см. рис. 8.39). Стоит нажать кнопку Paste Code, как фрагмент программы, рисующий выбранную фигуру, будет вставлен в окно редактирования документов — оно видно на рис. 8.39 слева.
Теперь достаточно выполнить этот фрагмент программы, как в строке вывода появится соответствующая фигура. Добавляя те или опции, можно получить нужные изменения ее вида.
В состав примеров системы Mathematica входит немало и других иллюстраций реализации объектно-ориентированного программирования: палитры физических констант и химических элементов (таблица Менделеева), палитры дополнительных функций и т. д. Элементы такого программирования просматриваются и при работе с селектором положения трехмерных графиков (вставка опций с указанием о положении графика).
Графическая функция Plot
Концептуально графики в системе Mathematica являются графическими объектами, которые создаются (возвращаются) соответствующими графическими функциями. Их немного, около десятка, и они охватывают построение практически всех типов математических графиков. Как уже отмечалось, достигается это за счет применения опций и директив.
Поскольку графики являются объектами, то они могут быть значениями переменных. Поэтому Mathematica допускает следующие конструкции:
Plot[Sin[x],{x,0,20}] — построение графика синусоиды; g:=Plot [Sin [x], {х, 0, 20} ] — задание объекта — графика синусоиды — с отложенным выводом; g=Plot [Sin [x], {х, 0, 20} ] — задание объекта — графика синусоиды — с немедленным выводом.Начнем рассмотрение графических возможностей системы с построения простейших графиков функций одной переменной вида у =f(x) или просто f(x). График таких функций строится на плоскости, то есть в двумерном пространстве. При этом используется прямоугольная (декартова) система координат. График представляет собой геометрическое положение точек (х, у) при изменении независимой переменной (абсциссы) в заданных пределах, например от минимального значения xmin до максимального хтах с шагом dx. По умолчанию строятся и линии координатной системы.
Для построения двумерных графиков функций вида f(x) используется встроенная в ядро функция Plot:
Plot [f, {x, xmin, xmax}] — возвращает объект, представляющий собой график функции f аргумента х в интервале от xmin до xmax; Plot[{f1, f2,...}, {x, xmin, xmax}]— возвращает объект в виде графиков ряда функций fi.Функция Plot используется для построения одной или нескольких линий, дающих графическое представление для указанных функций f, f1, f2 и т. д. На рис. 8.1 показано построение графика функции sin(x)/x без использования каких-либо опций (точнее, с набором опций по умолчанию).

Рис. 8.1. Построение двумерного графика
Тут виден как раз тот случай, когда масштаб графика по вертикали выбран системой неудачно — часть графика сверху просто отсекается. В большинстве же случаев применение функции Plot позволяет получить вполне «удобоваримый» график.
Графика и звук
Двумерные и трехмерные графики Опции графических функций Графические директивы Построение графиков лоточкам Получение информации о графических объектах Перестройка и комбинирование графиков Примитивы двумерной и трехмерной графики Импорт графических изображений Вставка объектов Синтез звуков
Графика, как важнейшее средство визуализации вычислений, всегда была козырной картой системы Mathematica и во многом способствовала ее высокой репутации как мирового лидера среди систем компьютерной математики. Обширные графические возможности достигаются при небольшом числе встроенных функций графики за счет их модификации с помощью опций и директив. Благодаря этому Mathematica позволяет строить практически любые виды графиков. Для просмотра и изменения опций графика можно (выделив ячейку с графиком) воспользоваться описанным ранее инспектором опций, в котором есть соответствующий раздел. Однако в этом уроке мы инспектором опций пользоваться не будем — все необходимые опции будут вводиться в соответствующие функции так, как это принято делать при программировании задач графики.
 |
 |
Импорт графических изображений
Несмотря на обширные возможности встроенных в ядро системы Mathematica графических функций, примитивов и опций, они не способны охватить все многообразие графических приложений в математике. Поэтому предусмотрен импорт рисунков, созданных в различных графических системах или в документах самой системы Mathematica.
Описанное выше приложение PolyhedronExplorer позволяет импортировать выбранную фигуру в документ. Для этого достаточно нажать кнопку Paste Graphic. Этот процесс иллюстрирует рис. 8.40.

Рис. 8.40. Пример импорта рисунка из приложения PolyhedronExplorer в документ системы Mathematica
Возможен также импорт изображения с использованием буфера обмена. Нужное -изображение, открытое в каком-либо приложении (например, в графическом редакторе), нужно выделить и поместить в буфер командой Сору или Cut. Затем надо перейти к работе с системой Mathematica. Установив текстовый курсор в нужное место, достаточно исполнить команду меню Edit -> Paste. Если при импорте изображения надо очистить буфер, следует использовать команду Edit -> Paste As -> Paste and Discard.
Импортированное изображение размещается в ячейке вывода, и с ним возможны все манипуляции, характерные для рисунков в ячейках вывода. Так, их можно растягивать или сжимать, а также перемещать в пределах ячейки. Этот способ импорта изображений полезен для создания средствами системы Mathematica электронных книг, уроков и статей.
Вставка графических и иных объектов
Более широкие возможности предоставляет вставка объектов. Как уже отмечалось в уроке 2, она реализуется командой Insert Object из меню Edit. Эта команда открывает окно со списком возможных приложений, которые могут экспортировать объекты в систему Mathematica.
Если, к примеру, выбрать в качестве объекта рисунок графического редактора Paint, то на экране появится окно редактора (рис. 8.41). Теперь в этом редакторе можно создавать любые изображения, например, вроде рожицы, квадрата и эллипса, представленных в окне редактора на рис. 8.41.
Если теперь закрыть окно редактора, то созданный рисунок появится в ячейке вывода документа системы Mathematica (рис. 8.42). Его можно выделять, растягивать в разных направлениях, перемещать и т. д.
Вставка объекта отличается от импорта рисунков (или текстов) одним принципиально важным обстоятельством — объект может редактироваться с автоматическим вызовом приложения, в котором он был создан. Для редактирования объекта, например нашего рисунка, достаточно сделать на нем двойной щелчок. Произойдет загрузка графического редактора, и мы увидим картину, подобную приведенной на рис. 8.41, — в нашем распоряжении будет окно редактора с рисунком, который можно произвольно изменять. После закрытия окна редактора новый рисунок появится в месте вставки.
Разумеется, объектами вставки могут быть не только рисунки, но также тексты и документы других систем. Интересно оценить, насколько Mathematica восприимчива к другим математическим системам. Увы, эта «высокопоставленная мадам» очень критична к своим возможным партнерам или соперницам. Так, она не воспринимает системы Maple V и MATLAB, которые способны соперничать с ней по своим возможностям и скорости работы. Не понимает система и такую «мелочь», как системы начального уровня Derive и MuPAD.
Зато Mathematica сравнительно благосклонно относится к системе Mathcad, известной своим бесподобным интерфейсом и, главное, возможностями задания в документах сложных формул в их вполне естественном виде. Рисунок 8.43 показывает подготовку в Mathcad графика трех функций и вычисление определенного интеграла.

Рис. 8.41. Подготовка объекта в среде графического редактора Paint, вызванного из документа системы Mathematica

Риc. 8.42. Пример вставленного объекта, созданного в среде графического редактора Paint

Рис. 8.43 .Подготовка в Mathcad графика функций и вычисление определенного интеграла
Увы, Mathematica не способна воспринимать документ Mathcad целиком, если в нем больше одного блока, ибо каждый блок воспринимается как отдельный объект.Поэтому приходится располагать блоки Mathcad (поочередно выделяя их) в отдельных ячейках системы Mathematica, что и показано на рис. 8.44.

Рис. 8.44. Документ системы Mathematica с двумя объектами из документа Mathcad
Из этого следует, что Mathematica реализует полноценную объектную связь еще далеко не со всеми программами. И, по всей видимости, это сделано разработчиками намеренно. Не случайно пары «Mathematica — Word» и «Mathematica — Excel» поставляются фирмой Wolfram как самостоятельные программные продукты.
Опции функции Plot
По мере усложнения задач, решаемых пользователем, его рано или поздно перестанут устраивать графики, получаемые при автоматическом выборе их стиля и иных параметров. Для точной настройки графиков Mathematica использует специальные опции графических функций Для вывода их списка надо использовать команду Options [Plot]. Полный список опций дан в приложении.
Опции внутри.графических функций задаются своим именем name и значением value в виде
name -> value
Наиболее распространённые символьные значения опций:
Automatic — используется автоматический выбор; None — опция не используется; All — используется в любом случае; True — используется; False — не используется.Многие опции могут иметь числовые значения. В сомнительных случаях рекомендуется уточнять форму записи опций и их значений по оперативной справочной смстеме. Рассмотрим примеры применения опций двумерной графики.
Мы уже отметили неудачный выбор масштаба в случае, представленном на рис. 8.1. Очевидно, этот недостаток графика легко исправить, введя коррекцию масштаба по оси у. Это и сделано в примере, показанном на рис. 8.2. Для изменения масштаба использована опция PlotRange->{ -.25,1.2}. Нетрудно догадаться, что эта опция задает пределы отображения графика по вертикали от -0.25 до 1.2.

Рис. 8.2. График функции sin(x)/x с масштабом, дающим его отображение в полном виде
По умолчанию система строит графики, не указывая надписей ни по осям координат (кроме букв х и г/), ни в верхней части графика. Такая надпись на графике по центру сверху называется титульной. Рисунок 8.3 показывает построение графика с надписями у координатных осей. Для создания таких надписей используется опция Axes Label. После нее указывается список, содержащий две надписи — одну для оси х, вторую — для оси у. Надписи указываются в кавычках. Таким образом, задание опции выглядит следующим образом: AxesLabel-> {"X value","f(x)}.

Рис. 8.3. График с надписями по координатным осям
С помощью опции Axes со значением None можно убрать с графика отображение осей.
Вид получающегося при этом графика показан на рис. 8.4. При его построении, кроме удаления осей, использована опция PlotLabel для вывода указанной в качестве ее значения титульной надписи.

Рис. 8.4. График без координатных осей, но с титульной надписью
Часто возникает необходимость построения на одном рисунке нескольких графиков одной и той же функции, но при разных значениях какого-либо параметра — например, порядка специальных математических функций. В этом случае они могут быть заданы в табличной форме. Рисунок 8.5 дает пример построения пяти графиков функций Бесссля.
Рисунок 8.5 иллюстрирует недостаток одновременного представления нескольких графиков, создаваемого по умолчанию, — все графики построены одинаковыми линиями, и не сразу ясно, какой график к какой функции относится. Рисунок 8.6 показывает возможности управления стилем линий (густотой черного цвета) графиков с помощью опции PlotStyle. Если желательно выделение линий разными цветами, удобно использовать в качестве значения опции PlotStyle список вида {Hue [cl] , Hue [с2] ,...}, где параметры c1, с2, ... выбираются от 0 до 1 и задают цвет соответствующей кривой.
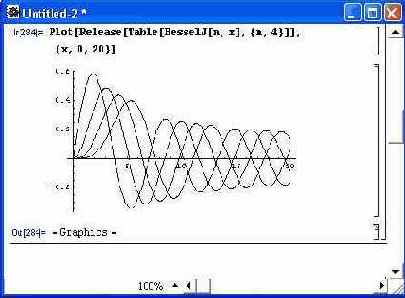
Рис. 8.5. Семейство функций Бесселя на одном графике

Риc. 8.6. Построение графиков линиями разного стиля
Применение других опций позволяет задавать массу свойств графиков, например цвет линий и фона, вывод различных надписей и т. д. Помимо представленных примеров, полезно просмотреть и множество примеров построения двумерных графиков, приведенных в справочной системе Mathematica.
Перестроение и комбинирование графиков
При построении графиков часто требуется изменение их вида и тех или иных параметров и опций. Этого можно достичь повторением вычислений, но при этом скорость работы с системой заметно снижается. Для ее повышения удобно использовать специальные функции перестроения и вывода графиков, учитывающие, что узловые точки уже рассчитаны и большая часть опций уже задана. В этом случае удобно использовать следующую функцию-директиву:
Show [plot] — построение графика; Show [plot, option -> value] — построение графика с заданной опцией; Show[plotl, plot2,...] — построение нескольких графиков с наложением их друг на друга.Директива Show полезна также и в том случае, когда желательно, не трогая исходные графики, просмотреть их при иных параметрах. Соответствующие опции, меняющие параметры графиков, можно включить в состав директивы Show. Другое полезное применение директивы — объединение на одном графике нескольких графиков различных функций или объединение экспериментальных точек и графика теоретической зависимости. Для этого также удобна функция Display-Together, которая будет описана при описании пакета расширения Graphics в уроке 14. В отличие от функции Show, она позволяет объединять графики без предварительного построения каждого из них.
Рисунок 8.9 показывает создание двух графических объектов g1 и g2 с отложенным выводом, а затем построение графиков функций и применение директивы Show для создания объединенного графика. В этом случае директива Show вначале строит исходные графики отдельно, а затем создает объединенный график. В приведенных ниже примерах оставлен только объединенный график, другие удалены командой меню Edit > Clear.

Рис. 8.9. Построение двух графических объектов и их объединение
Разумеется, при использовании директивы Show надо побеспокоиться о выравнивании масштабов графиков, налагаемых друг на друга. Полезно особо обратить внимание на возможность присваивания графиков функций переменным (в нашем примере — g1 и g2) в качестве значений. Такие переменные становятся графическими объектами, используемыми директивой Show для вывода на экран дисплея.
Директива Show часто применяется, когда надо построить на одном графике кривую некоторой функции и представляющие ее узловые точки (например, при построении кривых регрессии в облаке точек исходных данных).
Построение графика по точкам — функция List Plot
Часто возникает необходимость построения графика по точкам. Это обеспечивает встроенная в ядро графическая функция ListPlot:
ListPlot [ {yl, у2,...}]— выводит график списка величин. Координаты х принимают значения 1, 2, ...; ListPlot [{{x1, y1}, {х2, у2 },...}]—выводит график списка величин с указанными х- иy-координатами.В простейшем случае (рис. 8.8) эта функция сама задает значения координаты х= 0, 1, 2, 3, ... и строит на графике точки с координатами (х, у), выбирая у последовательно из списка координат.

Рис. 8.8. Построение графика по точкам
Можно заметить характерный недостаток построений — точки (особенно при небольшом размере) имеют вид, заметно отличающийся от идеального круга. Функция ListPlot, особенно в ее второй форме (с заданными координатами х и г/), удобна для вывода на график экспериментальных точек.
Получение информации о графических объектах
Порой некоторые детали построения графиков оказываются для пользователя неожиданными и не вполне понятными. Причина этого кроется во множестве опций, которые могут использоваться в графиках, причем в самых различных сочетаниях. Поэтому полезно знать, как можно получить информацию о свойствах графических объектов. Порой небольшая модификация опций (например, замена цвета линий или фона) делает график полностью удовлетворяющим требованиям пользователя. Информацию об опциях графического объекта g дают следующие функции:
FullAxes [g] — возвращает список опций координатных осей; Options [g] — возвращает упрощенный список опций; FullOptions [g] — возвращает полный список опций; InputForm[g] — возвращает информацию о графике (включая таблицу точек).Пусть задан графический объект g: g:=Plot[Sin[x],{х,-10,10}]
Ниже представлено получение упрощенного списка опций этого графического объекта:
Options[g]
{PlotRange -> Automatic, AspectRatio ->1/GoldenRatio,
DisplayFunction :> $DisplayFunction, ColorOutput -> Automatic, Axes -> Automatic, AxesOrigin -> Automatic, PlotLabel -> None, AxesLabel -> None, Ticks -> Automatic, GridLines -> None, Prolog -> {}, Epilog -> {}, AxesStyle -> Automatic, Background -> Automatic, DefaultColor -> Automatic, DefaultFont :> $DefaultFont, RotateLabel -> True, Frame -> False, FrameStyle -> Automatic, FrameTicks -> Automatic!, FrameLabel -> None, PlotRegion -> Automatic, ImageSize -> Automatic, TextStyle :> $TextStyle, FormatType :> $FormatType}
Для получения полного списка опций вместе с их значениями можно использовать функцию FullOptions. Аналогично можно получить и иные данные — они не приводятся ввиду громоздкости выводимой информации. Анализ графиков с применением этих функций может оказаться весьма полезным при построении и редактировании сложных графиков.
Функции FullOptions и Options можно также использовать в следующем виде:
Options [g, option] — возвращает значение указанной опции option; FullOptions [g, option] — возвращает значение указанной опции option.В этом случае можно получить информацию по отдельной опции.
Построение графиков плотности
Функцией двух переменных f(x, у) может описываться плотность некоторой среды. Для построения графиков плотности используются следующие графические функции:
DensityGraphics [array] — является представлением графика плотности; DensityPlot[f, {х, xmin, xmax}, {у, ymin, ymax}] — строит график плотности f как функции от х и у; ListDensityPlot [array] — формирует график плотности из массива величин высот.С этими функциями используется множество (в основном уже рассмотренных) опций. Их перечень можно получить с помощью функции Options.
Внешне график плотности похож на контурный график. Однако для него характерно выделение элементарных участков (с равной плотностью) в форме квадратиков (рис. 8.18).

Рис. 8.18. График плотности
График плотности (рис. 8.18) также дан в режиме PostScript. Цветная функциональная раскраска таких графиков тоже возможна (см. опции, указанные выше для контурных графиков).
Построение графиков поверхностей — функция Plot 3D
Функция двух переменных z = f(x, у) образует в пространстве некоторую трехмерную поверхность или фигуру. Для их построения приходится использовать координатную систему с тремя осями координат: х, у и z. Поскольку экран дисплея плоский, то на самом деле объемность фигур лишь имитируется — используется хорошо известный способ наглядного представления трехмерных фигур с помощью аксонометрической проекции.
Вместо построения всех точек фигуры обычно строится ее каркасная модель, содержащая линии разреза фигуры по взаимно перпендикулярным плоскостям. В результате фигура представляется в виде совокупности множества криволинейных четырехугольников. Для придания фигуре большей естественности используются алгоритм удаления невидимых линий каркаса и функциональная закраска четырехугольников с целью имитации бокового освещения фигуры.
Для построения графиков трехмерных поверхностей используется основная графическая функция Plot 3D:
Plot3D[f, {x, xmin, xmax), {у, ymin, ymax}] — строит трехмерный график функции f переменных х и у; Plot3D[{f, s}, {x, xmin, xmax}, {y, ymin, ymax}] — строит трехмерный график, в котором высоту поверхности определяет параметр f, а затенение — параметр s.
На рис. 8.19 показан пример построения поверхности, описываемой функцией двух переменных cos(x у) при х и у, меняющихся от -3 до 3.
Поверхность строится в виде каркаса с прямоугольными ячейками с использованием функциональной окраски. Все опции заданы по умолчанию.

Рис. 8.19. Пример построения поверхности cos(xy) функцией Plot3D с опциями по умолчанию
Этот график будем считать исходным для демонстрации его модификаций, получаемых путем изменения опций.
Опции и директивы трехмерной графики
Для модификации трехмерных графиков могут использоваться многочисленные опции и директивы, список которых дан в приложении. Их применение позволяет строить большое число графиков различных типов даже при задании одной и той же поверхности. В качестве примера рассмотрим отдельные кадры документа, демонстрирующего влияние опций на вид трехмерной математической поверхности.
На рис. 8.20 показана исходная поверхность (см. рис. 8.19), построенная с применением опции PlotPoint->50. Это означает, что поверхность по каждой оси делится на 50 частей (в исходном графике по умолчанию используется деление на 10 частей). Масштаб по вертикали задается автоматически, с тем чтобы все высоты поверхности не ограничивались.
На рис. 8.21 показана та же поверхность, полученная с применением опции PlotRange-> {0, 0.5}, срезающей верхнюю часть поверхности (точки с ординатами выше 0.5). График поверхности при этом существенно меняется (сравните с рис. 8.20).

Рис. 8.20. Поверхность рис. 8.19 с большим числом ячеек

Рис. 8.21. Математическая поверхность с отсеченной верхней частью
Опция Boxed -> False удаляет ограничивающие рамки, образующие «ящик», в который вписывается построенная трехмерная поверхность (рис. 8.22). Остаются лишь координатные оси.
Опция Viewpoint позволяет включить при построении отображение перспективы и изменять углы, под которыми рассматривается фигура. Рисунок 8.23 иллюстрирует применение этой опции.

Рис. 8.22. Построение трехмерной поверхности без ограничительного «ящика»

Рис. 8.23. Математическая поверхность, построенная с учетом перспективы
Опция Mesh -> False позволяет удалить линии каркаса фигуры. Нередко это придает фигуре более естественный вид (рис. 8.24) — обычно мы наблюдаем такие фигуры без линий каркаса.
В ряде случаев, напротив, именно линии каркаса несут важную информацию. Система строит каркас трехмерных поверхностей двумя способами — с использованием и без использования алгоритма удаления невидимых линий. Рисунок 8.25 показывает результат построения при использовании алгоритма удаления невидимых линий. Нетрудно заметить, что в этом случае поверхность выглядит достаточно эстетично даже без применения функциональной закраски.

Рис. 8.24. Математическая поверхность с удаленными линиями каркаса

Рис. 8.25. Построение каркаса математической поверхности с использованием алгоритма удаления невидимых линий
На рис. 8.26 показано построение каркаса без удаления невидимых линий. Такой вид математическая поверхность имеет, если представить ее построенной из тонких проволочек, висящих в пространстве. Это дает дополнительную информацию о пространственной фигуре, но эстетически она выглядит хуже, чем фигура, построенная с применением алгоритма удаления невидимых линий каркаса.
Таким образом, как и ранее, применение опций позволяет легко управлять характером и типом графиков, придавая им вид, удобный для заданного применения. На рис. 8.27 показан пример построения трехмерного графика с применением одновременно нескольких опций.

Риc. 8.26. Построение каркаса математической поверхности без использования алгоритма удаления невидимых линий

Риc. 8.27. Пример построения трехмерного графика с несколькими опциями
Приведенные примеры самым наглядным образом показывают, насколько легко модифицируются графики с помощью различных опций. Разумеется, есть множество возможностей для иных модификаций, которые пользователь может опробовать самостоятельно.
В разделе приложения, посвященном данному уроку, указан ряд дополнительных директив и опций трехмерной графики. С их помощью можно расширить возможности построения графиков.
Читателю рекомендуется самостоятельно построить графики ряда поверхностей с использованием различных опций.
Графическая функция ListPlot3D
Часто трехмерная поверхность задается массивом своих высот (аппликат). Для построения графика в этом случае используется графическая функция ListPlotSD:
ListPlot3D [array] — строит трехмерный график поверхности, представленной массивом значений высот; ListPlot3D [array, shades] — строит график так, что каждый элемент поверхности штрихуется (затеняется) согласно спецификации shades. Plot Joined — дополнительная опция для ListPlot, указывающая, следует ли соединять линией точки, нанесенные на график.
Пример применения функции ListPlotSD показан на рис. 8.28. График построен по данным таблицы tS, формирующей значения аппликат поверхности, которая описывается функцией cos(xy).

Рис. 8.28. Пример применения функции ListPlotSD
Командой Options [ListPlot3D] можно вывести полный список опций данной функции, чтобы использовать их для модификации графиков, которые строит эта функция.
 |
 |
 |
Построение контурных графиков
Контурные графики, или графики линий равных высот, используются для отображения поверхностей на плоскости. Они удобны для выявления всех экстремумов функций в пределах области графика. Такие графики являются линиями пересечения поверхности с секущими горизонтальными плоскостями, расположенными параллельно друг под другом. Они часто используются в картографии.
Основными функциями и директивами для построения контурных графиков являются следующие:
ContourPlot[f,{x, xmin, xmax}, {у, ymin, ymax}] — порождает контурный график f как функции от х и у; ContourGraphics [array] — представляет контурный график массива array; ListContourPlot[array] — формирует контурный график из массива величин высот.Этих функций достаточно для построения практически любых монохромных графиков такого типа.
Для управления возможностями графической функции ContourPlot используются опции, полный список которых выводит команда Options [ContourGraphics ]. Помимо уже рассмотренных ранее опций используются следующие:
ColorFunction — задает окраску областей между линиями; Contours — задает число контурных линий; ContourLines — задает прорисовку явных (explicit) контурных линий; ContourShading — задает затенение областей между контурными линиями; ContourSmoothing — задает сглаживание контурных линий; ContourStyle — задает стиль рисуемых линий для контурных графиков; MeshRange — задает области изменения х- и y-координат.Рисунок 8.15 показывает построение контурного графика с окраской промежуточных областей между линиями. Окраска обеспечивается опцией ColorFunction-> Hue. Опция ContourSmoothing -> True задает сглаживание контурных линий.

Рис. 8.15. Контурный график поверхности sin(x у) с закраской областей между линиями равного уровня оттенками серого цвета
Следующий пример (рис. 8.16) иллюстрирует эффективность применения опции ContourShading. Если задать ее значение равным False, то заполнение пространства между линиями будет отсутствовать. Таким образом, в данном случае строятся только линии равного уровня.

Рис. 8.16. Контурный график, представленный только линиями равного уровня
Иногда график оказывается более наглядным, если убрать построение контурных линий, но оставить закраску областей между линиями. Такой вариант графика более предпочтителен, если нужно наблюдать качественную картину. Для построения такого графика надо использовать опцию ContourLine->False (рис. 8.17).

Рис. 8.17. Контурный график без пиний равного уровня
В данном случае используется вариант монохромной окраски областей между линиями (PostScript). Он может оказаться предпочтителен, например, если предполагается печать графика монохромным принтером.
Примитивы двумерной графики
Примитивами двумерной графики называют дополнительные указания, вводимые в функцию Graphics [primitives, options], которая позволяет выводить различные примитивные фигуры без задания математических выражений, описывающих эти фигуры. Примитивы могут выполнять и иные действия. Они заметно увеличивают число типов графиков, которые способна строить система Mathematica. Имеются примитивы для построения окружностей, эллипсов, кругов, овалов, линий и полигонов, прямоугольников и текстов. Полное описание примитивов дано в разделе приложения, посвященном данному уроку. Примитивы задаются подобно графическим функциям, например, Circle[{x, у}, r] строит окружность с радиусом г и центром в точке {х, у}.
Рисунок 8.10 показывает применение функции Graphics для построения одновременно трех графических объектов: отрезка прямой, заданного координатами его концевых точек, окружности с центром (0, 0) и радиусом 0.8 и текстовой надписи «Привет!». Каждый объект задан своим примитивом. Из-за искажения масштаба дисплеем компьютера окружность выглядит как эллипс.

Рис. 8.10. Построение трех графических объектов с помощью примитивов двумерной графики
На другом рисунке (рис. 8.11) представлено построение пятиугольника, заданного координатами его вершин.
Приведенные примеры поясняют технику применения графических примитивов. Но они, разумеется, не исчерпывают всех возможностей этого метода построения геометрических фигур и объектов. Все указанные примитивы используются при построении как двумерных, так и трехмерных графиков.

Рис. 8.11. Построение пятиугольника
Графики функций, заданных в параметрической форме
Построение графиков в полярной системе координат возможно двумя способами. Первый способ основан на использовании обычной декартовой системы координат. Координаты каждой точки при этом задаются в параметрическом виде: x = f
x
(t) и у
=
f
y
(t), где независимая переменная t меняется от минимального значения £
min
до максимального t
mах
с шагом dt.
Особенно удобно применение таких функций для построения замкнутых линий, таких как окружности, эллипсы, циклоиды и т. д. Например, окружность радиусом R может быть задана в следующей параметрической форме: х = R cos(t) и у = R sin(t), если t меняется от 0 до 2п. В общем случае радиус также может быть функцией параметра t.
Для построения параметрически заданных функций используются следующие графические средства:
ParametricPlot [ {fx, fy}, {t, tmin, tmax} ]—строит параметрический график с координатами f х и f у (соответствующими х и у), получаемыми как функции от t;
ParametricPlot [{{fx, fy}, {gx, gy},...}, {t, tmin, tmax}] —строит графики нескольких параметрических кривых.
Функции f x, f у и т. д. могут быть как непосредственно вписаны в список параметров, так и определены как функции пользователя.
Рисунок 8.12 показывает построение параметрически заданной фигуры Лиссажу. Она задается функциями синуса и косинуса с постоянным параметром R и аргументами, кратными t. Эти фигуры наблюдаются на экране электронного осциллографа, когда на его входы X и Y подаются синусоидальные сигналы с кратными частотами.

Рис. 8.12. Построение фигуры Лиссажу
На одном графике можно строить две и более фигур с заданными параметрически уравнениями. На рис. 8.13 показан пример такого построения — строятся две фигуры Лиссажу, причем одна из них является окружностью. Больше двух фигур строить нерационально, так как на черно-белом графике их трудно различить.
Теперь рассмотрим второй способ построения графиков в полярной системе координат (рис. 8.14). Здесь каждая точка является концом радиус-вектора R(t), причем угол t меняется от 0 до 2я. На рис. 8.14 функция R(t) задана как функция пользователя R[t_] с использованием образца t_ для задания локальной переменной t в теле функции.
Изменение параметра R позволяет заметно увеличить число отображаемых функций — фактически, их бесконечно много. Помимо описанной фигуры на рис. 8.14 дополнительно построена линия окружности единичного радиуса.
Чтобы она имела правильные пропорции на экране, задана опция AspectRatio->l.

Рис. 8.13. Построение на одном графике двух фигур Лиссажу

Рис. 8.14. Построение графика функции в полярной системе координат
 |
 |
 |
Синтез звуков
Mathematica, в отличие от других систем компьютерной математики, имеет средства для синтеза звука. Сопровождение звуком описания некоторых математических закономерностей (например, биений, развития взрывных процессов и т. д.) делает это описание более понятным и естественным. Особенно удобна эта возможность в теоретической акустике и в технике аналоговой и цифровой обработки акустических сигналов. Таким образом, при более серьезном рассмотрении можно найти немало прикладных задач, где звуковое сопровождение их решения полезно и является важной составляющей общего описания результатов решения.
Возможности синтеза звука становятся доступными, если компьютер оборудован звуковой картой класса Sound Blaster фирмы Creative Labs или совместимой с ней. К карте должна быть подключена стереофоническая акустическая система для воспроизведения звуков. Возможен синтез как монофонических, так и стереофонических звуков.
С синтезируемым звуком связан некоторый графический образ — ячейка. Этот графический образ имеет вид осциллограмм звуковых сигналов по обоим стереоканалам. Если такая ячейка выделена, то возможен запуск воспроизведения звука с помощью главного меню, как описывалось в уроке 2.
Для синтеза звуков в системе Mathematica используются следующие функции:
ListPlay [ {a1l, a2,...}] — проигрывает звук с амплитудой, заданной последовательностью уровней ai; Play[f, {t, tmin, tmax}] — воспроизводит звук с амплитудой, заданной f как функцией от времени t в секундах между значениями tmin и tmax; PlayRange — опция для Play и родственных функций, указывающая, какой диапазон уровней звуковых амплитуд должен использоваться; SampleDepth — опция для звуковых примитивов, устанавливающая количество бит для кодирования уровней амплитуды звуковых сигналов; SampledSoundFunction [f, n, r] — звуковой примитив; воспроизводит звук с частотой дискретизации г герц; значения дискретных отсчетов генерируются применением функции f к последовательным целым от 1 до л; SampledSoundList [ {al, а2,...},r] — звуковой примитив, воспроизводящий звук, амплитуда которого имеет уровни ai с дискретностью г раз в секунду; SampleRate — опция для звуковых примитивов, устанавливающая частоту дискретизации звука в герцах; Sound [primitives] — представляет звук; $SoundDisplayFunction — возвращает значение по умолчанию для опции Display Function в звуковых функциях.
Некоторые из указанных функций напоминают графические функции, и это не случайно.
Идеология применения этих функций та же, что при использовании функций графики. Звуковые объекты имеют много схожего с графическими объектами, их можно наряду с последними включать в различные функции-директивы. Таким образом, единство работы со звуком и графикой обеспечено специально.
Рисунок 8.45 показывает использование функции Sound для создания звукового объекта. Графически этот объект представляет собой сдвоенную «осциллограмму» звука. Слово «осциллограмма» не случайно взято в кавычки — на самом деле речь идет лишь о некотором графическом представлении звуковых сигналов, отдаленно напоминающем осциллограмму. К тому же вид этого отображения сильно зависит от компьютерной платформы, на которой установлена система Mathe-matica и даже от применяемых в компьютере видеосредств.

Рис. 8.45. Создание звукового объекта
Принятый в системе способ синтеза звуков имеет определенные недостатки. Звуковые средства слишком привязаны к математике — для задания звука надо описать звуковые колебания математической формулой. Наконец, надо отметить, что графическая интерпретация звукового объекта не всегда понятна — например, неясно, что нового дает нижняя осциллограмма при синтезе монофонического звука.
Специальные средства визуализации и звука
Системы Mathematica содержат множество средств, повышающих наглядность представления (визуализации) результатов вычислений — как простых, так и сложных. К ним можно отнести особые виды трехмерной графики, используемые при параметрическом задании поверхностей, в том числе пересекающихся в пространстве, а также графики объемных фигур — полиэдров. Возможности визуализации расширяются при использовании импортируемых рисунков и вставки графических объектов. К специфическим приемам визуализации относится и применение звуковых объектов, способных генерировать и воспроизводить звуки при наличии в компьютере звуковой карты.
Параметрическая трехмерная графика
Особый шик построениям трехмерных фигур и поверхностей придает функция ParametricPlot3D, в которой предусмотрено параметрическое задание всех трех функций, описывающих координаты точек. Каждая из функций, задающих координаты точек, является функцией двух переменных.
Функция ParametricPlot3D используется в следующих видах:
PararnetricPlot3D[ {fx, fy, fz}, {t, tmin, tmax}, {u, umin, umax} ] — строит трехмерную поверхность, параметризованную по t и u; ParametricPlot3D[{fx, fy, fz}, {t, tmin, tmax}] — создает трехмерную пространственную кривую, параметризованную переменной t, которая изменяется от tmin до tmax; ParametricPlot3D[ { fx, fy, fz, s},...] — выполняет затенение графика в соответствии с цветовой спецификацией s; ParametricPlot3D[ { {fx, fy, fz}, {gx, gy, gz},...},...] — строит несколько объектов вместе.Эта функция имеет множество опций, которые можно вывести с помощью команды Options [ParametricPlotSD]. Большая часть из них уже рассматривалась ранее. При этом даже при использовании только опций, заданных по умолчанию, можно получить любопытные построения. На рис. 8.29 показан простой пример применения функции ParametricPlot3D для построения замкнутой линии, расположенной в пространстве. Это, так сказать, объемный вариант, фигур Лиссажу, построение которых было описано ранее.
Параметрическое задание функций позволяет легко строить сложные пространственные фигуры, визуально весьма напоминающие реальные объекты.
Покажем это на трех характерных примерах.

Рис. 8.29. Построение пространственной кривой, заданной в параметрической форме
Первым примером может служить фигура «рог изобилия», показанная на рис. 8.30. По существу, это раскручивающаяся объемная спираль, диаметр которой постепенно нарастает.

Рис. 8.30. Построение фигуры «рог»
Другой пример — объемное кольцо с сечением, напоминающим знак бесконечности (бесконечность). Результат построения показан на рис. 8.31. Обратите внимание на интересный эффект — из кольца удален сектор, что позволяет рассмотреть его внутреннее строение. Все, что потребовалось для создания этого эффекта, — это задать верхний предел изменения переменной t равным 2л - 0.6. Если сделать этот предел равным 2л, то кольцо станет непрерывным.

Рис. 8.31. Построение кольца с удаленным сектором

Рис. 8.32. Построение сферы с удаленным сегментом
Третий пример такого рода — построение объемной сферы. Этот пример показан на рис. 8.32. Здесь также использован прием изменения значений переменной t для получения выреза сегмента сферы. Опять-таки, задав изменение t от 0 до 2л, можно получить построение всей сферы без выреза.
Любопытно отметить, что описанные приемы создания вырезов в объемных фигурах позволяют наблюдать внутреннюю часть фигур, которая обычно (без вырезов) не видна. Это делает описанный прием построения фигур с вырезом достаточно продуктивным.
Построение фигур, пересекающихся в пространстве
Пожалуй, наиболее впечатляющими являются построения трехмерных фигур, пересекающихся в пространстве. Для этого достаточно представить каждую фигуру в виде графического объекта, а затем с помощью директивы Show вывести их на одном графике. При этом Mathematica автоматически рассчитывает линии пересечения фигур и строит график так, чтобы заслоненные ячейки фигур не были видны.
Проиллюстрируем это на примере. На рис. 8.33 показано задание и построение одного графического объекта gl — объемной спирали, полученной сворачиванием ленты.

Рис. 8.33. Построение объекта gl — объемной спирали
Второй объект, построение которого представлено на рис. 8.34, — это объемное кольцо. Его построение было описано выше. В конце части документа, показанного на рис. 8.34, задана функция Show для вывода объектов на одном графике.

Рис. 8.34. Построение объекта g2 — объемного кольца с удаленным сегментом
Рисунок 8.35 демонстрирует комбинированный график, построенный функцией Show. Он показывает кольцо, через отверстие которого проходит объемная спираль. Вырез в кольце показывает, как спираль проходит внутри кольца.

Рис. 8.35. Построение комбинированного объекта — спираль проходит внутри кольца
Графики такого типа дают большие возможности визуализации трехмерных поверхностей и фигур.
Трехмерная графика
Трехмерная графика, называемая также ЗD-графикой, представляет в аксонометрической проекции объемное изображение поверхностей или фигур, которые описываются либо функциями двух переменных, либо параметрически заданными координатами объектов. В данном разделе описаны многие способы построения трехмерных графиков, начиная от простых контурных графиков и кончая графиками поверхностей и фигур с функциональной окраской.