Установка аргумента цвета — ArgColor
При построении графиков в полярной системе координат полезно использовать цвет, зависящий от фазы комплексного числа. Для этого в подпакете ArgColor служат следующие функции:
ArgColor [z] — дает цвет, определяемый фазой комплексного аргумента z; ArgShade [ z ] — дает уровень серого цвета, определяемый фазой комплексного аргумента z.

Рис. 14.8. Построение кругов, расположенных по окружности, с разной степенью окраски серыми полутонами
Действие функции ArgShade иллюстрирует показанный на рис. 14.8 пример. Он строит 12 расположенных по окружности кругов с разной степенью окраски (от белого до черного) с помощью функции ArgShade. Заменив в этом программном модуле функцию ArgShade на ArgColor, вы сможете наблюдать окраску кругов разными цветами.Установка цветовой системы — Colors
Обычно цвета задаются в цветовой системе RGB (Red-Green-Blue). В подпакете Colors содержатся функции установки цвета, заданного в других известных цветовых системах: CMYColor [с, m, у] — установка цвета по системе CMY (Cyan-Magenta-Yellow); YIQColor[y,i,q] — установка цвета по системе YIQ (используется в телевизионном стандарте NTSC); HLSColor [h, I, s ] — установка цвета по системе HLS (Hue-Lightness-Saturation); AllColors — переменная-функция, выводящая список установленных цветов. Примеры применения функций даны ниже:<<Graphics" Colors" RGBColor[0.5, -O.I, 0.2] RGBColor[0.53, 0.4, 0.957] RGBColor[0.5, -0.1, 0.2] RGBColor[0.53, 0.4, 0.957] Orange RGBColor[l., 0.5, 0.]Кроме этого в подпакете имеется внушительная таблица англоязычных наименований разных цветов и цветовых оттенков — она выводится функцией AllColors. Их можно использовать для задания в качестве аргумента у функций, управляющих цветами. Например, шоколадный цвет можно задать следующим образом:
Chocolate RGBColor[0.823496, 0.411802, 0.117603]Подпакет Arrow служит для построения стрелок на двумерных графиках (или самих по себе). Для этого предназначена функция Arrow [start, finish, opts], которая строит стрелку по координатам ее начала start и конца finish. Рекомендуется просмотреть список опций этой функции. Рисунок 14.9 показывает построение множества стрелок, острия которых находятся на спирали. Для этого координаты стрелок задаются в параметрическом виде.
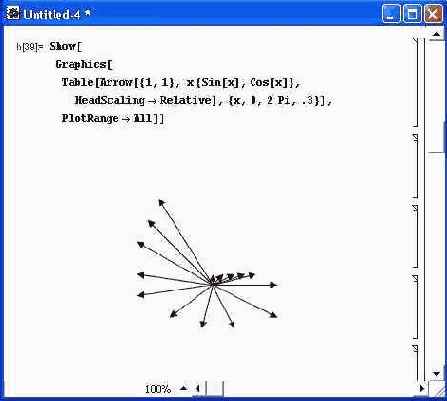
Рис. 14.9. Построение множества стрелок с остриями, расположенными по спирали
Другой пример, представленный на рис. 14.10, иллюстрирует построение двуна-равленной стрелки, опирающейся на иглу, стоящую на кресте, — получается своеобразная модель компаса.

Рис. 14.10. Построение двунаправленной стрелки, опирающейся на иглу
Построение стрелок оживляет многие типы графиков. Их можно использовать, к примеру, для указания особых точек на графиках.Графики комплексных функций — ComplexMap
Подпакет ComplexMap задает функции для построения графиков комплексных функций комплексной переменной путем демонстрации преобразования координатных линий: CartesianMap [f, {xmin,xmax}, {ymin,ymax}] — строит изображение декартовых координатных линий после их преобразования функцией f; PolarMap[f, {rmin,rmax}, {thetamin, thetamax} ] — строит изображение координатных линий полярной системы после их преобразования функцией f. Действие этих довольно простых функций иллюстрирует рис. 14.11.
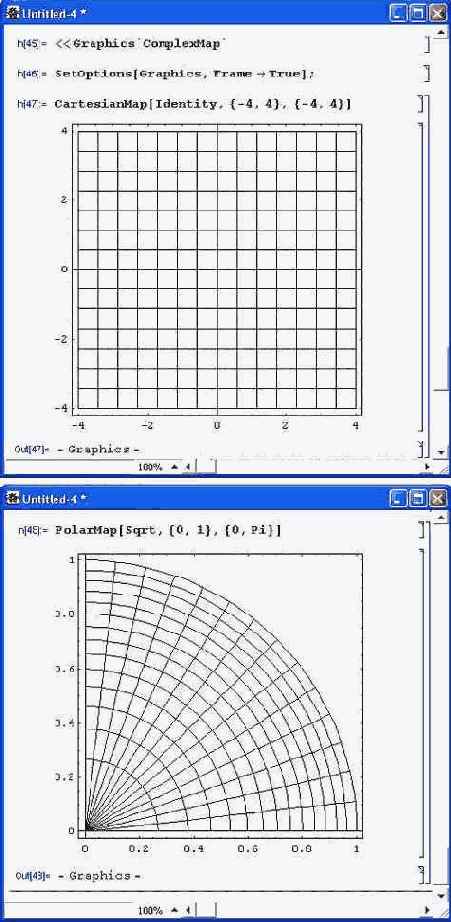
Рис. 14.11. Построение неискаженной декартовой координатной сетки (сверху) и полярной координатной сетки, искаженной воздействием функции Sqrt (снизу)
Построение объемных контурных графиков — ContourPlot3D
В подпакете ContourPlotSD заданы две функции, которые строят контурные объемные графики. Напоминаем, что функции ядра ContourPlot и ListContourPlot строят только двумерные графики этого типа. Для построения объемных контурных графиков надо использовать следующие функции:
ContourPlotSD[f,{x,xmin,xmax},{у,ymin,углах),{z,zmin,zmax)] — строит трехмерный контурный график функции f трех переменных: х, у и z; ListContourPlot3D[f, { fill, f 112,...}, { f 121, f 122,...},...},...}] -строит контурный график по данным трехмерного массива значений f . На рис. 14.12 показано построение сферы с отверстием с помощью первой из этих функций. Обратите внимание на то, что никаких усилий по созданию в сфере отверстия не требуется, Оно получено просто усечением ограничительного «ящика», в котором размещается сфера. Для этого пределы по оси у заданы как {-1.2,2}, тогда как по остальным осям используются пределы {-2,2}.
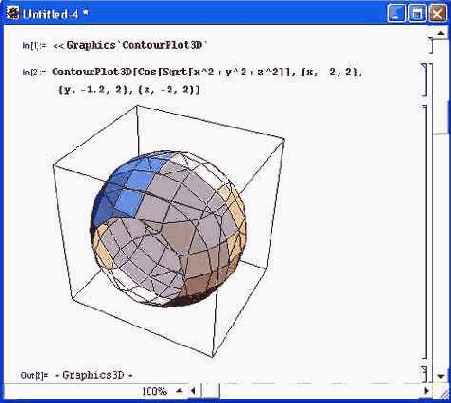
Рис. 14.12. Построение сферы с отверстием
Интересные возможности открывает опция Contours, которая позволяет как бы раздвинуть в пространстве части трехмерной поверхности. Рисунок 14.13 демонстрирует ее действие.
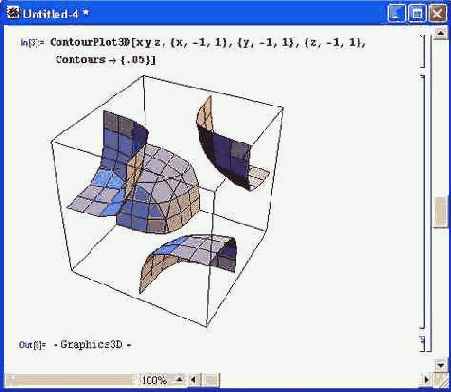
Риc. 14.13. Построение частей сферы в пространстве
Вторая функция— ListContourPlot3D — позволяет строить ряд фигур или поверхностей в пространстве. Пример такого построения дан на рис. 14.14. Масштабы осей подобраны так, чтобы фигура была несколько обрезана справа, что создает изображение отверстия во внутренней яйцеобразной фигуре.

Рис. 14.14. Построение яйцо, вложенного в параболы
Как видно из этих примеров, применение описанных функций позволяет упростить построение трехмерных поверхностей и добиться интересных эффектов.Построение графиков с окраской внутренних областей — FilledPlot
Многие графики сильно выигрывают при их построении с закраской. Например, чтобы проиллюстрировать значение определенного интеграла от какой-то функции f(x), достаточно просто закрасить ее график в диапазоне изменения х от нижнего предела интегрирования а до верхнего b. Для построения подобных графиков в подпакете FilledPlot имеется ряд полезных функций. Начнем их описание с основных: FilledPlot [f, {х, xmin, xmax} ] — строит график функции/(x) с окраской площадей, образованных линией функции и горизонтальной осью х. По умолчанию действуют опции Fills->Automatic и Curves->Back (то есть кривые строятся на заднем плане, при значении Front построение фигур производится на переднем плане); FilledPlot [{ fl, f2,...}, {х, xmin, xmax} ] — строит графики функций с выделением областей между ними разной окраской (цвет задается автоматически). Поясним применение этих функций рядом примеров. Перед этим надо не забыть загрузить подпакет командой<< Graphics`FilledPlot`На рис. 14.15 показано построение смещенной по оси у экспоненты с закраской области между линией экспоненты и горизонтальной осью х.

Рис. 14.15. Построение экспоненты с закраской областей между ней и осью абсцисс
Действие функции FilledPlot при построении графиков трех функций показано на рис. 14.16. Здесь использована опция Curves->Front, выводящая построение кривых на первый план, благодаря чему отчетливо видны разделительные линии перекрывающихся областей.
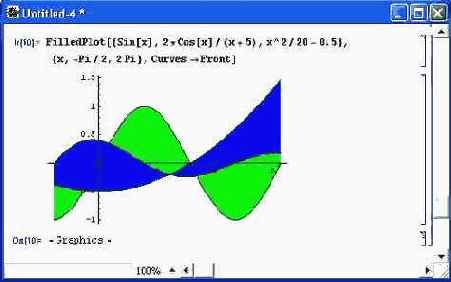
Рис. 14.16. Построение трех кривых с закраской областей между ними и осью абсцисс
Еще один пример построения графиков трех фигур показан на рис. 14.17. Здесь для закраски областей между фигурами и осью абсцисс использована опция Fills и директива GrayLevel (окраска серым цветом заданной плотности). Рисунок 14.18 иллюстрирует закраску областей совместного применения двух функций, одна из которых — корень квадратный из х - 1 — определена только для И > 1. Именно эта область и закрашена.
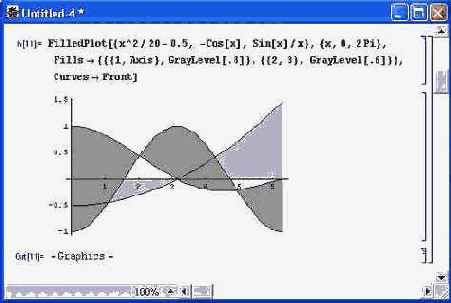
Рис. 14.17. Построение трех кривых с закраской серым цветом
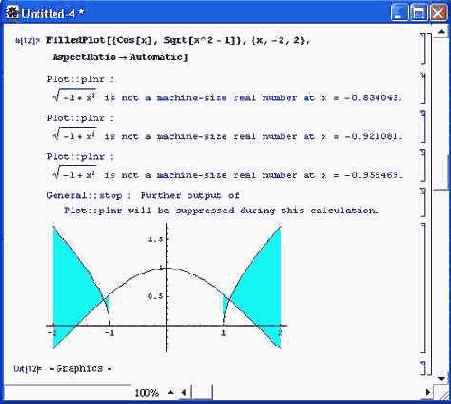
Рис. 14.18. Пример закраски области совместного действия двух функций
Имеется также ряд специальных функций для построения кривых с окраской образуемых ими областей: FilledListPlot [ {yl, у2,...} ] —строит графики с окраской, меняющейся между кривыми {1, y1}, {2, у2 } и осью абсцисс х; FilledListPlot [ {{xl, yl}, {х2, у2},...}] — строит графики ряда кривых с окраской, заданной {xi,yi} и осью абсцисс х; FilledListPlot [datal, data2,...}] — строит графики ряда кривых с закраской областей, специфицированных данными datai. Применение функции FilledListPlot показано на рис. 14.19. Иногда важное значение может иметь опция AxesFront->Значение. При значении этой опции False область закраски закрывает соответствующую часть осей, а при значении True оси выводятся поверх закраски. Сам по себе вывод осей задастся опцией Axes->True. При Axes->False они вообще не выводятся. Рисунок 14.20 поясняет вывод осей и их построение поверх закращениой области. В данном случае область окраски ограничена треугольником, который строится как полигон. Если установить опцию AxesFront->False, то часть осей (внутри треугольника) будет не видна.
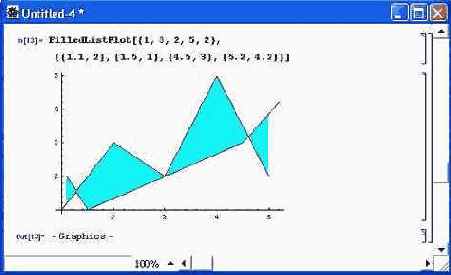
Рис. 14.19. Пример применения функции FilledListPlot

Рис. 14.20. Пример вывода осей поверх закрашенной области
Графики специальных типов — Graphics
Подпакет Graphics задает ряд функций для построения специальных графиков, например с логарифмическими и полулогарифмическими масштабами, с нанесенными на кривые точками, графиков в виде гистограмм и т. д. Такие графики широко применяются для визуализации не только математических и физических, но также финансовых и экономических расчетов. К примеру, функция Log-Plot [f, {х,xmin,xmax}] строит линейно-логарифмический график/(x) при изменении х от xmin до xmax. Список таких функций дан в приложении. Ввиду очевидности этих функций ограничимся одним примером — построением экспоненциальной функции в полулогарифмическом масштабе (по оси у масштаб логарифмический, а по оси х~ линейный). Как видно из рис. 14.21, график вырождается в прямую линию. Для построения графиков в полярной системе координат заданы следующие функции: PolarPlotff, {t, tmin, tmax} ] — строит график функции в полярной системе координат как положение конца радиус-вектора f при изменении угла t от tmin до tmax; PolarPlot [ { f 1, f 2,...}]- строит графики ряда функций f 1, f 2,... в полярной системе координат; PolarListPlot [ {rl, r2,...} ] — строит график списка радиусов ri, равномерно изменяя угловую координату.
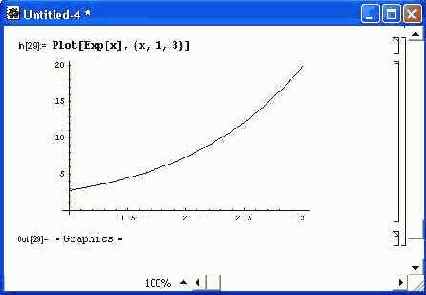
Рис. 14.21. Построение графика экспоненты в полулогарифмическом масштабе
Построение графика трех функций в полярной системе координат с помощью функции PolarPlot представлено на рис. 14.22.

Рис. 14.22. Построение графиков трех функций в полярной системе координат
В ряде случаев удобно представление данных в виде столбцовых и круговых диаграмм. Для построения столбцовых диаграмм служат функции, описанные ниже: BarChart [datalistl,datalist2,...] — строит столбцовую диаграмму по данным списков, располагая столбцы рядом и обеспечивая их автоматическую закраску цветом (рис. 14.23). Здесь любопытно отметить, что списки данных могут иметь разную длину. Число столбцов задается большим списком. Отсутствующие данные у спис- ков меньшей длины считаются нулевыми, и для них столбцы не строятся. Данные, представленные отрицательными числами, строятся как столбцы, обращенные вниз.

Рис. 14.23. Построение столбцовых диаграмм для двух списков данных с расположением столбцов друг рядом с другом
StackedBarChart [datalist1, datalist2,...] — строит столбцовую диаграмму, располагая столбцы одних данных над столбцами других данных (рис. 14.24) с автоматическим выбором цветов для каждого набора данных.

Рис. 14.24. Построение столбцовых диаграмм со столбцами, расположенными друг над другом
В этой столбцовой диаграмме вначале строятся столбцы, представляющие данные для первого списка, над ними надстраиваются столбцы новых данных, так что общая высота столбцов пропорциональна сумме численных значений i-x элементов списков. PercentileBarChart [datalistl, datalist2,...] — строит столбцовую диаграмму, отображающую нормированные данные в процентах (рис. 14.25). Здесь построение идет так же, как в предыдущем случае. Однако высоты столбцов указываются в процентах и нормируются — за 100 % принимается максимальная высота столбцов выше горизонтальной оси, а за -100 % — максимальная высота столбца ниже горизонтальной оси. GeneralizedBarChart [datalistl, datalist2,...] — строит столбцовую диаграмму с заданной высотой и шириной столбцов (рис. 14.26).

Рис. 14.25. Построение столбцовых диаграмм с процентным отсчетом

Рис. 14.26. Построение столбцовых диаграмм с произвольной шириной столбцов
В этом случае имеется возможность указать в списках данных позицию по оси х, высоту столбца и его ширину. Ширина задается в относительных единицах: при ширине, равной 1, столбцы сливаются (но выделяются цветом), при величине меньше 1 они разделяются пустыми промежутками, а при величине, большей 1, столбцы перекрываются. Все указанные функции имеют опции, существенно влияющие на вид диаграмм. Рекомендуется просмотреть их с помощью функции Options. Ограничимся тремя наглядными примерами на применение опций. Рисунок 14.27 показывает построение столбцовой диаграммы с горизонтальным расположением столбцов и произвольным выбором цвета для каждого набора. На рис. 14.28 построена диаграмма для одного комплекта данных. Но выбор цвета каждого из столбцов задается с помощью условного оператора. На рис. 14.29 показан наиболее сложный пример построения столбцовых диаграмм. Наряду с цветовыми эффектами задается обвод пунктирной линией столбцов одного из комплектов данных и, главное, — вывод надписей (названий месяцев) под наборами столбцов. Обратите внимание на то, что надписи могут быть на русском языке.
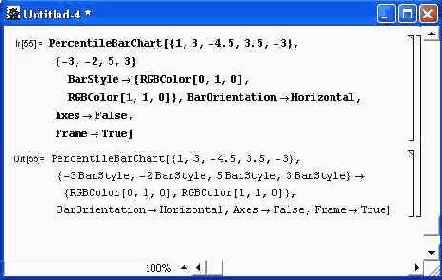
Рис. 14.27. Построение столбцовой диаграммы с горизонтально расположенными столбцами и произвольным выбором цвета для каждого набора данных

Рис. 14.28. Столбцовая диаграмма с выбором цвета столбцов по условию
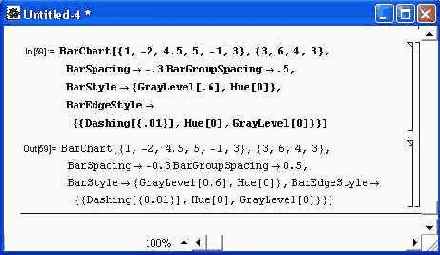
Рис. 14.29. Комплексное построение столбцовых диаграмм
Следующая функция позволяет стоить круговые диаграммы. Они наиболее удобны, когда оцениваются относительные величины, при этом сумма данных соответствует площади круга: PieChart [data] — строит круговые диаграммы по данным data (рис. 14.30). Тип диаграммы задается опциями, список которых и значения по умолчанию можно получить командой Options [PieChart]. Одна из опций— PieExploded — позволяет отделить заданный сектор от диаграммы, что порой повышает наглядность представления данных.

Рис. 14.30. Построение набора круговых диаграмм Здесь использована также одна из следующих функций:
DisplayTogether [plotl,plot2,..., opts] — строит комбинированный графический объект, объединяя графики ploti в общих координатных осях; DisplayTogetherArray [plotl,plot2,..., opts] — строит комбинированный графический объект, выводя графики ploti в виде массива. На рис. 14.31 показано построение круговой диаграммы с применением окраски чередующихся секторов оттенками серого цвета.

Рис. 14.31. Построение круговой диаграммы с раскраской чередующихся секторов оттенками серого цвета
Еще одну возможность разнообразить круговые диаграммы иллюстрирует рис. 14.32. Здесь показано, что в секторы можно заносить небольшие надписи, например имена людей, даты и т. д.

Рис. 14.32. Построение круговой диаграммы с надписями внутри секторов
Функция DisplayTogether позволяет объединять графики разного типа. На рис. 14.33 показано построение графика экспериментальных точек и линий линейной и параболической регрессии.

Рис. 14.33. Совместное построение исходных точек данных и линий линейной и параболической регрессии
Применение функции DisplayTogetherArray для построения трех круговых диаграмм с номерами секторов показано на рис. 14.34. Это те же диаграммы, что и на рис. 14.30, но аргумент функции DisplayTogetherArray на сей раз представляет собой не одномерный, а двумерный массив (в первой строке два графика, во второй — один).

Рис. 14.34. Построение трех круговых диаграмм с номерами секторов
Иногда нужно использовать в качестве точек графика цифры. Это реализует следующая функция, имеющая три формы: TextListPlot [ {y1, у2,...} ] — построение точек с ординатами yi и абсциссами 1, 2, ... с представлением их числами 1, 2, ... (рис. 14.35); TextListPlot [ {{xl, yl}, {х2, у2},...} ] — построение точек с координатами {xi, yi} и представлением их числами 1, 2, ...; TextListPlot [ {{xl, yl, exprl), {x2,y2,expr2 },...}] — построение точек с координатами {xi, yi} и представлением их числами, заданными выражениями expri.

Рис. 14.35. Построение графика сточками, представленными цифрами
Еще одна функция, также имеющая три формы, дает тот же результат, но дополнительно строит и сами точки:LabelListPlot [ {yl, у2,...} ] LabelListPlot [{ {xl,yl}, {х2,у2 },...}] LabelListPlot [{ {x1, y1, expr1}, {х2, у2, expr2 },...}]Наконец, есть еще одна функция: ErrorListPlot [{{yl, dl}, {y2, d2 },...}] — построение графика точек yi с зонами ошибок di (рис. 14.36).
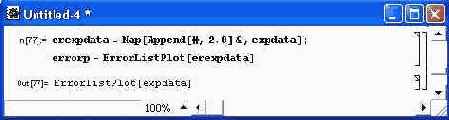
Рис. 14.36. График с точками и зонами ошибок
Таким образом, подпакет Graphics обеспечивает построение наиболее распространенных типов графиков, используемых в научно-технической и финансово-экономической литературе.
Специальные типы трехмерных графиков— Graphics3D
В подпакете Graphics3D, загружаемом командой
<<Graphics`Graphics 3D`имеется ряд программ для простого построения трехмерных графиков. Они описаны ниже с примерами: BarChart3D[ {{ zll, z!2,...},{z21, z22 },...} ] — строит трехмерную столбцовую диаграмму по наборам данных высот столбцов z 11 , z п , ... (рис. 14.37); BarChart3D[ {{{zll, stylell}, {z21, style21},...} ] — строит трехмерную столбцовую диаграмму по наборам данных высот столбцов z u , z vl , ... с указанием спецификации стиля для каждого столбца. Нетрудно заметить, что функция BarChartSD автоматически задает стиль и цвет построения столбцов диаграммы. Эта функция имеет массу опций, с помощью которых можно менять вид диаграммы (рис. 14.38). Как обычно, перечень опций можно вывести с помощью команды Options [BarChart3D].

Рис. 14.37. Построение трехмерной столбцовой диаграммы

Рис. 14.38. Вариант диаграммы с черно-белой раскраской
Scatter Plot 3D [{ {x1, yl, zl}, {х2, у2, z2 },...}] — строит точки в пространстве по их заданным координатам. При использовании опции Plot-Joined->True точки соединяются отрезками прямых, и строится линия в пространстве (рис. 14.39).
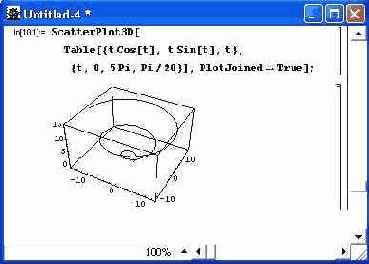
Рис. 14.39. Построение пространственной кривой по точкам
Обратите внимание на то, что список точек формируется с помощью функции Table. Это возможно, когда построение делается для аналитически заданной функции, описывающей трехмерную поверхность. ListSurfacePlot3D[{ { {x11, y11, zll}, {x12, y12, z13},...} } }] - строит трехмерную поверхность по координатам ее точек-(рис. 14.40).

Рис. 14.40. Построение трехмерной поверхности по координатам ее точек
Здесь список координат точек также задаются функцией Table. Выбором диапазона изменения значений переменных х, у и z можно добиться различных эффектов, например изображения только части сферы (на рис. 14.40, к примеру, показано построение полусферы). Следующие функции дают построения с проекциями: ShadowPlot3D [f, {х, xmin, xmax}, {у, ymin, углах} ] — строит график поверхности f(z, y) с ее проекцией на опорную плоскость (рис. 14.41); ListShadowPlot3D[{{ {xll, yll, zll}, {x!2, y!2, z!3},...}} }] -строит график поверхности z(x, у) с ее проекцией на опорную плоскость по координатам точек поверхности.

Рис. 14.41. Построение графика трехмерной поверхности и ее проекции на опорную плоскость
Еще один простой и эффектный пример применения функции ShadowPlot3D показан на рис. 14.42. Здесь изображение поверхности — пика — проецируется на верхнюю плоскость, что дает наглядное представление о построенной фигуре.
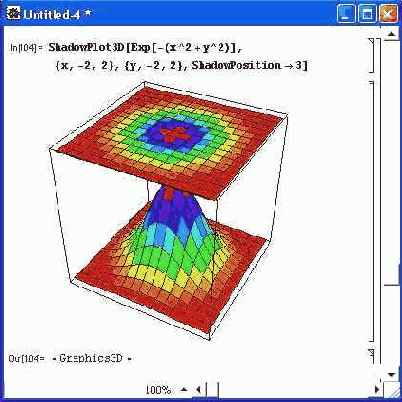
Рис. 14.42. Построение фигуры — пика — и ее проекции на верхнюю плоскость
С помощью функции Shadow [go], где до — графический объект, представляющий трехмерную фигуру, можно построить и более сложные рисунки — например, график объемной фигуры и сразу всех трех ее проекций на взаимно перпендикулярные плоскости. Такое построение иллюстрируется документом, показанным на рис. 14.43. С функцией Shadow можно использовать различные опции. Отметим наиболее существенные — XShadow, YShadow и ZShadow. Например, задав Zshadow-> False, можно удалить одну из проекций, плоскость которой перпендикулярна оси z. Для получения проекций на заданную плоскость, расположенную в пространстве, служат следующие функции: Project [g,pt] — дает проекцию объекта g на плоскость, нормаль которой задана списком из трех элементов pt. Например, список {1,1,0} даст проекцию на диагональную плоскость; Project[g, {e1,e2},pt] — дает проекцию объекта g в плоскости, определенной векторами {el,e2}, выходящими из точки с координатами pt (рис. 14.44); Project[g, {e1, e2 } ,pt, origin] — то же, но направление проецирования определяется точками pt и origin. В конце подпакета определена функция StackGraphics [ {gl, g2,...}], которая строит двумерные графические объекты, располагая их каскадно, то есть разнося в пространстве по третьей координате (рис. 14.45).

Рис. 14.43. Построение объемной фигуры и всех трех ее проекций

Рис. 14.44. Пример построения проекции но заданной плоскости
Обратите внимание на то, что здесь каждая синусоида расположена на своей плоскости.

Рис. 14.45. Пример построения трех синусоид, расположенных каскадно
Построение графиков неявных функций — ImplicitPlot
Подпакет ImplicitPlot задает три варианта функции для построения графиков неявно заданных функций: ImplicitPlot [eqn, {x, xmin, xmax} ] — построение функции, неявно заданной уравнением eqn, при х, меняющемся от xmin до xmax; ImplicitPlot [eqn, {x, xmin,ml,m2,..., xmax} ] — построение функции, неявно заданной уравнением eqn, при х, меняющемся от xmin до xmax с исключением точек m1, m2, ...; ImplicitPlot [ {eqnl, eqn2,...}, ranges, options] — построение функций, неявно заданных уравнениями eqni, при х, меняющемся в пределах ranges и при задании опций options. Примером может быть функция х 2 + k у 2 = r 2 , задающая построение эллипса. На рис. 14.46 показано такое построение. Вторая форма задания функции иллюстрируется рис. 14.47. Здесь строится сразу целое семейство эллипсов. И, наконец, на рис. 14.48 показано применение третьей формы функции ImplicitPlot с использованием опции PlotStyle и директивы Dashing.
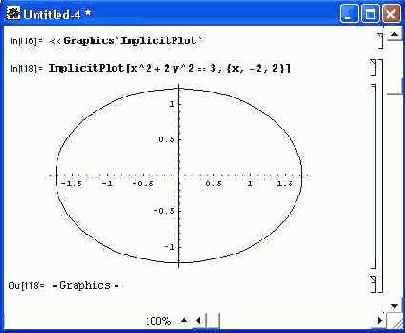
Рис. 14.46. Построение эллипса по неявному выражению

Рис. 14.47. Построение семейства эллипсов по их уравнениям

Рис. 14.48. Пример применения функции ImplicitPlot с опцией PlotStyle
Вывод обозначений кривых— Legend
Наглядность графиков, особенно имеющих несколько кривых, повышается при выводе обозначений кривых — так называемой легенды. В подпакете Legend для этого имеются следующие средства:
PlotLegend->{textl,text2,...} — опция для функции Plot, устанавливающая легенду в виде последовательных текстовых надписей (рис. 14.49); ShowLegend [graphic, legendl, Iegend2,...] — добавляет легенду в имеющийся график graphic; {{{boxl, textl},...}, opts} — спецификация легенды с цветными примитивами или графиками для рамок boxi с текстами texti; {colorfunction, n, ninstring,maxstring, opts} — спецификация легенды с n рамками, указанием цветовой спецификации и строк, размещаемых в рамках.

Рис. 14.49. Пример построения графиков двух функций с выводом легенды
Обратите внимание на то, что среди многочисленных опций функции Plot имеется ряд, относящихся к параметрам легенды: LegendPosition-> {-1,1} — установка позиции легенды, LegendSize->Automatic — установка размера легенды, LegendShadow->Automatic — установка тени для рамки легенды, Legend-Orientation->Vertical — ориентация рамки легенды, LegendLabel->None — заголовок легенды и LegendTextDirection->Automatic — направление текста. С помощью этих опций можно существенно влиять на вид легенды. На рис. 14.50 показано построение графика плотности с применением функции ShowLegend для вывода легенды в виде таблицы плотностей. Обратите внимание на применение опции LegendPosition для вывода легенды справа от графика.
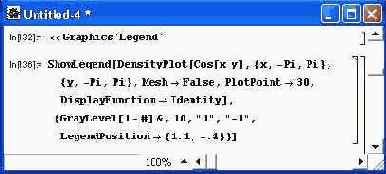
Рис. 14.50. Построение графика плотности с легендой
Для иллюстрации эффективности применения опций функции Plot, влияющих на вид легенды, рассмотрим еще один пример, представленный на рис. 14.51.

Рис. 14.51. Пример построения графика двух функций с легендой и установкой ряда ее опций
В заключение отметим еще две функции подпакета Legend: Legend [legendargs, opts] — создает графический примитив для задания индивидуальной легенды; ShadowBox [pos, size, opts] — создает графический примитив в виде рамки для легенды. К примеру, показанный ниже вызов функции ShadowBox создает графический примитив в виде пустой рамки с тенью: ShadowBox[{0, 0}, {1, 1},ShadowBackground -> GrayLevel[.8]] {GrayLevel[0.8], Rectangle[{0.1, -0.1), {1.1, 0.9}], GrayLevel[l], Rectangle[{0, 0}, {1, 1}], Thickness[0.001], GrayLevel[0], Line[{{0, 0), {1, 0), {1, 1}, {0, 1), {0, 0}}]} Для просмотра полученной рамки можно использовать команду Show[Graphics[%]] Применение функции Graphics здесь связано с тем, что ShadowBox порождает графический примитив, а не законченный графический объект.Построение графиков с множеством объектов — MultipleListPlot
В подпакете MultipleListPlot содержится расширенный вариант встроенной функции ListPlot: MultipleListPlot [listl, Iist2,...] — строит множество графических объектов по данным списков. Списки могут быть представлены ординатами у, координатами точек {х,у), в виде {point, ErrorBar [ {negerr,poserr} ] } и т.д.

Рис. 14.52. Создание трех списков значений функций и их построение
Рисунок 14.52 иллюстрирует создание трех списков — 11, 12 и 13 — для трех функций и вывод их графиков в виде различных маленьких фигур. Особое значение имеет опция Plot Joined. Если она используется в виде Plot-Joined->True, то это означает соединение точек на графиках отрезками линий разного стиля, выбираемого автоматически (рис. 14.53).

Рис. 14.53. Графики трех функций, построенные линиями, соединяющими их точки
Эта опция может быть представлена и со значением в виде списка. Например, ее применение в виде PlotJoined->{True, False, False} означает, что точки первой кривой соединяются линиями, тогда как точки второй и третьей кривых линиями не соединяются. Рисунок 14.54 поясняет этот способ построения графиков.

Рис. 14.54. Построение трех графиков, только у одного из которых точки соединены линиями
Функция MultipleListPlot может использовать в списках указания на построение точки с зоной погрешности (ErrorBar). Этот случай иллюстрирует рис. 14.55. Более интересный случай построения точек с двумерными зонами погрешности в виде окружностей или эллипсов демонстрирует рис. 14.56.

Рис. 14.55. Построение точек с одномерными зонами погрешности

Рис. 14.56. Построение точек с двумерными зонами погрешности
Следующие функции служат для вывода символов в качестве точек: PlotSymbol [type] — задает тип символа (возможные значения: Box, Diamond, Star или Triangle). Возможно применение опции_ Filled-> False; PlotSymbol [type, size] — задает тип символа и его размер size; MakeSymbol [primitives] — задает вывод символа, создаваемого графическим примитивом. Рисунок 14.57 показывает построение точек с применением графических примитивов. Этот путь позволяет обозначать точки графиков практически любыми фигурами.

Рис. 14.57. Построение точек с применением графических примитивов
Для создания примитивов в виде правильных многоугольников (полигонов) используется директива RegularPolygon: RegularPolygon [n] — правильный «-угольный полигон; RegularPolygon [n, rad] — правильный и-угольный полигон с заданным радиусом описанной окружности rad; RegularPolygon [n, rad, ctr] — то же с заданным центром ctr; RegularPolygon [n, rad, ctr, tilt] — то же с углом поворота фигуры на tilt градусов; RegularPolygon [n, rad, ctr, titl, k] — соединение линиями через k вершин. Рисунок 14.58 показывает построение полигона — семиугольника с радиусом 3, центром в точке {0, 0}, углом поворота 20° и соединением через 3 вершины (попробуйте задать этот параметр другим целым числом и убедитесь, насколько меняется форма фигуры). Директивы Dashing[ {Dot, Dash, LongDash,...} ] и AbsoluteDashing[ {Dot,...} ] служат для спецификации типа линий графиков. На рис. 14.59 представлены примеры такой спецификации и построения отрезков прямой линиями разных типов. Применение функций подпакета MultipleListPlot наиболее ценно при визуализации математических расчетов, где преобладают графики тех типов, которые создаются этими функциями.

Рис. 14.58. Построение полигона

Рис. 14.59. Примеры построения отрезков прямых разными стилями
Построение 3D-параметрических графиков — ParametricPlot3D
Трехмерные графики с параметрически заданными функциями, описывающими положение их точек, относятся к числу наиболее сложных, но в то же время весьма эффектных. В подпакете ParametricPlotSD определены функции, упрощающие подготовку таких графиков:
ParametricPlot3D[{fx,fy,fz},{u,u0,ul,du},{v,c0,vl,dv}] — строит трехмерную поверхность, заданную параметрически функциями f x, f у и f z от переменных и и v с заданными диапазонами изменения и приращениями du и dv (рис. 14.60); PointParametricPlot3D[ { fx, f у, f z},{u,u0,ul,du}] — строит точками трехмерную поверхность, заданную параметрически функциями fx, f у и f z от одной переменной и с заданным диапазоном изменения и приращением du; PointParametricPlot3D[{fx,fy,fz},{u,u0,ul,du),{v,c0,vl,dv}] — строит точками трехмерную поверхность, заданную параметрически функциями fx, f у и f z от переменных и и v с заданными диапазонами изменения и приращениями du и dv.

Рис. 14.60. Пример построения сферы с вырезом с помощью функции ParametricPlot3D
Обратите внимание на то, что выбором диапазона изменения углов можно получить вырез сферы. Окраска поверхности осуществляется автоматически. На рис. 14.61 показан пример применения функции PointParametricPlotSD. Здесь сфера построена отдельными точками. Для построения трехмерных поверхностей в сферической и цилиндрической системах координат служат следующие функции: SphericalPlot3D[r, {t, trnin, tmax}, {p,pmin,pmax} ] — построение графика в сферической системе координат; CylindricalPlot3D[z,{t,tmin,tmax},{p,pmin,pmax}] — построение графика в цилиндрической системе координат. На рис. 14.62 показано построение усеченной сверху сферы с помощью функции SphericalPlot3D. Нетрудно заметить, что применение данной функции — самый простой способ построения сферы. Это естественно, поскольку система координат сферическая.

Риc. 14.61. Пример построения сферы точками
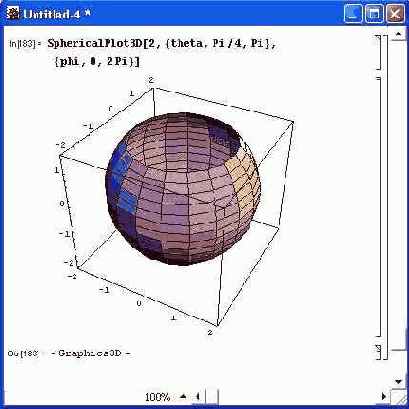
Рис. 14.62. Пример построения сферы с помощью функции SphericolPlot3D
Пример построения поверхности, напоминающей по виду «тарелку» спутниковой антенны, в цилиндрической системе координат дан на рис. 14.63. С помощью опции Viewpoint можно изменять положение точки, с которой рассматривается фигура. Это существенно меняет ее вид (рис. 14.64). Еще раз напоминаем, что интерфейс Mathematica предусматривает изменение точки просмотра уже построенной фигуры. При этом Mathematica 4 позволяет вращать фигуру мышью. Рекомендуется просмотреть список опций данных функций, позволяющих в широких пределах менять вид и стиль построения графиков.
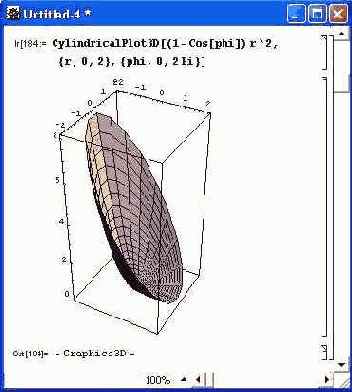
Рис. 14.63. Пример построения поверхности в цилиндрической системе координат

Рис. 14.64. Пример построения фигуры, видимой из заданной точки просмотра
Представление полей на плоскости — PlotField
В подпакете PlotField имеются функции, позволяющие строить стрелками графики полей: PlotVectorField[ {fx, f у}, {x, xmin, xmax), {y, ymin, ymax} ] —строит плоскость из векторов (стрелок), ограниченную пределами изменения х и у; PlotGradientField[f,{x,xmin,xmax},{у,ymin,ymax}] — строит плоскость из векторов (стрелок) градиента функции f, ограниченную пределами изменения х и у; PlotHamiltonianField[f,{x,xmin,xmax},{у,ymin,ymax}] — строит плоскость из векторов (стрелок) гамильтониана функции f, ограниченную пределами изменения х и у; PlotPolyaField[f, {х,xmin,xmax}, {у, ymin, ymax} ] — представляет график комплексной функции f(x, у). Рисунок 14.65 показывает применение функции PlotVectorField для построения векторного поля согласно параметрически заданной на плоскости функции.

Риc. 14.65. График векторного поля на плоскости
Еще один пример (рис. 14.66), иллюстрирует построение градиента поля с помощью функции PlotGradientField. Применение функции PlotHamiltonianField демонстрирует рис. 14.67. Указанные функции имеют множество опций. Отметим основные из них (в качестве значений приведены значения по умолчанию): ScaleFactor->Automatic — устанавливает размер векторов (стрелок); ScaleFunction->None — устанавливает функцию, вычисляющую размер стрелок; MaxArrowLenght->None — устанавливает ограничение длины стрелок; ColorFunction->None — задает функцию цвета; PlotPoints->15 — задает число точек по координатам для построения стрелок.

Рис. 14.66. График градиента поля

Риc. 14.67. Пример применения функции PlotHamiltonianField
Пример построения сложного графика с применением шестнадцати узловых точек по каждому направлению и использованием опции ScaleFunction показан на рис. 14.68. Работу функции PlotPolyaField поясняет рис. 14.69. Обратите внимание на то, что функция в данном случае комплексная.
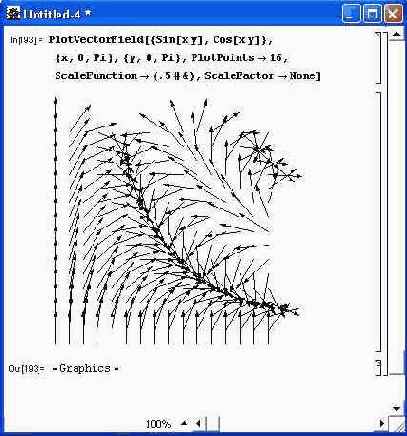
Рис. 14.68. Пример графика поля с применением нескольких опций

Рис. 14.69. Пример графика поля для комплексной функции
Применение опций позволяет строить самые разнообразные графики различных полей — тепловых, гравитационных, электрических и др. В подпакете PlotField есть еще одна функция, представляемая в двух формах: ListPlotVectorField [ {{vect 11, vect12,...},{vect21, vect22,...},...} ] — строит график векторного поля прямоугольного массива векторов vect xy ; ListPlotVectorField [{{pt1, vect1,...}, (pt2,vect2,...},...}] —строит график векторного поля по списку векторов vect xy , расположенных в точках pti. Применение этой функции поясняет график, представленный на рис. 14.70.

Рис. 14.70. Пример построения графика векторного поля с помощью функции ListPlotVectorField
Приведенных примеров вполне достаточно, чтобы судить о возможностях подпа-кета PlotField. В справочной базе данных можно найти другие примеры построения графиков векторных полей.Представление полей в пространстве — PlotField3D
Для представления векторных полей в пространстве служат функции подпакета PlotField3D: PlotVectorField3D[{fx,fy,fz},{x,xmin,xmax},{y,ymin, ymax}, {z, zmin, zmax} ] — строит график векторного поля параметрически заданной трехмерной фигуры; PlotGradientField3D[{fx,fy,fz},{x,xmin,xmax},{y,ymin,ymax}, {z, zmin, zmax} ] — строит график градиента векторного поля параметрически заданной трехмерной фигуры. Эти функции подобны описанным в предшествующем разделе, но используются для построения векторных полей не на плоскости, а в пространстве. Рисунок 14.71 показывает пример такого построения. Как видно из рис. 14.71, векторное поле строится отрезками прямых, а не стрелками. Последнее связано с тем, что по умолчанию задана опция VectorHeads-> False. Изменив ее на VectorHeads->True, можно получить представление векторного поля направленными стрелками. Кроме того, используя опцию Plot-Points->n, можно получить заданное число стрелок п по всем направлениям графика. Все это учтено на графике, представленном на рис. 14.72.

Рис. 14.71. Пример построения графика векторного поля в пространстве отрезками прямых

Рис. 14.72. Пример построения графика градиента поля направленными стрелками
В подпакете PlotFieldSD имеется еще одна функция: ListPlotVectorField3D[{ {ptl, vectl}, {pt2, vect2 },...} ] -строит график векторного поля в пространстве по данным векторов vecti, расположенных в точках pti. Рисунок 14.73 поясняет применение этой функции.

Рис. 14.73. Пример построения графика векторного поля функцией ListPlotVectorReld3D
Нетрудно заметить, что при большом числе векторов в пространстве графики этого типа теряют наглядность. Рекомендуется тщательно отлаживать их, используя весь набор опций (как его получить, описывалось неоднократно).
Построение полиэдров — Polyhedra
Подпакет Polyhedra служит для создания регулярных пространственных фигур — полиэдров. Они задаются как графические примитивы и выводятся функцией Show:
Show [Polyhedron [polyname] ] — строит полиэдр с именем polyname в центре графика; Show[Polyhedron[polyname,{х,у,z},scale]] — строит полиэдр с именем polyname с центром в точке {х, у, z} и параметром масштаба scale. Возможно задание следующих имен полиэдров: Tetrahedron, Cube, Octahedron, Dodecahedron, Icosahedron, Hexahedron, GreatDodecahedron, Small-StellatedDodecahedron, GreatStellatedDodecahedron и Greatlcosa-hedron. Пример построения полиэдра Icosahedron показан на рис. 14.74.

Рис. 14.74. Построение полиэдра Icosahedron
Возможность вывода с помощью функции Show двух полиэдров иллюстрирует рис. 14.75.

Рис. 14.75. Вывод функцией Show двух полиэдров
Для вывода полиэдров служит также ряд описанных ниже функций. Так, для построения звездчатых форм полиэдров предназначена функция Stellate: Show [Stellate [Polyhedron [polyname] ] — построение звездчатых форм полиэдров; Show[Stellate[Polyhedron[polyname], ratio] — построение звездчатых форм полиэдров с заданным отношением радиусов описанной и вписанной сфер ratio. Рисунок 14.76 показывает построение звездообразного (или игольчатого) полиэдра. Представленная фигура напоминает некоторых морских животных — ежей и звезд.
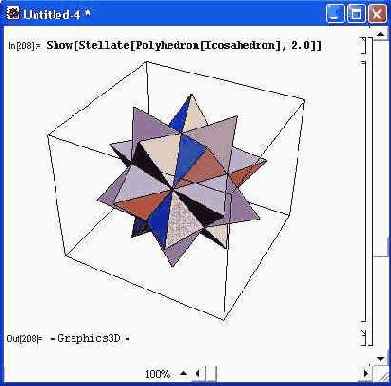
Рис. 14.76. Построение звездчатой формы полиэдра
Полиэдры, применяемые в геодезии, можно получить с помощью следующей функции: Show [Geodesate [Polyhedron [polyname], n] — построение полиэдра с вершинами, лежащими на сфере, представляющего собой результат я-кратно-го разбиения на треугольники граней полиэдра polyname; Show [Geodesate [Polyhedron [polyname] , n, {x, y, z}, radius] —построение полиэдра с вершинами, лежащими на сфере с заданным положением центра {x,y,z} и радиусом radius, представляющего собой результат п-кратного разбиения на треугольники граней полиэдра polyname. Рисунок 14.77 показывает применение этой функции. Для построения усеченных полиэдров предназначены следующие функции: Show [Truncate [Polyhedron [polyname] ] ] — построение усеченных полиэдров; Show [Truncate [Polyhedron [polyname], ratio] — построение усеченных полиэдров с заданным коэффициентом усечения ratio (от 0 до 0.5); Show[OpenTruncate[Polyhedron[polyname]]] — построение полиэдров с открытым усечением; Show[OpenTruncate[Polyhedron[polyname], ratio] — построение полиэдров с открытым усечением и заданным коэффициентом усечения ratio (от 0 до 0.5).
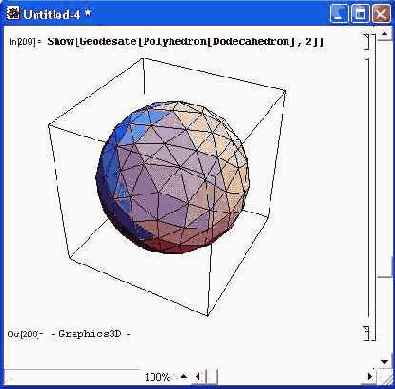
Рис. 14.77. Построение полиэдра в виде сферы
Рисунок 14.78 показывает построение усеченного полиэдра Усечение сделано так, будто полиэдр заполнен материалом. Поэтому усеченные области выглядят как дополнительные грани. Параметр ratio, задающий степень усечения, может иметь значения от 0 до 0.5 (в ином случае выводятся сообщения об ошибке в задании параметра).
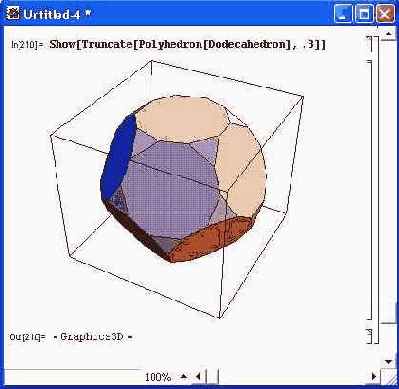
Рис. 14.78. Построение усеченного полиэдра
Усечение может быть открытым — такой вариант реализуется функцией со словом Open в имени. В этом случае фигура выглядит так, будто она склеена из тонкого картона (рис. 14.79). При этом в местах усечения фигура прозрачна.
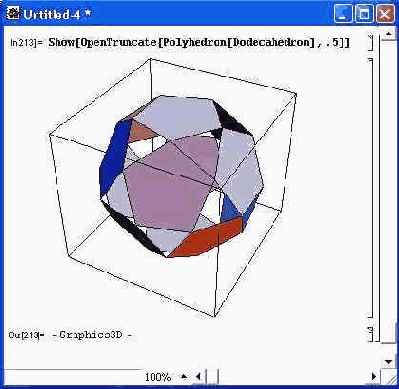
Рис. 14.79. Построение усеченного полиэдра с открытыми местами усечения
В заключение этого раздела отметим следующие функции: First [Polyhedron [polyname] ] — возвращает список полигонов для указанного полиэдра; Vertices [polyname] — возвращает список координат вершин полиэдра; Faces [polyname] — возвращает список вершин, ассоциированных с каждой гранью. Они ничего не строят, а лишь возвращают специфические параметры полиэдров. Примеры применения этих функций представлены ниже:First[ Polyhedron[ Octahedron ]] {Polygon[{{0, 0, 1.41421}, {1.41421, 0, 0}, {0, 1.41421, 0}}], Polygon[{{0, 0, 1.41421}, {0, 1.41421, 0}, {-1.41421, 0, 0}}], Polygon[{{0, 0, 1.41421}, {-1.41421, 0, 0}, {0, -1.41421, 0}}], Polygon[{{0, 0, 1.41421}, {0, -1.41421, 0}, {1.41421, 0, 0}}], Polygon[{{1.41421, 0, 0}, {0, -1.41421, 0}, {0, 0, -1.41421}}], Polygon[ {{1.41421, 0, 0}, {0, 0, -1.41421}, {0, 1.41421, 0}}], Polygon[{{0, 0, -1.41421}, {0, -1.41421, 0}, {-1.41421, 0, 0}}], Polygon[{{0, 1.41421, 0}, {0, 0, -1.41421}, {-1.41421, 0, 0}}]} Vertices[ Octahedron ] {{0, 0, 1.41421}, {1.41421, 0, 0}, {0, 1.41421, 0}, {0, 0, -1.41421}, {-1.41421, 0, 0}, {0, -1.41421, 0}} Faces[ Octahedron ] {{1, 2, 3}, {1, 3, 5}, {1, 5, 6}, {1, 6, 2}, {2, б, 4}, {2, 4, 3}, {4, б, 5}, {3,4,5}}Приведенные выше функции можно использовать на занятиях по стереометрии, где полученные с их помощью фигуры могут прекрасно иллюстрировать теоретические положения курса.
Создание графических форм — Shapes
Нередко желательно придать трехмерным объектам определенную форму, например кольца или бублика. Некоторые возможности для этого дают функции под-пакета Shapes. Основной из них является функция Show [Graphics3D [shape] ], которая производит отображение формы со спецификацией shape. С ней могут использоваться графические примитивы: Cone [r, h, n] — конус с основанием радиуса r и высотой h на основе n-сто-роннего полигона; Cylinder [r, h, n] — цилиндр радиуса r и высотой h на основе и-стороннего полигона; Torus[rl,r2,n,m] — объемное кольцо с внешним и внутренним радиусами rl и г 2 и числом сторон каркаса n и m; Sphere [r, n,m] — сфера радиуса г, составленная из многоугольников с параметрами n и m и числом сторон п(т - 2) + 2; MoebiusStrip [rl, r2, n] — кольцо Мебиуса с радиусами rl и r2, построенное на основе полигона с 2n сторонами; Helix[r,h,m,n] — плоская спираль радиусом г и высотой h c m витками на основе поверхности, разбитой на nxm четырехугольников; DoubleHelix[r,h,m,n] — плоская двойная спираль радиусом r и высотой h с m витками на основе поверхности, разбитой на nxm четырехугольников. Возможно указание фигур без параметров. Это означает, что они выбираются по умолчанию следующими:Соnе[1, 1, 20] Cylinder[1, 1, 20] Helix[l, 0.5, 2, 20] DoubleHelix[l, 0.5, 2, 20] MoebiusStrip[1, 0.5, 20] Sphere[l, 20, 15] Torus[l, 0.5, 20, 10]На рис. 14.80 показан пример построения фигуры DoubleHelix без указания ее параметров с помощью функций Show и GraphicsSD. Рисунок 14.81 показывает построение другой фигуры — кольца Мебиуса с указанием параметров фигуры. Обратите внимание на то, что в обоих случаях автоматически обеспечивается функциональная окраска фигур, облегчающая их восприятие.
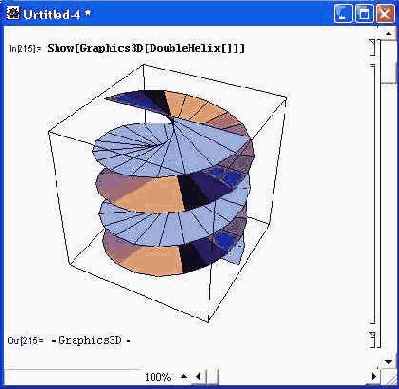
Рис. 14.80. Пример построения фигуры без указания параметров

Рис. 14.81. Построение кольца Мебиуса
Для преобразования графических объектов в подпакете Shapes имеются следующие функции: RotateShape [g,phi, theta,psi] — поворот графического объекта на углы phi, theta и psi; TranslateShape [g, {х, у, z} ] — сдвиг графического объекта на расстояния {х,у, z}; Af fineShape [g, {scalel, svale2, scaleS} ] — умножение всех координат объекта g на указанные множители. Рисунок 14.82 иллюстрирует осуществление вращения для кольца Мебиуса. Эффект вращения хорошо заметен, если сравнить положения фигуры на рис. 14.81 и 14.82.

Рис. 14.82. Кольцо Мебиуса после поворота
Функции Show и Graphics3D позволяют строить трехмерные фигуры, которые пересекаются в пространстве. Пример такого построения приведен на рис. 14.83. Нетрудно заметить, что линии пересечения строятся с точностью до одной ячейки — полигона. Поэтому для получения качественных фигур надо увеличивать число полигонов, из которых фигуры синтезируются. Это, однако, увеличивает время построения фигур — оно становится заметным даже при работе на современных компьютерах с процессорами Pentium II и Pentium III.

Рис. 14.83. Фигуры, пересекающиеся в пространстве
В заключение этого раздела отметим, что функция WireFrame [g] дает «каркас» графического объекта, то есть делает все его грани прозрачными. Применение этой функции иллюстрирует пример, показанный на рис. 14.84.
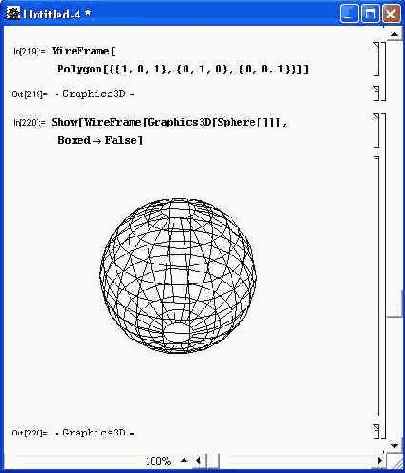
Рис. 14.84. Пример применения функции WireFrame для построения каркаса сферы
Примитивы, использующие сплайны — Spline
Подпакет Spline вместе с уже описанным подпакетом NumericalMath'SplineFit' (сплайновая регрессия) обеспечивает представление данных с помощью сплайна. В подпакете Spline определена единственная функция Spline [points, type], которая создает графический примитив, представляющий сплайн-кривую типа type (Cubic, Bezier или CompoziteBezier — см. описание подпакета NumericalMath'SplineFit').
Среди ее опций важно отметить следующие (как и ранее, приведены значения, используемые по умолчанию): SplineDots->None, SplinePoints->25, Max-Bend->10.0 и SplineDivision->20.0. Рисунок 14.85 показывает задание массива из пяти точек на плоскости и соединение их отрезками прямых и кубическими сплайн-функциями. Хорошо видна аналогия сплайна с гибкой линейкой. Сплайн-функции в данном случае применяются в порядке задания точек в списке pts. В этом случае возможно создание замкнутых линий (рис. 14.85 является наглядным примером этого). Следует отметить, что хотя сплайн-аппроксимация дает хорошие результаты при умеренном числе точек, при малом их числе и неудачном выборе типа сплайнов результат может оказаться неудовлетворительным. Рисунок 14.86 иллюстрирует такую ситуацию. Рисунок 14.87 показывает возможность построения сплайн-функции вместе с точками, через которые она проходит.

Рис. 14.85. Пример интерполяции пяти точек отрезками прямой и сплайнами

Рис. 14.86. Пример срыва сплайн-интерполяции точек

Рис. 14.87. Построение исходных точек и проходящей через них сплайн-функции
Создание поверхностей вращения — SurfaceOfRevolution
Одна из задач компьютерной графики — создание поверхностей вращения. Средства для этого дает подпакет SurfaceOfRevolution. Они представлены следующими функциями: SurfaceOfRevolution [f, {x, xmin, xmax} ] — строит поверхность, образованную вращением кривой, описанной функцией f, при изменении х от xmin до xmax, в плоскости ху; SurfaceOfRevolution [{fx, f у}, {t, tmin, tmax} ] — строит поверхность, образованную вращением кривой, описываемой параметрически заданной на плоскости функцией {f x, f у}, в плоскости xz при изменении параметра t от tmin до tmax; SurfaceOfRevolution[{fx,fy,fz},{t,tmin,tmax}] — строит поверхность, образованную вращением кривой, описываемой параметрически заданной в пространстве функцией {fx, fy, fz}, в плоскости xz при изменении параметра t от tmin до tmax; SurfaceOfRevolution[f,{{x,xmin,xmax},{theta,thetamin,thetamax}}] — строит поверхность вращения кривой, описываемой функцией f, при угле theta, меняющимся от thetamin до thetamax. Рисунок 14.88 дает простой пример построения поверхности, образованной линией cos(x) при изменении х от 0 до 4л, вращающейся вокруг оси xz. Построение задано функцией SurfaceOfRevolution [f, {x, xmin, xmax} ]. В этом случае линия вращается в пределах угла от 0 до 2-я, поэтому поверхность получается круговой.

Рис. 14.88. Фигура, образованная вращением линии cos(x)
Следующий пример показывает ту же фигуру (рис. 14.89) в другом положении. Это достигается сменой угла обзора с помощью опции viewVertical.

Рис. 14.89. Фигура рис. 14.88 в другом положении
Пример применения функции SurfaceOfRevolutibn [ {fx, fy}, {t, tmin, tmax) ] представлен на рис. 14.90. Формируется этакое декоративное яйцо на подставке. Заменив в определении функции Cos [u] на Sin [u], можно получить изображение рюмки.

Рис. 14.90. Построение декоративного яйца на подставке
Рисунок 14.91 демонстрирует возможность построения объемной фигуры с вырезами. Все, что для этого надо, — удачно выбрать диапазон изменения угла вращения. Если он будет от 0 до 2л, то фигура будет сплошной, не содержащей вырезов.

Рис. 14.91. Построение яйца с вырезом
Для управления положением оси вращения служат следующие опции: RevolutionAxis->{x, z } — задает поворот вокруг оси, соединяющей начало координат с точкой {х, z} в плоскости xz\ RevolutionAxis-> {х, у, z} — задает поворот вокруг оси, соединяющей начало координат с точкой {х, у, z}. Рисунок 14.92 иллюстрирует применение опции RevolutionAxis->{x, у, z }. Следующая функция позволяет построить фигуру вращения, образующая линия которой задается массивом точек: ListSurfaceOfRevolution [ {point1,point2,...} ] — создает поверхность вращения, заданную массивом точек pointl, point2, ...; ListSurfaceOfRevolution[{point1,point2,...}, {theta,thetamin,thetamax}] — создает поверхность вращения, заданную массивом точек, при угле вращения theta от thetamin до thetamax. Рисунок 14.93 показывает задание массива точек с помощью функции Table и фигуру вращения, полученную при использовании функции ListSurfaceOf-Revolution во второй форме.

Рис. 14.92. Управление положением оси вращения
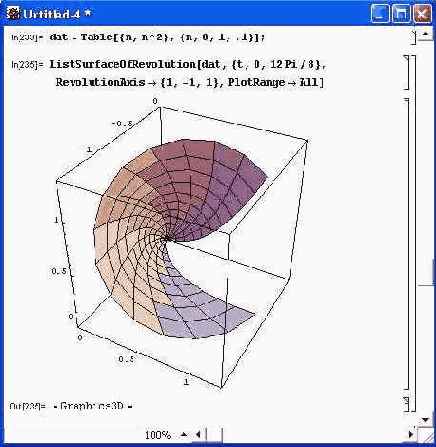
Рис. 14.93. Пример построения фигуры вращения с образующей, заданной массивом точек
Что еще есть в пакете расширения Graphics
Помимо уже рассмотренных подпакетов пакет расширения Graphics содержит подпакеты ThreeScript и Common. Подпакет ThreeScript содержит функцию преобразования трехмерных графических объектов в программный код формата 3-Script, например:<<Graphics 'ThreeScript' obj = Graphics3D[Polygon[0,0,0, 0,1,0, 0,1,1]] • GraphicsSD • ThreeScript[ "object.ts", obj] object.ts !!object.ts % Graphics3D objects boundingbox 0 0 0 0 1 1 viewpoint 1.3 -2.399999999999999 2. ambientlight 000 lightsources 1. 0. 1. 1 0 0 1. 1. 1. 0 1 0 0. 1. 1. 0 0 1 polygon 0 0 0 0 1 0 0 1 1Подпакет Common содержит просто перечень системных символов (точнее, слов), которые приняты во всех подпакетах пакета Graphics. Вот этот список: Horizontal, MaxArrowLength, ScaleFactor, ScaleFunction и Vertical. В этом уроке мы научились: Выполнять анимацию графиков различного типа. Управлять цветами графиков. Строить стрелки на графиках. Строить графики комплекснозначных функций. Строить объемные контурные графики. Строить графики с окраской внутренних областей. Строить графики специальных типов. Строить графики неявных функций. Выводить обозначения кривых — легенды. Строить графики с множеством объектов. Строить параметрические трехмерные графики. Представлять поля на плоскости и в пространстве. Строить объемные многогранники — полиэдры. Создавать графические формы. Работать с примитивами, использующими сплайны. Создавать поверхности вращения.