Разложение функций в ряды

Разложение функций в ряды Тейлора и Маклорена

Одна из широко распространенных математических задач представления данных — разложение заданной аналитической функции в степенной ряд Тейлора относительно некоторой узловой точки с абсциссой хО. Такой ряд нередко проще самой функции (в том смысле, что не требует вычисления даже элементарных функций и вычисляется с помощью только арифметических операций) и дает единообразное представление для разлагаемых функций в виде обычных степенных многочленов.

Большинство достаточно гладких функций, не имеющих разрывов в области р"аз-ложения, довольно точно воспроизводятся рядом Тейлора. Как правило, такие разложения достаточно просты в окрестностях узловой точки разложения.

Для разложения

в ряд используются следующие функции системы Mathematical

Series[f, {х, х0, п}]— выполняет разложение в степенной ряд функции f в окрестности точки х=х0 по степеням (х-х0) ^{^} n; Series [f, {х, х0, nх}, {у, у0, nу}] — последовательно ищет разложения в ряд сначала по переменной у, затем по х; SeriesCoef ficient [s,n] — возвращает коэффициент при переменной n-й степени ряда s; SeriesData [х, х0, {а0, al,...}, nmin, nmax, den] —представляет степенной ряд от переменной х в окрестности точки х0. Величины ai являются коэффициентами степенного ряда. Показатели степеней (х-х0) представлены величинами nmin/den, (nmin+1) /den, ..., nmax/den. Суть разложения функции в степенной ряд хорошо видна из разложения обобщенной функции/(д:), представленного на рис. 5.1 (выходные ячейки имеют стандартный формат).

Рис. 5.1. Разложение в ряд обобщенной функции f(x)

В первом примере разложение идет относительно исходной точки х0=0, что соответствует упрощенному ряду Тейлора, часто называемому рядом Маклорена. Во втором случае разложение идет относительно исходной точки х0, отличной от нуля. Обычно такое разложение сложнее и дает большую остаточную погрешность.

В соответствии с принятой математической символикой эта погрешность обозначается как О [x] ⁱ с показателем степени, указывающим на порядок погрешности. Следует отметить, что разложение в ряд использует особый формат вывода, частью которого и является член остаточной погрешности. На рис. 5.2 показано разложение в ряд Тейлора для нескольких функций, причем вывод дан в стандартной форме.

Рис. 5.2. Примеры представления функций рядами

Нетрудно заметить, что не все функции разлагаются в ряд Тейлора системой . Mathematica. Например, не имеют разложения логарифм и квадратный корень — они возвращаются в исходном виде. А разложение факториала представлено через гамма- и полигамма-функции.

Удаление члена с остаточной погрешностью ряда

Из-за особого формата результаты разложения в ряд нельзя явно использовать для расчетов (например, для построения графика функции по данным ее разложения в ряд). Для устранения остаточного члена и получения приемлемых для расчетов выражений можно использовать функции Collect и Normal. Ниже показаны примеры применения этих функций:

Series[Sin[x],{х,0,7}]
x-x3/6+x5/120 -x7/5040+0[Xl 8
Collect[%,x]
x-x3/6+x5/120 -x7/5040
Normal[Series[Sin[x*y],{х,0,3},{у,0,3}] ]
xy-х3 у3/6
f [х_, у ] =xy-х3 у3/6
xy-х3 у3/6
f[0.1,0.2]
0.0199987

В данном случае результат представлен в формате стандартного вывода. Его можно использовать для создания функций пользователя, например, путем переноса через буфер обмена в правую часть такой функции. Это и показано в конце приведенных выше примеров. Разумеется, можно задать функцию пользователя и напрямую:

F[x_, у_] = Normal [Series [Sin[x* у] , {х, 0, 3), {у, 0, 3}]
xy-х3 у3/6
F[0.1, 0.2]
0.0199987

В Mathematica 3/4 преобразование результатов разложения в ряд в стандартные расчетные выражения несколько упрощено. Это позволяет ограничиться описанными выше (но вовсе не единственными) приемами.

Графическая визуализация разложения в ряд

Погрешность разложения в ряд возрастает с ростом отклонения от узловой точки. При больших отклонениях даже качественное описание функции может резко нарушаться — например, монотонно возрастающая функция при вычислении по разложению в ряд может убывать или даже стремиться к бесконечности. Для оценки того, насколько и в какой окрестности исходной точки разложение в ряд адекватно разлагаемой функции, полезно построить на одном рисунке график исходной функции и график выражения, соответствующего полученному ряду (без остаточной погрешности). Другими словами, нужна графическая визуализация разложения в ряд.

Пример графической визуализации разложения в ряд представлен на рис. 5.3. На нем, кстати, использовано описанное выше применение функции Collect для получения результата разложения в обычной форме, допускающей вычисления.

Рис. 5.3. Представление синусоидальной функции рядом Тейлора с графической иллюстрацией его точности

На рис. 5.3 представлены график синусоиды, построенной по аналитическому выражению, и график ее разложения в ряд Тейлора в окрестности точки х ₀ =2. Хорошо заметно расхождение за пределами области, примыкающей к оперной точке функции. Как отмечалось, погрешность уменьшается, если х0=0 (ряд Маклорена). К сожалению, при большом числе членов ряда его поведение становится трудно предсказуемым, и погрешность приближения катастрофически нарастает.

Преобразования Фурье

Основные понятия о спектральном анализе и синтезе

Спектральный подход (метод) лежит в основе целых направлений науки и техники. Достаточно отметить, что он плодотворно используется в технике электро- и радиосвязи, где разделение частот модулированных сигналов базируется на различии их спектров. Спектральный подход также широко используется для создания аналоговых и цифровых фильтров и для оценивания искажений сигналов в ходе их преобразования, например усиления реальными усилителями.

Схема применения спектрального подхода достаточно проста. Сигнал вначале представляется совокупностью гармонических составляющих — гармоник ~ в виде тригонометрического ряда Фурье. Для точного представления сигнала требуется бесконечное число гармоник, но на практике оно всегда ограничено. Такое ограничение порождает волнообразный характер изменения сигнала и появление выбросов, что известно под названием эффекта Гиббса.

Получение сигнала в виде суммы гармонических составляющих получило название спектрального анализа. Суммирование гармоник сигнала и его приближенное представление во временной области называется гармоническим синтезом сигнала.

Итак, спектральный подход заключается в следующем. Вначале получают достаточно представительный (с большим числом гармоник) спектр заданного сигнала. Довольно часто используют тестовые сигналы в виде прямоугольных, треугольных, пилообразных и других импульсов. Для моделирования таких сигналов можно использовать различные функции, например, Sign [Sin [t] ] позволяет получить симметричные прямоугольные импульсы (меандр), а Abs [Sin [t] ] моделирует результат двухполупериодного выпрямления синусоидального напряжения. Для получения разрывных сигналов можно использовать функции с условиями сравнения, например функцию If (на рис. 5.4 даны примеры имитации с помощью этой функции импульсов прямоугольной и пилообразной формы).

Для многих частных видов сигналов (а к ним относится большинство тестовых сигналов) разложения в ряд Фурье хорошо известны и приводятся в любом математическом справочнике (иногда в несколько разных формах). Это позволяет сразу получить нужное число гармоник сигнала и, что особенно важно, проверить, насколько адекватно синтезируемый сигнал описывает реальный сигнал.

На рис. 5.5 показан пример прямого синтеза разнополярных коротких прямоугольных импульсов. Используется известное разложение их в ряд, причем графики построены для 5 и 20 гармоник. Нетрудно заметить, что даже при двадцати гармониках представление такого сигнала гармоническим рядом не очень точно — отчетливо наблюдаются колебания и выбросы, то есть эффект Гиббса.

Рис. 5.4. Имитация импульсов прямоугольной и пилообразной формы с помощью функции If

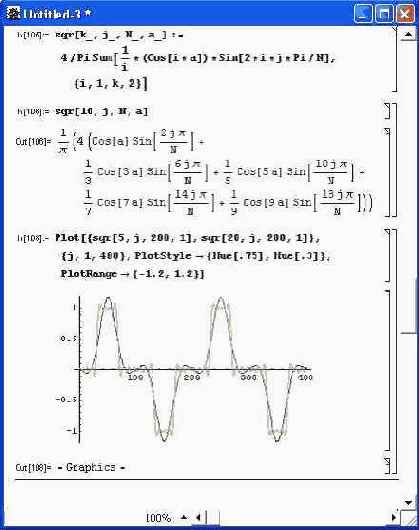
Рис. 5.5. Гармонический синтез коротких разнополярных прямоугольных импульсов

Еще один подобный пример — синтез разнополярных треугольных импульсов — представлен на рис. 5.6. Здесь также используется известное выражение для ряда

Фурье. Графики построены для 3 и 20 гармоник. Нетрудно заметить, что гармонический синтез для этого сигнала дает гораздо лучшие результаты — даже три гармоники неплохо воспроизводят сигнал. Это связано с тем, что данный сигнал не имеет разрывов — для него характерны лишь точки резких перегибов временной зависимости.

Рис. 5.6. Гармонический синтез симметричных треугольных импульсов

В целом надо отметить, что чем плавнее временная зависимость сигнала, тем меньше проявляются отмеченные выше искажения и слабее заметен эффект Гиббса.

Итак, в результате гармонического анализа сигнала (или его прямого гармонического синтеза) сигнал получается в виде совокупности гармонических сигналов — гармоник. В общем случае каждая гармоника имеет свою амплитуду и фазу, и для их получения в общем случае можно использовать прямое преобразование Фурье (см. ниже).

Полученный спектр сигнала можно подвергать различным преобразованиям, например частотной фильтрации. Полученный после этого измененный спектр гармоник используется (путем гармонического синтеза) для воссоздания искаженного (например, после фильтрации) сигнала.

Простота спектрального подхода обманчива, поскольку он требует довольно громоздких вычислений. Для быстрого их выполнения были созданы различные ускоренные методы спектрального анализа и синтеза — например, метод быстрого преобразования Фурье (БПФ). Но лишь с появлением СКМ класса Mathematica (и ей подобных) спектральный подход превращается в «рабочую лошадку», обеспечивая наглядное и достаточно быстрое решение задач спектрального анализа и синтеза.

Прямое и обратное преобразования Фурье

Для представления временных зависимостей (сигналов) в виде набора гармоник в общем случае (и в системе Mathematica) используется прямое дискретное преобразование Фурье (ДПФ), а для обратного преобразования спектра во временную зависимость — обратное дискретное преобразование Фурье. Математические основы этих преобразований хорошо известны и описаны в соответствующей литературе. В Mathematica 4 имеются следующие основные функции для осуществления дискретного преобразования Фурье:

Fourier [list] — осуществляет дискретное преобразование Фурье для списка list комплексных чисел; InverseFourier [list] — осуществляет дискретное обратное преобразование Фурье списка list комплексных чисел. Параметром list этих функций в общем случае является список, содержащий комплексные числа. Последовательное применение прямого и обратного преобразований Фурье должно приводить к результату, совпадающему с исходными данными (в пределах малой погрешности). Это хорошо подтверждает следующий пример:

DF:=Fourier[{1,1,0,0}]
DF
{1. + 0.I, 0.5+0.51, 0. + 0.I, 0.5-0.51}
IF:=InverseFourier[DF]
IF
{1.+ 0. I, 1. + 2.77556х10-171, 0. + 0. I, 0. -2.77556x 10-17I}

Разумеется, этот пример носит исключительно тестовый характер. Используя множество возможностей работы с комплексными числами, можно решать различные задачи спектрального анализа и синтеза сигналов различной формы.

Применение описанных функций имеет некоторые тонкости. Прежде всего надо отметить, что отсчет элементов векторов начинается не с нуля, а с единицы. Поэтому нулевая гармоника (в электро- и радиотехнике ее называют постоянной составляющей разлагаемой в ряд Фурье зависимости) соответствует индексу 1, первая гармоника — индексу 2 и т. д. Таким образом, имеет место смещение нумерации индексов на единицу.

Согласно теореме отсчетов, именуемой также теоремой Котельникова, если функция имеет N отсчетов, то максимальное число гармоник спектрального разложения равно N/2. Между тем, функция Fourier в системе Mathematica дает все N элементов создаваемого ею вектора. При этом на спектрограмме «лишние» гармоники на деле просто образуют зеркальное отображение реально возможных N/2 гармоник. Именно поэтому двойное (прямое и обратное) преобразование Фурье в системе Mathematica 3/4 почти идеально точно восстанавливает исходный вектор.

Еще одна тонкость связана с необычным представлением нулевых мнимых частей элементов векторов, получаемых в ходе преобразований. Они записываются в виде 0.1. Для их устранения может использоваться функция Chop [V].

Для лучшего понимания особенностей спектрального анализа и синтеза рекоменду.ется внимательно ознакомиться с формулами преобразований Фурье, которые можно найти в справочной системе, благо эти формулы вполне понятны даже тем, кто не силен в английском языке. В литературе подобные формулы встречаются в нескольких различных видах, что порождает некоторые трудности в интерпретации и нормировке результатов спектрального анализа и синтеза. Поэтому полезно познакомиться с дополнительными и вполне конкретными примерами, приведенным ниже.

Спектральный анализ на основе прямого преобразования Фурье

Итак, прямое преобразование Фурье означает перевод временного представления сигнала в частотное. Другими словами, оно позволяет получить частотный спектр сигнала, представленного отсчетами его временной зависимости. Нередко это является конечной целью спектрального анализа.

На рис. 5.7 представлен пример спектрального анализа простого сигнала — треугольного импульса, заданного с помощью функции If. Затем с помощью функции Fourier прямого преобразования Фурье получены в явном виде векторы амплитуд Мg и фаз Аg гармоник этого сигнала.

Рис. 5.7. Спектральный анализ пилообразного импульса на основе прямого преобразования Фурье

На рис. 5.8 представлено продолжение документа, показанного на рис. 5.7. Здесь с помощью графиков лестничного типа, подчеркивающих дискретность гармоник, построены спектрограммы амплитуд и фаз гармоник пилообразного импульса. Хорошо видно симметричное отражение линий спектра относительно восьмой гармоники — в нашем случае имелось 16 отсчетов сигнала. Это значит, что амплитуда и фаза девятой гармоники те же, что у седьмой гармоники, у десятой — те же, что у шестой, и т. д.

Рис. 5.8. Спектрограммы амплитуд и фаз гармоник пилообразного импульса

Теперь рассмотрим более сложный случай — получение спектра сложного сигнала (рис. 5.9). :

Рис. 5.9. Получение спектра сложного сигнала с помощью прямого преобразования Фурье

В начале этого рисунка показано формирование синусоидального сигнала с частотой 50 Гц, на который наложена значительная по амплитуде шумовая составляющая. Она создается добавлением к отсчетам сигнала случайных величин, созданных генератором случайных чисел.

Во второй части рисунка показан график частотных отсчетов, полученных после прямого преобразования Фурье. На нем отчетливо виден пик в районе частоты 50 Гц (поскольку первый элемент результирующего списка соответствует нулевой частоте, этот пик возникает на 51-м элементе списка). Однако помимо него существует еще один пик на частоте 256 - 50 = 206 Гц. Он связан с отмеченным ранее свойством симметрии спектра вещественного сигнала.

Фильтрация сигналов на основе преобразований Фурье

Преобразование Фурье является теоретической основой фильтрации сложных сигналов. Мы рассмотрим комплексный пример на фильтрацию сигнала, представляющего собой функцию Бесселя первого рода третьего порядка. Рисунок 5.10 показывает верхнюю часть документа, демонстрирующую создание исходного сигнала и описание частотного фильтра.

Рис. 5.10. Часть документа, показывающая создание сигнала и синтез фильтра для него

Как и в ранее рассмотренном примере, сигнал формируется как сумма чистого сигнала со случайной составляющей, моделирующей шум. Выбранная форма сигнала напоминает затухающую синусоиду. Уровень шумов выбран достаточно большим, так что форма чистого сигнала с трудом угадывается на фоне шумов (верхний график). Далее показаны синтез цифрового частотного фильтра и его амплитудно-частотная характеристика (АЧХ). График АЧХ показан в нижней части рис. 5.10.

На рис. 5.11 показан процесс фильтрации. Он сводится к уточнению модели фильтра (сдвигу АЧХ в область более низких частот и созданию зеркального отражения спектра), проведению прямого преобразования Фурье, выделению фильтром соответствующих составляющих сигнала и, наконец, выполнению обратного преобразования Фурье. Оба преобразования и фильтрация осуществляются в одном выражении (строка с переменной conv). При этом векторы прямых преобразований Фурье для сигнала и для отсчетов частотной характеристики фильтра перемножаются. Обратное преобразование Фурье переводит результат фильтрации во временную область. Полученный в результате фильтрации сигнал практически очищен от шума. Это подтверждает график выходного сигнала, представленный в нижней части рис. 5.11.

Рис. 5.11. Часть документа, показывающего фильтрацию сигнала и построение графика сигнала, очищенного от шума

Эти примеры показывают высокую эффективность средств Mathematica 3/4 в решении задач спектрального анализа, синтеза сигналов, их фильтрации и иных преобразований. Важно отметить, что в новейшей версии Mathematica 4 использованы ускоренные алгоритмы преобразований Фурье, повышающие скорость выполнения описанных операций в несколько раз. Это открывает возможность решения серьезных задач обработки сигналов, представленных многими тысячами отсчетов. Другими словами — сигналов, реально применяемых в технике связи.

Функции пакета — FourierTransform

Подпакет FourierTransform пакета Calculus в версии Mathematics 3 служит для осуществления расширенных преобразований Фурье. Он вызывается командой

<<Calculus` FourierTransform`

Ввиду важности этих преобразований в системе Mathematica 4 их функции были размещены уже в ядре системы. Это следующие функции:

FourierTransform [expr, t, w] — возвращает результат прямого преобразования Фурье над выражением expr [t], выраженного через переменную w; InverseFourierTransform[expr, w, t] — возвращает результат обратного преобразования Фурье над выражением expr[w], выраженного через переменную t; FourierCosTransform[expr, t, w] — возвращает результат косинусного преобразования Фурье над выражением expr [t ], выраженного через переменную w; FourierSinTransform[expr, t, w] — возвращает результат синусного преобразования Фурье над выражением expr [t], выраженного через переменную w; FourierTransform [expr, {tl,t2}, {wl, w2 } ] — возвращает результат прямого преобразования Фурье над выражением expr [ tl, t2,...], выраженного через переменные {wl, w2,-...}; InverseFourierTransformtexpr, {tl,t2}, {wl,w2} ]'— возвращает результат обратного преобразования Фурье над выражением expr [ wl, wl,...], выраженного через переменные {tl, t2,...}., Примеры осуществления прямого и обратного преобразований Фурье представлены ниже:

FourierTransform[Sin[t]*t:2, t, w]
-Iл(DiracDelta"[l - w] - DiracDelta" [1 + w])
InverseFourierTransform[%, w, t]
t2Sin[t]
FourierCosTransform[Sin[t]*t:2, t, w]
-8w2/(1-w2)3-2/(1-w2)2
FourierSinTransform[Cos[a*t], t, w]
-w/(a2-w2)
FourierTransform[tl^2 Exp[-a t2] UnitStep[tl, t2],
{tl, t2}, {wl, w2}]
-2I/w13-лDiracDelta''[w1]/a-IW2
InverseFourierTransformtwl/(l-b*w2), {wl, w2}, {tl, t2}]

Для реализации спектрального анализа и синтеза имеются следующие функции:

FourierExpSeries [expr, {x, xmin, xmax), n] — возвращает разложение expr [х] в экспоненциальный ряд Фурье с n членами на отрезке {xmin, xmax}; FourierExpSeriesCoef f icient [expr, {x, xmin, xmax} ,n] —возвращает коэффициенты разложения expr [x] в экспоненциальный ряд Фурье с n членами на отрезке {xmin, xmax}; FourierTrigSeries [expr, {x, xmin, xmax}, n] — возвращает разложение expr [x] в тригонометрический ряд Фурье с n членами на отрезке {xmin, xmax}; FourierSinSeriesCoef f icient [expr, {x, xmin, xmax}, n] —возвращает синусные коэффициенты разложения expr [x] в тригонометрический ряд Фурье с n членами на отрезке {xmin,xmax}; FourierCosSeriesCoef f icient [expr, {x, xmin, xmax}, n] —возвращает косинусные коэффициенты разложения expr [x] в тригонометрический ряд Фурье с n членами на отрезке {xmin, xmax}. Рисунок 5.12 иллюстрирует создание пилообразного сигнала, его разложение в тригонометрический ряд Фурье с п = 4, графическое воспроизведение сигнала и его представление суммой из четырех гармоник (на рисунке оставлены только совмещенные графики). Таким образом, последняя операция демонстрирует проведение синтеза пилообразного сигнала по четырем гармоникам.

Рис. 5.12. Создание пилообразного сигнала, его разложение в тригонометрический ряд Фурье и синтез сигнала по четырем гармоникам

Помимо указанных функций существует целая группа функций для численных операций, связанных с разложением в ряд Фурье. Все они имеют в начале имени букву N, например:

NFourierTrigSeries [expr, {x, xmin,xmax}, n] — возвращает разложение expr t x ] в тригонометрический ряд Фурье с n членами на отрезке {xmin, xmax} в численном виде. Предоставляем читателю опробовать эти функции самостоятельно.

Интерполяция, аппроксимация и регрессия

Нередко исходные данные при решении математических задач представлены рядом точек произвольной зависимости вида у(х). Сама по себе эта зависимость может быть неизвестной. Для вычисления промежуточных значений функции используется аппарат интерполяции. При нем истинная функция заменяется аппроксимирующей функцией, которая в узловых точках дает точные значения ординат и позволяет вычислить значения интерполируемой функции в промежуточных точках.

Полиномиальная интерполяция и аппроксимация

Для решения задач интерполяции и аппроксимации функций, заданных рядом узловых точек, в Mathematica используются следующие функции:

InterpolatingFunctionfrange, table] — возвращает интерполирующую функцию, позволяющую вычислять промежуточные значения в заданном диапазоне range для таблицы table; InterpolatingPolynomial [data, var] — возвращает полином (степенной многочлен) по переменной var, значения которого в узловых точках точно совпадают с данными из списка data. Он может иметь форму { {xl, f1}, {х2, f2},...} или {fl, f2,...} (во втором случае xi принимают значения 1, 2,...). Вместо fi может быть список {fi, dfi, ddfi,...}, указывающий значения производных в точках xi; Interpolation [data] — конструирует объект InterpolatingFunction. InterpolationOrder — опция функции Interpolation, указывающая степень подходящего полинома. При ее значении, равном 1, осуществляется кусочно-линейная интерполяция. Целое значение, большее единицы, задает степень глобальной полиномиальной интерполяции.

Применение основной функции Interpolation поясняет следующий пример:

data = ТаЫе[{х, х^2 + 1}, {х, 1, 5}]
{{1, 2}, {2, 5}, {3, 10}, {4, 17}, {5, 26}}
funi = Interpolation[data]
InterpolatingFunctionf{{1, 5}}, 0]
{funi [1.5], funi[3], funi[4.5]}
{3.25, 10, 21.25}

Таким образом, на заданном отрезке изменения х функция Interpolation позволяет найти любое промежуточное значение функции funi [x], в том числе значения в узловых точках.

Теперь рассмотрим часто используемую полиномиальную аппроксимацию, при которой ищется полином, график которого точно проходит через узловые точки данных.

Степень интерполирующего (и аппроксимирующего) полинома всегда на 1 меньше числа узловых точек интерполяции или аппроксимации. Аппроксимация отличается от интерполяции тем, что предполагает получение аппроксимирующей функции в явном виде. При полиномиальной аппроксимации такой функцией является степенной многочлен.

Пример на рис. 5.13 иллюстрирует технику проведения полиномиальной аппроксимации с применением интерполирующего степенного многочлена.

Рис. 5.13. Полиномиальная аппроксимация таблично заданных данных

Как и следовало ожидать, степень аппроксимирующего многочлена оказалась равной трем, поскольку было задано четыре пары данных. На рис. 5.13 представлено также сравнение результата полиномиальной аппроксимации с исходными данными. Исходные данные представлены на графике в виде точек, а зависимость, представленная аппроксимирующим полиномом, выведена сплошной линией.

В узлах интерполяции значения интерполирующего многочлена точно совпадают со значениями исходных данных. Однако это не гарантирует малую погрешность за пределами узловых точек (особенно при экстраполяции функций). Чем больше пар данных и чем выше степень аппроксимирующего многочлена, тем выше погрешность аппроксимации. Обычно аппроксимация при степени многочлена выше 8-10 не применяется из-за резкого возрастания погрешности. При большом числе пар исходных данных более полезной на практике является регрессия.

Регрессия и визуализация ее результатов

Еще один широко используемый вид аппроксимации — регрессия. Она заключается в нахождении параметров некоторой функции регрессии, при которой график этой функции проходит в «облаке» узловых точек, обеспечивая наименьшую среднеквадратичную погрешность их представления. В отличие от интерполяции, при регрессии найденная функция не дает точного значения ординат в узловых точках — она просто минимизирует погрешность вычислений в этих точках.

Для решения задач регрессии используется функция ядра

Fit: Fit[data, funs, vars]

Эта функция ищет приближение для списка данных data методом наименьших квадратов в виде линейной комбинации функций funs переменных vars. Данные data могут иметь форму {{xl, yl,..., f1}, {х2, у2,..., f2 },...}, где число координат х, у,... равно числу переменных в списке vars. Также данные data могут быть представлены в форме {f 1, f 2, =..} с одной координатой, принимающей значения 1, 2... Аргумент funs может быть любым списком функций, которые зависят только от объектов vars.

Следующие примеры показывают приближение исходных данных степенным полиномом и линейной комбинацией двух функций:

Fit[{{0, 0.9}, {2, 8.099999999999999), {3, 17}, {4, 33}}, {а, х, х2}, х]
0. 997273-1.40864 х+2.33409 х2
Fit[{{0, 0.9}, {2, 8.099999999999999}, {3, 17}}, {х2, Ехр[х], х} , х]
0.9ех + 2.89276х- 1.08392 х2

Здесь в первом примере выполняется полиномиальная регрессия со степенью полинома, равной 2. Максимальная степень на 1 меньше числа пар исходной зависимости (в нашем случае их 4) — при такой степени регрессия вырождается в обычную полиномиальную аппроксимацию, которая рассматривалась ранее.

Рисунок 5.14 показывает несколько иной путь проведения полиномиальной аппроксимации — исходные данные заданы объектом-списком data.

В конце документа рис. 5.14 показано построение графика аппроксимирующего полинома второй степени и точек исходных данных. Заметно, что при регрессии график полинома проходит в середине «облака» исходных точек и не укладывается на них точно.

В уроке 12 будут рассмотрены дополнительные функции для проведения регрессии. Они входят в различные пакеты расширения системы Mathematica 3/4.

Рис. 5.14. Полиномиальная регрессия с графическим выводом

Спектральный анализ с линейной интерполяцией сигнала

Как уже отмечалось, одной из проблем точного представления сигналов при гармоническом синтезе является ограничение числа гармоник, связанное с конечностью числа отсчетов сигнала. К примеру, если вещественный сигнал задан 20 отсчетами, то максимальное число гармоник будет всего 10, что недостаточно для хорошего представления большинства реальных сигналов.

Ниже описан путь преодоления этого ограничения. Он основан на интерполяции сигнала, что позволяет при ограниченном числе его отсчетов (выборок) использовать любое число дополнительных отсчетов. Разумеется, при этом строится спектр интерполированного сигнала, но он может представлять реальный сигнал гораздо лучше, чем просто ограниченный N/2 гармониками спектр сигнала с малым числом выборок.

Еще одна проблема при спектральном анализе связана с необходимостью нормировки коэффициентов Фурье. Их расчет по аналитическим формулам не является достаточно эффективным — уже давно доказано, что если сигнал представлен отдельными выборками, то единственно обоснованным методом вычисления интегралов (коэффициентов) Фурье является простейший метод прямоугольников. Это обстоятельство также учтено в описанном ниже документе (вполне законченном «блокноте» системы Mathematica).

Пусть сигнал задан N отсчетами. На рис. 5.15 показан пример задания достаточно сложного сигнала путем формирования вектора его ординат Yi (индекс i от 1 до 20). Пусть сигнал задан на периоде Т = 4*10^-6 с, что соответствует частоте f 1 основной гармоники сигнала, равной 250 кГц. Рисунок 5.15 поясняет технику нормировки сигнала и построения его графика с реальной шкалой времени (то есть на отрезке времени от 0 до Т).

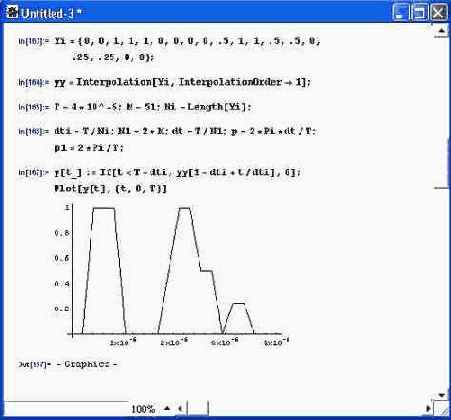
Рис. 5.15. Задание сигнала, его кусочно-линейная интерполяция и построение графика временной зависимости

При построении графика сигнала и его временной зависимости использована наиболее широко применяемая на практике техника кусочно-линейной интерполяции. Однако изменением значения опции InterpolationOrder можно выполнить и глобальную полиномиальную аппроксимацию сигнала, которая может быть предпочтительна для гладких сигналов.

Рисунок 5.16 показывает раздел документа с расчетом коэффициентов косинусных и синусных коэффициентов Фурье методом прямоугольников. В расчете есть небольшая тонкость, иногда ускоряющая вычисления, — нулевые отсчеты не обрабатываются. Показанные на рис. 5.16 соотношения хорошо знакомы специалистам, применяющим инженерные методы спектрального анализа и синтеза.

На рис. 5.17 крупным планом показано построение спектрограммы амплитуд гармоник заданного сигнала. Дабы подчеркнуть дискретность гармоник, амплитуда каждой из них показана точкой, около которой стоит номер гармоники. Для этого пришлось использовать графическую функцию LabelListPlot из пакета расширения Graphics. Нетрудно заметить, что амплитуды гармоник быстро убывают по мере роста их номера. Однако, поскольку суммируется множество гармоник, это не является основанием для слишком поспешного отбрасывания высших гармоник.

Рис. 5.16. Вычисление коэффициентов Фурье, амплитуд и фаз гармоник

Рис. 5.17. Спектрограмма амплитуд гармоник

Рисунок 5.18 представляет спектрограмму фаз гармоник. Фазы гармоник также имеют дискретные значения и показаны точками с номерами. Значение фазового сдвига лежит в пределах от -л до л.

Теперь, получив набор гармоник заданного сигнала, можно приступить к его гapмоническому синтезу. Он представлен на рис. 5.19 сверху. Здесь также применен прием, иногда ускоряющий вычисления, — гармоники с нулевой амплитудой из формулы синтеза устраняются.

Рис. 5.18. Спектрограмма фаз гармоник

Рис. 5.19. Гармонический синтез сигнала и сравнение его результатов с временной зависимостью интерполированного сигнала

Самый «волнующий» момент представлен во второй части рис. 5.19 — здесь показано сравнение результата гармонического синтеза сигнала с его временной зависимостью (интерполированной). Чтобы исходный и синтезированный сигналы не сливались, синтезированный сигнал намеренно немного сдвинут вправо и вверх. Нетрудно заметить, что несмотря на сложный характер сигнала его гармонический (спектральный) синтез в данном случае дает превосходные результаты уже при использовании 51 гармоники (включая нулевую). Если убрать отмеченный выше сдвиг, то сигналы практически сливаются.

Учет искажений сигнала

Рисунок 5.20 показывает задание амплитудно-частотной и фазо-частотной (ФЧХ) характеристик некоего фильтра, ослабляющего высокие частоты и вносящего фазовый сдвиг, пропорциональный частоте сигнала. В нижней части рисунка построены эти характеристики. Заметим, что здесь АЧХ и ФЧХ заданы без «хитростей», присущих решению аналогичной задачи с применением встроенных функций дискретного преобразования Фурье. Они задаются в явном виде как функции от частоты.

Рис. 5.20. Амплитудно-частотная и фазочастотная характеристики фильтра

Рисунок 5.21 показывает, как влияет на форму сигнала его прохождение через фильтрующую цепь. Для оценки этого используется формула синтеза гармоник. Однако отличные от нуля амплитуды гармоник умножаются на модуль коэффициента передачи (АЧХ) фильтра, а к фазе каждой гармоники добавляется фазовый сдвиг, вносимый фильтром (ФЧХ). Таким образом, в процессе синтеза временной зависимости сигнала учитываются амплитудно-частотные и фазо-частотные искажения сигнала фильтром.

Рис. 5.21. Сравнение исходной временной зависимости сигнала и сигнала на выходе фильтрующей цепи

Рассмотренный документ является хорошей иллюстрацией применения системы Mathematica для решения нестандартных задач и реализации альтернативных методов их решения. В частности, в данном случае спектральный анализ и синтез велись по типичной для инженерных расчетов методике и без использования встроенных функций преобразования Фурье.

Моделирование нелинейных цепей с применением интерполяции

Интерполяция может быть очень полезной при решении задач моделирования нелинейных цепей как с обычными (например, электронные лампы и транзисторы), так и с «необычными» активными приборами, например туннельными диодами или лавинными транзисторами.

Одна из проблем такого моделирования — задание нелинейных вольт-амперных характеристик (ВАХ) активного прибора. Mathematica позволяет задать такие ВАХ, используя различные виды интерполяции и аппроксимации — от кусочно-линейной до полиномиальной или сплайновой. Рисунок 5.22 демонстрирует простое табличное задание N-образной ВАХ туннельного диода с полиномиальной интерполяцией (используется полином четвертой степени). Обратите внимание на применение импортируемого рисунка — схемы цепи. Он готовился отдельно в графическом редакторе.

Рис. 5.22. Начало документа, позволяющего моделировать схему на туннельном диоде

Рисунок 5.23 показывает часть документа, в которой выполнено математическое моделирование поведения схемы с момента ее включения. Для моделирования используется известная система из двух нелинейных дифференциальных уравнений, решаемая с помощью встроенной функции NDSolve (эта система записана первой в списке параметров данной функции). Полученные в результате моделирования временные зависимости напряжения на туннельном диоде и тока во внешней цепи показаны ниже. Они свидетельствуют о возникновении в цепи стационарных и почти синусоидальных колебаний. Таким образом, цепь выполняет функции генератора высокочастотных колебаний

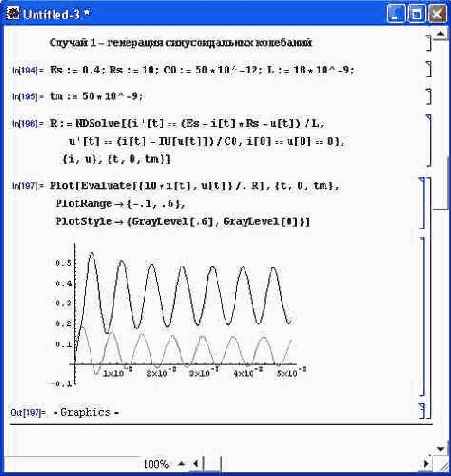
Рис. 5.23. Моделирование возникновения и установления синусоидальных колебаний в схеме на туннельном диоде

Поведение схемы очень наглядно характеризует фазовый портрет колебаний, представленный на рис. 5.24 и построенный на фоне интерполированной ВАХ туннельного диода и линии нагрузки резистора Rs, задающей положение рабочей точки на падающем участке ВАХ. В этом случае туннельный диод вносит во внешнюю цепь отрицательную дифференциальную проводимость, что и ведет к возможности возникновения гармонических или релаксационных колебаний (уменьшив С или увеличив L, вы можете посмотреть, как происходит переход к релаксационным колебаниям).

Рис. 5.24. Фазовый портрет колебаний в схеме с туннельным диодом для случая почти гармонических колебаний

Если задать вместо постоянного напряжения Es некоторый импульсный сигнал, то можно смоделировать множество других режимов работы цепи, например генерацию ждущих колебаний, нелинейное усиление, триггерный режим и т. д. Рисунок 5.25 показывает задание e(t) в виде постоянного напряжения Es, на которое наложены положительный и отрицательный запускающие импульсы.

Если линия нагрузки резистора Rs пересекает ВАХ туннельного диода в трех точках (две из них расположены на восходящих участках ВАХ), то будет наблюдаться триггерный режим с раздельным запуском. Этот случай показан на рис. 5.26, где построены временные зависимости напряжения и тока в триггере на туннельном диоде.

Риc. 5.25. Задание временной зависимости e(t), обеспечивающей триггерный режим работы схемы с туннельным диодом

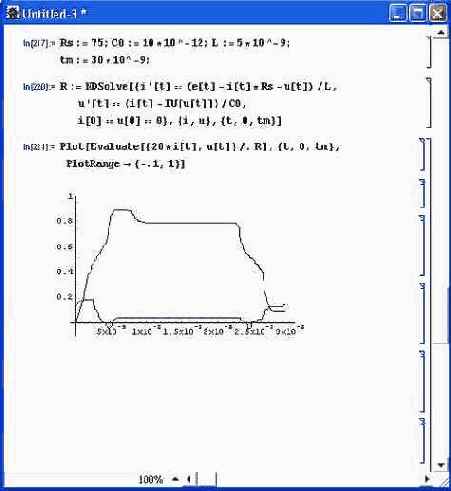
Риc. 5.26. Моделирование триггерного режима работы схемы с туннельным диодом

Фазовый портрет колебаний для этого случая представлен на рис. 5.27. Он дает хорошее представление о сложности физических процессов даже в такой, казалось бы, простой схеме, которая представлена на рис. 5.22.

Риc. 5.27. Фазовый портрет, иллюстрирующий работу схемы с туннельным диодом в триггерном режиме

Если собрать приведенные на рис. 5.22-5.27 фрагменты воедино, вы получите еще один полностью завершенный «блокнот», прекрасно иллюстрирующий решение одной из реальных научно-технических задач. Вы можете дополнить его анализом ряда других режимов работы схемы, причем не обязательно на туннельном диоде, а на любом приборе с нелинейной В АХ вида I(U). Для этого достаточно просто сменить вектор с табличными данными опорных точек ВАХ, полученных, например, в эксперименте, и использовать иные параметры схемы.

Что нового мы узнали

В этом уроке мы научились:

Находить разложения заданных функций и выражений в ряды Тейлора и Маклорена. Удалять член с остаточной погрешностью ряда. Представлять разложение в ряд графически. Осуществлять прямое и обратное дискретные преобразования Фурье. Выполнять спектральный анализ на основе преобразования Фурье. Осуществлять фильтрацию сигналов на основе преобразования Фурье. Выполнять полиномиальную интерполяцию и аппроксимацию. Осуществлять регрессию и визуализацию ее результатов. Выполнять спектральный анализ таблично заданных сложных сигналов с интерполяцией их временных зависимостей. Выполнять моделирование схем на приборах с N-образными ВАХ, используя при этом их интерполяцию.