Ортогональные многочлены

Одними из широко распространенных специальных функций являются ортогональные многочлены (полиномы). Mathematica имеет следующие функции, возвращающие значения ортогональных многочленов:

ChebyshevT [n, х] — полином Чебышева п-й степени первого рода; CyebyshevU [n, x] — полином Чебышева п-йстепени второго рода; HermiteH[n, х] — полином Эрмита

п-йстепени; JacobiP[n, a, b, х] — полином Якоби п-й степени; 'GegenbauerC [n, m, х] — полином Гегенбауэра; LaguerreL[n, х] — полином Лагерра n-й степени; LaguerreL[n, а, х] — обобщенный полином Лагерра п-й степени; LegendreP [n, х] — полином Лежандра n-й степени; LegendreP [n, m, x] — присоединенный полином Лежандра; LegendreQ [n, z] — функция Лежандра второго рода n-го порядка; LegendreQ [n, m, z] — присоединенная функция Лежандра второго рода. LegendreType — опция для функций LegendreP и LegendreQ; она указывает выборы разрывов кривой для функций Лежандра на комплексной плоскости.

Все ортогональные полиномы имеют простые рекуррентные представления. Поэтому приведенные выше функции вычисляются по ним довольно быстро и точно. Они находят широкое применение в технике интерполяции и аппроксимации функций.

Следующие примеры иллюстрируют работу с ортогональными многочленами.

Ввод (In)	Вывод (Out)
ChebyshevT [ 8, х]	1 - 32 x 2 + 160 x 4 - 256 x 6 + 128 x 8
ChebyshevT [5, 0.2]	0.84512
ChebyshevU [3,0. 15]	-0.573
HermiteH[4,3]	876
JacobiP[3,l,2,0.2]	-0.256
GegenbauerC [ 3 , 1 , x]	-4 x + 8 x 3
N [LaguerreL [3,x]]	0.166667 (6. -18. x+ 9. x 2 - 1. X 3 )
LegendreP [ 5 , x ]	15 x /6-35 x 3 /4+63 x 5 /8
LegendreQ[2,0.2]	-0.389202

Важно отметить, что при указании конкретного значения параметра п и символьном значении параметра х функции этой группы возвращают присущие им представления через степенные многочлены с соответствующими коэффициентами.

На рис. 6.1 показаны графики ортогональных полиномов Чебышева ChebyshevT и ChebyshevU. Для этих полиномов характерно изменение от -1 до +1 при \х\<1, причем при высоком порядке полиномов графики функций имеют колебательный характер.

Рис. 6.1. Графики ортогональных полиномов Чебышева ChebyshevT (сверху) и ChebyshevU (снизу)

Графики функций полиномов Лагерра LaguerreL и Лежандра LegendreP показаны на рис. 6.2. Они дают представление о поведении этих функций.

Рис. 6.2. Графики ортогональных полиномов Лагерра LaguerreL и Лежандра LegendreP (снизу)

На рис. 6.3 представлены графики полиномов Лежандра LegendreQ.

Рис. 6.3. Графики функций Лежандра LegendreQ (сверху) и полиномов Гегенбауэра GegenbauerC (снизу)

 

Интегральные показательные и родственные им функции

К другой известной группе специальных функций относятся интегральные показательные и родственные им функции:

Coshlntegralfx] — гиперболический интегральный косинус; Coslntegral [х] — интегральный косинус С1(х); Erf [z] — функция ошибок (интеграл вероятности); Erf[z0, zl] — обобщенная функция ошибок erf (zl)-erf (z0); Erf с [z] — дополняющая функция ошибок 1-erf (z); Erfi [z] — мнимое значение функции ошибок erf (iz) /i; ExplntegralE [n, z] — интегральная показательная функция Е(п,z); ExplntegralEi[z] — интегральная показательная функция Ei(z); Loglntegral [z] — интегральный логарифм li(z); Sinhlntegral [x] — интегральный гиперболический синус; Sinlntegral [х] — интегральный синус 81(лг). Ниже представлены примеры применения этих функций.

На рис. 6.4 представлены графики ряда интегральных показательных функций, дающие представление об их поведении при вещественном аргументе.

Следует обратить внимание на то, что большая часть этих функций может иметь комплексный аргумент. Для получения численных значений функций нужно задавать аргумент в форме вещественного числа или ¹ комплексного числа с вещественными действительной и мнимой частями.

Рис. 6.4. Графики интегральных показательных функций

 

Гамма- и полигамма-функции

Широко используются гамма-функция и относящиеся к ней родственные функции:

Gamma [ а ] — эйлерова гамма-функция; Gamma [ a, z] — неполная гамма-функция; Gamma [a, z 0, z 1 ] — обобщенная неполная гамма-функция Gamma (а, z 0) -Gamma(a,zl); GammaRegularized[a, z] — регуляризованная неполная гамма-функция (а,2)=Gamma(а,z)/Gamma(a); GammaRegularized[a, z0, zl] — обобщенная неполная гамма-функция Q(a,z0)-Q(a, zl); LogGamma [ z ] — логарифм эйлеровой гамма-функции; Pol у Gamma [ z ] — дигамма-функция \|/(z); Pol у Gamma [n, z] — n-я производная от дигамма-функции. Приведем примеры вычисления этих функций.

Как видно из этих примеров, данный класс функций (как и многие другие) определен в общем случае для комплексного значения аргумента.

На рис. 6.5 представлены графики эйлеровой гамма-функции и неполной гамма-функции при вещественном аргументе. Поведение эйлеровой гамма-функции довольно сложно, особенно при отрицательных значениях аргумента — наблюдаются характерные разрывы функции с ее уходом в положительную и отрицательную бесконечность.

Рис. 6.5. Графики эйлеровой гамма-функции (сверху) и неполной гамма-функции (снизу)

Поведение эйлеровой гамма-функции в комплексной плоскости довольно интересно. На рис. 6.6 показан контурный график этой функции, отражающий ее поведение на комплексной плоскости в ограниченной области изменения действительной и мнимой частей аргумента.

Рис. 6.6. Контурный график эйлеровой гамма-функции на комплексной плоскости

Графики других гамма-функций пользователь может' построить и просмотреть самостоятельно.

 

Функции Бесселя

 

Функции Бесселя, являющиеся решениями линейных дифференциальных уравнений вида z ² y" + zy'+ (z ² - п ² )у = 0, широко используются в анализе и моделировании волновых процессов. В системе Mathematica к этому классу относятся следующие функции:

Bessell[n, z] — модифицированная функция Бесселя первого рода I(n, z); BesselJ[n, z] — функция Бесселя первого рода J(и, z); BesselK[n, z] — модифицированная функция Бесселя второго рода К(п, z); BesselY[n, z] — функция Бесселя второго рода Y(n, z). Соотношения между этими функциями хорошо известны. Следующие примеры показывают вычисление функций Бесселя.

Ввод (In)	Вывод (Out)
Bessell[0,l.]	1.26607
Bessell[3,l.]	0.0221684
Bessell[l,2.+3.*I]	-1.26098 + 0.780149 I
Bessell[2,2.+3.*I]	1.25767 + 2.31877 I
BesselK[2,2.+3.*I]	-0.0915555 + 0.0798916 I
BesselY[2,2.+3.*I]	-2.3443 + 1.27581 I
BesselY[2,2.+3.*I]
N[BesselJ[l,0.5]]	0.242268
N[BesselJ[l, 2+1*3]]	3.78068- 0.812781 I

Приведем также пример на вычисление производной от функции Бесселя:

D[BesselJ[l, x], (х, 2}]

1/2 (-BesselJ[l, x] +

1/2 (-BesselJ[l, x] +BesselJ[3, x]) )

Нетрудно заметить, что результат в данном случае также представлен через функции Бесселя.

В другом примере — вычислении интеграла от функции Бесселя — результат выражается через гипергеометрическую функцию:

Integrate[BesselJ[2,x],x]

1/24 x3 HypergeometricPFQ [ { 2/3 }, { 5/2,3}, -x2/4]

На рис. 6.7 показаны графики функций Бесселя Bessell и BesselJ первых четырех порядков.

Рис. 6.7. Графики функций Бесселя Bessell (сверху) и Bessell (снизу) первых четырех порядков

Графики других функций Бесселя вы можете получить самостоятельно. Они представляют меньший интерес, чем графики, приведенные на рис. 6.7.

 

Гипергеометрические функции

Класс гипергеометрических функций в системе Mathematica представлен следующими встроенными в ядро функциями:

HypergeometricU [a, b, z] — конфлюэнтная (вырожденная) гипергеометрическая функция U(a, b, z); Hypergeometric0Fl [a, z] — гипергеометрическая функция ₀ F ₁ , (; a; z); HypergeometriclFl [а, b, z] — вырожденная гипергеометрическая функция Куммера ₂ F ₁ (a; b; z); Hypergeometric2Fl [a, b, с, z] — гипергеометрическая функция F ₁ (a, b; c, z). Следующие примеры показывают вычисления гипергеометрических функций.

Ввод (In)	Вывод (Out)
HypergeometricOFl [2 . , 1 . ]	1.59064
HypergeometricOFl [2 . , 2 . +3 . *I]	1.22457 + 2.31372 I
HypergeometriclFl [1 . , 2 . , 2 . +3 . *I]	-1.03861 + 2.07929 I
Hypergeometric2Fl[l. ,2. ,3. ,2.+3.*I]	0.0291956 + 0.513051 I

На рис. 6.8 представлены графики ряда гипергеометрических функций, перечисленных выше. 

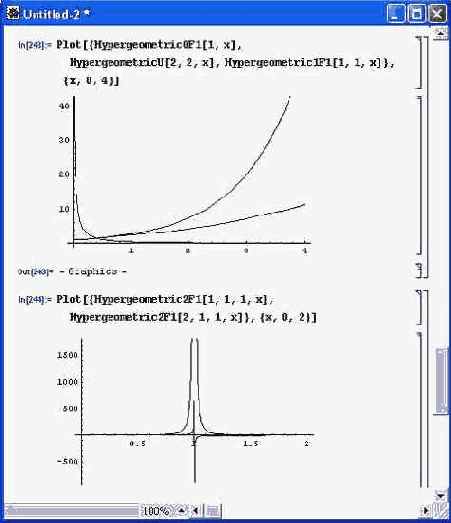
Рис. 6.8. Графики гипергеометрических функций

Следует отметить, что число этих функций в ядре новых версий даже несколько сокращено по сравнению с предшествующими версиями. Убраны довольно редко используемые функции, в имени которых имеется слово Regularized.

Эллиптические интегралы и интегральные функции

В ядро системы Mathematica входят эллиптические функции и функции вычисления эллиптических интегралов:

EllipticE [m] — полный эллиптический интеграл Е(т); EllipticE [phi, m] — эллиптический интеграл второго рода Е(Ф\т); EllipticExp [u, {a, b}] — обобщенный экспоненциал, связанный с эллиптической кривой у ² = х ³ + ах ² + bx, EllipticExpPrime [и, {а, Ь}] — производная по первому аргументу EllipticExp[u, {a, b}]; Elliptic? [phi, m] — эллиптический интеграл первого рода Р(Ф\т); EllipticK[m] — полный эллиптический интеграл первого рода К(т)\ EllipticLog [ {х, у}, {а, Ь}] — обобщенный логарифм, связанный ц эллиптической кривой у ² = л ³ + а х ² + b т, EllipticNomeQ [m] — возвращает значение q = Exp[-PiEllipticK[l - m]/EllipticK[m]]; Elliptic?! [n, phi, m] — эллиптический интеграл третьего рода П(и; Ф\т); Elliptic?! [n, m] — полный эллиптический интеграл П(п|т); EllipticTheta [i, z, q] — эллиптическая тета-функция &.(z, q), где i = i, 2, 3 или 4; EllipticThetaC [u, m] — эллиптическая тета-функция Невилла $ _с (и, т); EllipticThetaD [u, m] — эллиптическая тета-функция Невилла $ _d (u, m); EllipticThetaN [u, m] — эллиптическая тета-функция Невилла $ _п (и, ^m ) ^; EllipticThetaPrime [i, z, q] — производная по второму аргументу эллиптической тета-функции в .(z, q), где i= I, 2, 3 или 4; EllipticThetaS [u, m] — эллиптическая тета-функция Невилла u _s (w, т); FresnelCfx] — интеграл Френеля С(х), FresnelS[x] — интеграл Френеля S(x); InverseJacobi** [v, m] — обратная эллиптическая функция Якоби с обобщенным названием **. Возможны следующие наименования для **: CD , CN, CS, DC, DN, DS, NC, ND, NS, SC, SD И SN; JacobiAmplitude [u, m] — амплитуда для эллиптических функций Якоби; Jacobian — опция для FindRoot; может применяться для указания якобиана системы функций, для которых ищется корень; Jacob!** [u, m] — эллиптическая функция Якоби с обобщенным именем **, которое может принимать значения CD, CN, CS, DC, DN, DS, NC, ND, NS, SC, SD и SN; JacobiSymbol [n, m] — символ Якоби от n и in; JacobiZeta [phi, m] — дзета-функция Якоби Z(Ф|m); WeierstrassP [u, g2, g3] — эллиптическая функция Вейерштрасса Р, WeierstrassPPrime [u, g2, g3] — производная эллиптической функции Вейерштрасса Р'по переменной и. Приведем примеры использования некоторых из этих функций.

Эллиптические функции (интегралы) широко используются в оптических расчетах и в астрофизике. На рис. 6.9 показаны графики некоторых эллиптических функций.

Рисунок 6.10 показывает построение контурного графика на комплексной плоскости с параметрическим заданием функций, выраженных через функцию Якоби и эллиптические интегралы. Нетрудно заметить, что график описывает довольно сложную и специфическую поверхность, содержащую периодические пики и впадины.

Читателю рекомендуется просмотреть ряд других примеров на использование функций данного раздела (например, в справочной базе данных системы Mathematica).

Рис. 6.9. Графики некоторых эллиптических функций

Рис. 6.10. Контурный график с параметрическим заданием комбинированной функции, содержащей функцию Якоби и эллиптические интегралы

 

Функции Эйри

  Функции Эйри представляют собой независимые решения линейного дифференциального уравнения w"- zw = 0. В Mathematica эти функции представлены следующим набором:

AiryAi [z] — возвращает значение функции Эйри Ai(z); AiryAiPrime [ z ] — возвращает значение производной функции Эйри Ai '(z); AiryBi [z] — возвращает значение функции Эйри Bi(z); AiryBiPrime [z] — возвращает производную функции Эйри Bi'(z). Ниже представлены примеры на вычисление функций Эйри.

Ввод (In)	Вывод (Out)
AiryAi [2. +3.*I]	0.00810446 + 0.131178 I
AiryAi[l.]	0.135292
AiryBi [2. +3.*I]	-0.396368 - 0.569731 I
AiryBiPrime [2 . +3 . *I]	0.349458 - 1.10533 I

С функциями Эйри связаны многие специальные математические функции. Эта связь проявляется и при выполнении различных математических операций над функциями Эйри:

D[AiryAi[x],х]

AiryAiPrime[x]

Integrate[AiryBi[x],x]

{xGamma[1/3 ] HypergeometricPFQ[{1/3 }, {2/3,4/3}, x3/9]} /{3 31/6 Gamma [ 2/3 ] Gamma [ 5/3 ]}

{ x2Gamma[1/3 ] HypergeometricPFQ[{1/3 }, {2/3,4/3}, x3/9]} /{3 35/6 Gamma [ 4/3 ] Gamma [ 5/3 ]}

Series[AiryBi[x],{x,0,5}]

{1 /31/6xGamma[2/3]}+ {31/6x /Gamma[1/3]}+ {x3 /631/6Gamma[2/3]}+{x4 /435/6Gamma[1/3]}+O[x]6

Графики функций, Эйри представлены на рис. 6.11.

Нетрудно заметить, что при х < 0 они имеют колебательный характер.

Рис. 6.11. Графики функций Эйри (сверху) и их производных (снизу)

 

Бета-функция и родственные ей функции

Класс бета-функций, имеющих специальное интегральное представление, в Mathematica представлен следующим набором:

Beta [а, b] — эйлерова бета-функция В(a, b); Beta[z, а, b] — неполная бета-функция; Beta[z0, zl, a, b] — обобщенная неполная бета-функция Beta [z1, a, b] - Beta[z0, а, b]; BetaRegularized [z, a> b] — регуляризированная неполная бета-функция I(z,a,b) = Betafz, a, b]/Beta[a, b]; BetaRegularized [z0, zl, a, b]—регуляризированная обобщенная неполная бета-функция I(z1l,a,b) - I(z0, a, b). Поимепы на вычисление этих функций представлены ниже.

Ввод (In)	Вывод (Out)
Beta[l.,2.]	0.5
Beta[l.,2.,3.]	0.0833333
Beta[2.+3.*I,4.+6.*I,l,2]	4. - 12. I
BetaRegulari zed [0.1,1,2]	0.19

 

Специальные числа и полиномы

Для вычисления специальных чисел и полиномов служит следующая группа функций:

BernoulliB [n] — n-е число Бернулли; BernoulliB [n, х] — полином Бернулли n-й степени; Binomial [n, m] — биномиальный коэффициент; Cyclotomic [n, х] — циклотомический полином порядка п по переменной х; EulerE[n] — n-е число Эйлера; EulerE[n, х] — n-й полином Эйлера; EulerPhi [n] — эйлерова функция сумм ф(n) — количество положительных целых чисел, не превосходящих п и взаимно простых с и; Fibonacci [n] — n-е число Фибоначчи; Fibonacci [n, х] — полином Фибоначчи F _n (x); Multinomial [n1, n2, . . . ] — мультиномиальный коэффициент (n! + n2 + . . .) !/(n1! n2! ...); NBernoulliB [n] — численное значение n-го числа Бернулли; NBernoulliB [n, d] — n-е число Бернулли с n?-цифровой точностью представления; Pochhammer [а, n] — символ Похгамера; StirlingSl [n, m] — число Стирлинга первого рода; StirlingS2 [n, m] — число Стирлинга второго рода. Ниже представлены примеры вычисления данных функций.

На рис. 6.12 показаны графики полиномов Бернулли и циклотомического полинома различных порядков.

Рис. 6.12. Графики полиномов Бернулли (сверху) и циклотомических полиномов (снизу)

Обратите внимание на то, что здесь использована функция Plot, модифицированная пакетом расширения plot.m, который будет описан в уроке 10. Эта функция позволяет автоматически строить графики ряда функций с линиями разного стиля, что облегчает их распознавание.

На рис. 6.13 представлены графики полиномов Эйлера EulerE разного порядка п.

Помимо описанных выше, в ядро системы входит также ряд других, менее распространенных функций. Они описаны в приложении.

По числу встроенных специальных математических функций Mathemafica заметно превосходит другие системы компьютерной математики. При этом все такие функции могут участвовать в символьных преобразованиях. Это делает системы Mathematica предпочтительными при решении задач, в которых часто встречаются специальные математические функции. В то же время надо отметить, что многие специальные функции системами Mathemafica вычисляются только для целого порядка.

Рис. 6.13. Графики полиномов Эйлера разного порядка

 

Что нового мы узнали

В этом уроке мы научились:

Вычислять ортогональные многочлены. Вычислять интегральные показательные и родственные им функции. Вычислять гамма- и полигамма-функции. Работать с функциями Бесселя разного рода и порядка. Вычислять гипергеометрические функции. Вычислять эллиптические интегралы и интегральные функции. Вычислять функции Эйри. Вычислять бета-функцию и родственные ей функции. Использовать специальные числа и полиномы.

 

---

---