Знакомство с системой Mathematica

После того как запустим систему Mathematica 5, получится примерно то что изображено на рис. 2.1. Большое белое окно слева- блокнот. Именно в него вводится информация, и именно в нем отображаются результаты. Окно в середине - заставка-приветствие и справка. Окно справа - панель для ввода математических символов греческих букв и т.п. После запуска системы Mathematica в блокнот можно вводить информацию.

Если же по каким-либо причинам активным оказалось другое окно, щелкнув в белом рабочем поле, переключитесь на окно ввода системы Mathematica Введите 2+2 и нажмите комбинацию клавиш <Shift+Enter> (т.е. одновременно клавиши <Shift> и <Enter>).

В окне системы вы увидите следующее (рис. 2.2).

In[1]:=2+2

Out[l]=4

Рис. 2.1. Вот что отображается на экране после запуска системы Mathematica

Возможно, вам пришлось подождать (обычно, не более нескольких секунд). Но не огорчайтесь, это происходила загрузка ядра системы — дальше будет веселей. Например, 10 ! вычисляется практически мгновенно. Для этого нужно набрать 10! и нажать <Shift+Enter>. В результате получим следующее.

In[2]:= 10!

Out[2]= 3628800

Значение 100! можно вычислить, установив двойным щелчком курсор ввода в строке In [2]:= 10! и добавив еще один 0, в результате чего получим 100!

После <Shift+Enter> будет отображено следующее.

In[3]:= 100!

Out[3]=

9332621544394415268169923885626670049071596826438162146859296389521759

9993229915608941463976156518286253697920827223758251185210916864000000

000000000000000000

Рис. 2.2. Вот что появляется в окне ввода системы Mathematica после вычисления 2+2

Арифметические действия над числами

Арифметические действия в системе Mathematica обозначаются как обычно: + (сложение), - (вычитание), * (умножение), / (деление), ^ (возведение в степень).

Впрочем, иногда вместо * достаточно набрать пробел. С делением, правда, есть одна закавыка. Вычислим, например, 10/2.

10/2

Получилось! (Здесь и далее опускаются эти надоедливые In [...]:= и Out [...]=.) Но вот вычисление 22/7 даст

22/7

22/7

Результат, конечно, точный, но несколько тавтологичный. Как же получить десятичное приближение? Для этого достаточно сделать хотя бы одно число вещественным, поставив, например, точку после 22 или 7.

22/7.

3.14286

Есть и другой способ: явно применить функцию N, дающую приближенное численное значение аргумента. (Аргументы функций заключаются в квадратные скобки.)

Для этого введите N[22/7] и в результате получится 3.14286

Функция N позволяет с необходимой точностью вычислять некоторые математические константы и использовать их. Например:

N[Pi]

3.14159

Чтобы вычислить число n со 100 значащими цифрами, укажите нужное количество значащих цифр вторым аргументом функции N.

N[Pi,100]

3.14159265358979323846264338327950288419716939937510582097494459230781

6406286208998628034825342117068

Вот как, например, можно решить известную классическую задачу: какое число больше, е^π или π^e.

N[Е^Pi-Рi^Е, 10]

0.6815349144

Как видите, е^π > π^е. Провести соответствующие вычисления (вместе с оценками точности) вручную не так уж и просто, поэтому обычно первокурсники при решении этой задачи используют свойства функций. Конечно же, в системе Mathematica предусмотрены и функции.

Функции

В системе Mathematica имеется множество математических функций, их имена вполне естественны, за тем исключением, что имена всех встроенных функций начинаются с прописной буквы. Кроме того, не забывайте, что аргументы функций заключаются в квадратные скобки. Ну, и, конечно же, помните о том, что здесь тригонометрические функции называются так, как к этому привыкли американцы: например, вместо привычного для нас tg (тангенса) в системе Mathematica указывается Tan. Ниже приведены некоторые примеры — выполните сами те из них, которые сочтете интересными.

Ехр[3]-Е^3

Ничего неожиданного. Но это не арифметика. Числовые значения здесь не вычислялись. Поэтому сразу получился точный результат. Если бы вычислялись значения, получилось бы нечто совсем иное.

N[Exp[3] ,20]-N[Е^3,20]

0. х10^-19

А вот модуль перехода от натуральных логарифмов к десятичным.

N[Log[10,E],100]

0.43429448190325182765112891891660508229439700580366656611445378316586

46492088707747292249493384317483

А ниже вычислены sin 1° и cos 1° (Улугбеку они бы очень пригодились).

N [Sin [Pi/180] ,100]

0.0174524064372835128194-1897851631619247225272030713964268361242764059

738420392807004200192679102134691

N[Cos[Pi/180],100]

0.99984769515639123915701155881391485169274031058318593965832071451153

91811033372153972993952881103455

Как видим, с тригонометрией все в ажуре! Давайте теперь проведем вычисление с корнями, — вычислим приближенное значение числа 2^√2, столь излюбленного специалистами по математической логике.

N[2ASqrt[2],100]

2.66514414269022518865029724987313984827421131371465949283597959336492

0446178705954867609180005196417

Конечно, то же самое можно сделать и иначе.

N[2^(2^(1/2) ),100]

2.66514414269022518865029724987313984827421131371465949283597959336492

0446178705954867609180005196417

Можно также ввести переменную и написать так:

х=2^(1/2);N[2^х,100]

2.66514414269022518865029724987313984827421131371465949283597959336492

0446178705954867609180005196417

Говоря о корнях, не могу удержаться, чтобы не показать вам вот это:

(-1)^(1/2)

Так что этот калькулятор и с комплексными числами справляется без труда! Но прежде чем переходить к алгебре, полезно хотя бы бегло познакомиться с блокнотом и меню системы Mathematica.

Блокнот и меню

Чтобы упростить набор и вычисление выражений, рассмотрим возможности интерфейса (оболочки) системы Mathematica. Чтобы сохранить протокол расчетов (блокнот), из меню Файл (File) выберите пункт Сохранить Как (Save As) и запишите блокнот в файл, например в файл myl (желательно в своем каталоге). Чтобы повторить какое-либо вычисление, достаточно двойным щелчком установить курсор вставки в соответствующую строку и нажать <Shift+Enter>. Это же можно сделать иначе: установите I-образный курсор на квадратную скобку справа от формулы (курсор при этом изменит свой вид) и щелкните один раз. Скобка "почернеет". Это значит, что вы выделили ячейку, содержащую нужную вам формулу. Теперь выберите в меню системы Mathematica пункт Ядро<=>Вычисление^Вычислить Ячейки. После этого будут вычислены выделенные ячейки. При желании выделенные ячейки можно копировать и размножать обычными для систем с графическим интерфейсом методами (с помощью кнопок или меню). То же самое относится не только к ячейкам целиком, но и к их частям. Эти методы помогают записывать алгебраические выражения.

Алгебраические преобразования

Давайте посмотрим, как система Mathematica справляется с раскрытием скобок в степенях. Для этого служит функция Expand.

Упростим предыдущий результат.

Simplify[%]

 (а + b + с)⁵

Разложим на множители алгебраическое выражение а¹⁰+ b¹⁰. Для этого служит функция Factor.

Factor[а^10 +b^10]

(а² + b²) (а⁸-а⁶b² + а⁴b⁴-а²b⁶ + b⁸)

Теперь подставим а = u, b = у в предыдущий результат.

%/. {a->u, b -> v}

(u² + v²) (u⁸ - u⁶ v² + u⁴ v⁴ - u² v⁶ + v⁸)

Заметьте, что полученный на предыдущем шаге результат обозначен символом %, после него следует/. и список подстановок {a->u, b -> v}.

Все это показывает, что система Mathematica вполне справляется с алгебраическими операциями. Но зачастую полученный результат (выражение, функцию) нужно представить в виде графика.

Построение графиков

Система Mathematica богата графическими возможностями. Рассмотрим на примерах построение хотя бы некоторых, наиболее часто встречающихся типов графиков.

Построение графиков функций одной переменной

Построение графика одной функции, заданной аналитически

Вот как можно построить график функции синус.

Построение графиков нескольких функции, заданных аналитически

Вот как можно построить график нескольких функций.

Построение графика функции, заданной параметрически

Окружность, как известно, не является графиком ни одной однозначной функции. Тем не менее, она может быть задана параметрически. Например, вот так:

Конечно, масштабы по осям здесь разные, и потому окружность изображена как эллипс.

А вот фигура Лиссажу.

И еще одна, на этот раз разомкнутая (хотя концы ее найти не так-то просто!) "фигура Лиссажу".

Построение графиков функций двух переменных

Построим, например, график поверхности z — sin(x² у).

А вот параметрически заданный геликоид.

И, наконец, вот еще одно параметрически заданное тело.

Оказывается, совсем не трудно на одном рисунке показать несколько графиков, ранее построенных по отдельности.

Несколько фантастическое сооружение, не правда ли? Но раз уж мы построили несколько графиков функций, не пора ли перейти к тому разделу математики, в котором изучаются функции?

Анализ

Хотя систему Mathematica и подобные ей называют системами компьютерной алгебры, обычно в них так или иначе представлены все фундаментальные разделы математики. Возможности системы Mathematica в области математического анализа очень велики, и надо полагать, что Лейбниц, Ньютон и Эйлер были бы счастливы поэкспериментировать в области анализа с таким инструментом. Мы же в этой главе ограничимся простейшими примерами.

Дифференцирование

Дифференцировать в системе Mathematica. не просто, а очень просто! В качестве аргументов команды (функции) дифференцирования D [., . ] нужно указать ту функцию, которую мы намерены продифференцировать, и ту переменную (или переменные), по которой (которым) берется производная. Вот как вычисляется производная функции хⁿ.

D[х^n,х]

nx^-1+n

А вот так вычисляется частная производная функции sin(xyz) по переменной z.

D[Sin[x у z],z]

 х у Cos[х у z]

Смешанные частные производные также вычисляются без проблем.

D[Sin[x у z],z,y,x,x]

-5 х у2 z2 Cos [х у z] -

4 у z Sin [х у z] + х2 у3 z3 Sin [х у z]

Это же можно записать иначе.

D[Sin[x у z], {x,2},y,z]

-5 х у2 z2 Cos [х у z] -

4yzSin[xyz]+x2y3z3Sin[xyz]

Полный дифференциал вычисляется посредством команды Dt:

Dt[Sin[x у z] ]

Cosfx у z](у z Dt[x]+x z Dt[y]+x у Dt[z])

где Dt [x], Dt [у] и Dt [z] — дифференциалы переменных х, у и z.

Естественно, что команда Dt применяется и для вычисления полных производных функций многих переменных.

Dt[f[Sin[х у z]],х]

Cos[xyz](yz + xzDt[y, x] +xyDt[z, x] )

 f [Sin[xyz]]

Здесь Dt [y,x] и Dt [z,x] — полные производные переменных у и г по переменной х. Но следующий результат можно назвать правильным лишь формально.

D[Abs[x],x]/.x->l

Abs'[l]

Тут система Mathematica села в калошу. Она знает, что функция [x] — недифференцируемая в точке х = 0, но фактически отказывается вычислять ее производную даже в тех точках, где она дифференцируема. Так спокойнее!?

Интегрирование

Неопределенные интегралы, или первообразные

Интегрирование в системе Mathematica (как и в жизни) сложнее дифференцирования. Впрочем, формально все просто: неопределенный интеграл вычисляют посредством команды Integrate:

Заметьте, что здесь не учтен случай n = -1. Конечно же, неберущиеся интегралы не берутся.

А вот более сложный пример.

Для человека это уже не совсем просто. Впрочем, в ранних версиях система Mathematica взять этот интеграл не могла.

Определенные интегралы

Команда Integrate умеет вычислять и определенные интегралы, а для тех, которые с ее помощью не берутся, имеется команда NIntegrate, позволяющая вычислять определенные интегралы приближенно. Рассмотрим пример.

Integrate[3х^2, {х,0,1}]

В необходимых случаях выполняются проверки.

Как видите, система Mathematica рассмотрела даже случаи комплексного n. Но есть ведь неберущиеся интегралы... Система не отступает даже перед ними.

Integrate[Sin[Sin[x]],{х,0,Pi}]

π StruveH[0,1]

В данном случае система Mathematica выразила значение интеграла через константу и значение специальной функции. Но можно, конечно, вычислить и приближенное значение интеграла.

NIntegrate[Sin[Sin[x]] , {х,0,Pi}]

 1.78649

Повторные интегралы

Конечно, система Mathematica может вычислять и повторные интегралы.

Суммы

Для вычисления сумм в системе Mathematica имеется команда Sum. Вот как вычисляется, например,

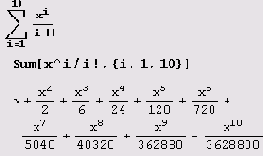
А теперь рассмотрим вычисление двойной суммы

Разложение в ряд Тейлора

Вот как система Mathematica разлагает функцию Sin в ряд Тейлора.

Чтобы отбросить остаточный член, можно воспользоваться командой Normal.

Конечно, все это можно сделать сразу.

А теперь построим графики синуса и пяти его разложений по формуле Тейлора.

Вычисление пределов

Система Mathematica может вычислять пределы — замечательные и не очень.

Но при попытке подставить 0 в выражение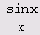

Однако при других значениях х значение выражения будет вычислено без проблем.

А вот как вычисляется еще один замечательный предел.

Однако при вычислении пределов нужно проявлять осторожность. Чтобы разобраться, в чем тут дело, рассмотрим следующий (по существу, тривиальный) пример:

Предела (двустороннего) здесь не существует, но

Таким образом, в данном случае система Mathematica под видом двустороннего предела пытается подсунуть односторонний предел. Честно говоря, это несколько обескураживает и довольно досадно, поскольку с вычислением односторонних пределов система Mathematica в данном примере справляется без труда.

Дело в том, что в некоторых случаях система Mathematica ограничивается односторонними (например, левосторонними, когда переменное приближается слева, т.е. возрастает, или правосторонними, когда переменное приближается справа, т.е. уменьшается) пределами, а для правосторонних пределов нужно указывать Direction->-l. Но разве это хорошо?!

В предыдущих версиях (2.2) были проблемы с пределом

К счастью, уже в версии 3.0 этот недостаток был устранен.

Более того, система Mathematica может вычислить даже следующие пределы.

Списки и линейная алгебра

В линейной алгебре часто рассматриваются объекты, сконструированные из других объектов. Вектор, например, часто представляется в виде списка чисел (являющихся его координатами в некотором базисе). Матрицы — это прямоугольные таблицы, в каждой клетке которых находится элемент некоторого кольца. Тензоры же являются просто многомерными таблицами. Как же такие составные объекты представляются в системе Mathematica? Оказывается, что для конструирования составных объектов произвольной сложности в системе Mathematica используются списки. Именно их мы и рассмотрим сейчас.

Списки

Список — это заключенная в фигурные скобки произвольная последовательность объектов, в которой объекты отделяются друг от друга запятыми. Именно списки используются для конструирования составных объектов. Иными словами, все составные объекты являются списками, причем конструкция объекта отражается в конструкции списка. Самый простой список — линейный. Строка (или столбец) представляется в виде линейного списка. Матрица, являющаяся списком строк (или столбцов), представляется в виде линейного списка линейных списков. Конечно же, с помощью списков можно строить и более сложно устроенные объекты, такие как деревья или различные разновидности графов.

Векторы

Из всего многообразия составных объектов линейной алгебры проще всего устроены векторы. Поэтому не удивительно, что именно они представляются самым простым видом списков — линейными списками. Фактически вектор представляется как список своих координат. Вот как, например, представляется стандартный базис в R³: e1 = {1, 0, 0}; е2 = {0, 1, 0}; е3 = {0, 0, 1}. А вот так представляется вектор u = {а,b,с} с координатами u = {а,b,с}: u = {а,b,с}. Давайте разложим этот вектор по стандартному базису и посмотрим, что получится.

е1={1,0,0}; е2={0,1,0 };е3={0,0,1),u={a,b, с};

 v=a*e1+b*e2+ с*е3 (а,b,с)

Как видите, мы записали разложение вектора u = (а,b,с) по стандартному базису и, выполнив сложение трех векторов (проекций вектора u = {а,b,с) на оси координат), получили вектор v = {a,b,c}. (Как и следовало ожидать, вектор v = u.) Как видим, операции над векторами обозначаются естественным образом. Давайте теперь вычислим скалярное произведение векторов v и u.

u.v

а2 + b2 + с2

Естественно, это скалярный квадрат вектора u. Теперь давайте вычислим скалярное произведение вектора u и единичного орта е3.

u.е3

с

Как и следовало ожидать, оно равно соответствующей координате вектора u.

Матрицы

В системе Mathematica матрицы представляются в виде списков строк, т.е. в виде списков списков. Вот пример задания матрицы. Матрица задается как список списков.

m1={{1,1,1,1},{а,Ь,с,d},{а^2,b^2,с^2,d^2}}

{{1,1,1,1},

{а,b,с,d}, {а2,b2,с2,d2}}

Конечно, привычнее ее видеть как матрицу.

Действия с матрицами и векторами задаются естественным образом. Умножим, например, матрицу на вектор.

А вот как можно умножить матрицу m1 на скаляр t.

Для квадратной матрицы Mathematica позволяет найти определитель, а также обратную матрицу (если, конечно, матрица обратима, т.е. имеет ненулевой определитель), собственные значения и векторы.

Пусть

Найдем определитель

Det[m2]

Поскольку он ненулевой, можем найти обратную матрицу.

Произведение матрицы на ее обратную должно быть единичной матрицей. Давайте проверим.

Так и есть!

Однако обратите внимание: произведение матриц обозначается точкой. Дело в том, что произведение m3 * m2 тоже имеет смысл, но это поэлементное произведение списков, а не произведение матриц! Убедимся в этом.

Собственные значения и векторы находятся без особых сложностей.

Да, пока не совсем понятно... Но не огорчайтесь, при необходимости собственные числа и собственные векторы можно найти приближенно. Вот как найти ответ с машинной точностью.

Но все же, что же это такое `Root? Оказывается, Root[f, k] — это k-й корень алгебраического уравнения f [#1] = 0. (Таким образом, f — полином.) Так что, система Mathematica умеет решать уравнения?! Оказывается, да!

Уравнения

Система Mathematica классно решает разнообразные уравнения и их системы.

В системе Mathematica знак равенства (=) в уравнениях представляется посредством

двойного знака равенства (= =). Вот как можно решить уравнение х³ + х - 2 = 0.

Обратите внимание на мнимую единицу в записи двух корней. Как видите, был найден не только вещественный корень, но и комплексные корни. Система Mathematica находит все (вещественные и комплексные) решения алгебраических уравнений степени не выше 4, притом не только с числовыми коэффициентами, но и с параметром.

Конечно, ответ несколько громоздкий. Представьте, если бы вам пришлось искать его самостоятельно!

Решения общего алгебраического уравнения степени 5 или выше через радикалы не выражаются, но всегда могут быть найдены численные их значения. Тем не менее система Mathematica пытается найти точное решение. Например, уравнение х⁵ + х - 2 = 0 система Mathematica решит точно.

А вам слабо? Давайте попробуем решить уравнение х⁵ + х -7 = 0 .

Да, корни уравнения — это его корни... (И, как видите, их пять, что тоже не особенно информативно, если учесть, что многочлен пятой степени.) В данном случае при необходимости можно решить уравнение численно.

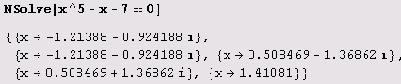
Чтобы решить трансцендентное уравнение, нужно задать начальное приближение к корню. Вот как, например, можно решить уравнение cosx = 2x.

Давайте попробуем решить систему линейных алгебраических уравнений.

А чтобы решить систему трансцендентных уравнений, нужно задать начальные приближения неизвестных.

Система Mathematica умеет решать и дифференциальные уравнения и их системы.

Как видите, решение содержит произвольные постоянные C [1] и С [2]. Можно найти также численное решение задачи Коши для дифференциальных уравнений или их систем.

Правда, решение содержит приближенную функцию (объект InterpolatingFunction). Но этот объект может быть вычислен, как и любой другой объект системы Mathematica. В частности, можно построить график.

Экстремумы функций

Система Mathematica позволяет найти экстремумы функций одной и нескольких переменных. Вот как, например, можно найти локальный минимум функции e^xcosx.

FindMinimum[Exp[x]*Cos[x],(х,0}]

{-0.0670197,{х>-2.35619}}

А вот как можно найти минимум функции sinxcosy .

FindMinimum[Sin[x]*Cos[у],{х,0},{у,0}]

{-1.,{x>-1.5708,y>0.}}

Ну и раз уж речь зашла об экстремумах функций, рассмотрим случай линейных функций.

Линейное программирование

Используя систему Mathematica, нетрудно решить задачи линейного программирования небольшой размерности. Рассмотрим пример.

Правда, если экстремум достигается на границе (а в задачах линейного программирования это случается почти всегда), при использовании функции Maximize выдается предупреждение об этом.

Можно, конечно, пользоваться и функцией ConstrainedMax, но она становится все менее популярной, и система Mathematica предупреждает, что в последующих версиях она может быть удалена.

Впрочем, для решения задачи можно воспользоваться и функцией Nmaximize.

NMaximize[{19x-47y+28z,{x+y+z>0,x+y+z<l,x>0,y>0,z>0}},{x,y,z}]

{28.,{x>0.,y>0.,z>l.}}

Обратите внимание на то, что списки параметров у этих функций разные: у функции Maximize — три параметра, а у NMaximize — только два.

в качестве калькулятора. Но даже

Мы бегло ознакомились с применением системы Mathematica в качестве калькулятора. Но даже из этого беглого знакомства видно, что если это и калькулятор, то очень мощный и интеллектуальный. Немного позже мы узнаем, что он еще и программируемый. Как бы то ни было, с ним стоит познакомиться поближе. И если вы запомнили не все, не огорчайтесь. Ведь начнем мы с самого начала — с чисел.