Алгебра и пакет Mathematica 5
Факторизация чисел Мерсенна
Числами Мерсенна, как известно, называются числа Мn = 2n-1. Как следует из формулы разложения двучлена
an-bn, они могут быть простыми лишь при простом п. При четном
n выражение 2n-1 можно разложить на множители, пользуясь, например,
формулой для разности квадратов. Вот первые три числа Мерсенна: М1= 1; M2 == 3;
M3 = 7. Дальнейшие вычисления поручим системе Mathematica. Для этого напишем программу для разложения чисел Мерсенна, получающихся при
n = 1,2, 3, ..., k.
Сначала давайте решим какой-нибудь конкретный пример. Разложим, например, на множители число
M67. Марен Мерсенн в 1644 году высказал мнение, что это число простое. Однако ошибочность этого утверждения была установлена Э. Люка только в 1875 году. Давайте же посмотрим, сколько времени потребуется системе Mathematica, чтобы справиться с более трудной задачей — разложением на простые множители. Итак, вводим запрос
Factorlnteger[ 2^67-1 ] . и мгновенно получаем ответ.
{193707721,1}, {761838257287,1}}
Вот это да! Mathematica почти мгновенно сделала то, на что математикам потребовалось затратить 231 год!
Теперь можем смело приступить к написанию программы. В качестве последнего числа, разлагаемого на множители, выберем М257. Именно это число было исследовано М. Б. Крайчиком, который установил, что оно составное. Программа может выглядеть так:
Dо[ Print [n, ": ", Factor-Integer [2^n-1] ],{n,257}]
Однако вывод такой программы выглядит несколько "однолинейно".
1 {}
2 {{3,1}}
3 {{7,1}}
4 {{3,1},{5,1}}
5 {{31,1}}
6 {{3,2},{7,1.}}
7 {{127,1}}
8 {{3,1},{5,1},{17,1}}
9 {{7,1},{73,1}}
10 {{3,1},{11,1},{31,1}}
11 {{23,1},{89,1}}
12 {{3,2},{5,1},{7,1},{13,1}}
13 {{8191,1}}
14 {{3,1},{43,1},{127,1}}
15 {{7,1},{31,1},{151,1}}
16 {{3,1},{5,1},{17,1},{257,1}}
17 {{131071,1}}
18 {{3,3},{7,1},{19,1},{73,1}}
19 {{524287,1}}
20 {{3,1},{5,2},{11,1},(31,1),{41,1}}
Кроме того, он и читается с трудом. Поэтому для преобразования вывода в привычную форму лучше всего использовать макрос, написанный на VBA для Word 2002.
Sub Factorization() i
'Обработка списка множителей
Dim strTemp As String
Dim Msg, Style, Title, Help, Ctxt, Response, MyString, R
Msg = "Хотите продолжить ?" ' Вопрос
Style = vbYesNo + vbCritical + vbDefaultButton2 ' Кнопки
Title = "Разложение на множители"' Заголовок окна
Response = vbYes ' Пока ошибки не обнаружены
Selection.Find.ClearFormatting
'Очистка формата в поле поиска With Selection.Find
.Text = "{" ' Что ищем - открывающую скобку
.Forward = True
.Wrap = wdFindContinue
.Format = False
.MatchCase = False
.MatchWholeWord = False
.MatchWildcards = False
.MatchSoundsLike = False
.MatchAllWordForms = False End With Selection.Find.Execute
'Находим открывающую фигурную скобку списка
strTemp = Selection.Text
If strTemp = "{" Then
' Если нашли скобку, обрабатываем список
Selection.Delete Unit:=wdCharacter, Count:=1
' Удаляем скобку Do '
В цикле обрабатываем все элементы списка
Response = Multiplier '
Обработка множителя и его показателя
If Response = vbYes Then
Selection.MoveRight Unit:=wdCharacter, Count:=1, _
Extend:=wdExtend
strTemp = Selection.Text
' Выбираем очередной символ
If strTemp = "," Then
' Это должна быть запятая
Selection.Delete Unit:=wdCharacter, Count:=l
' Удаляем ее
Selection.Font.Reset ' Сбрасываем форматирование
Selection.InsertSymbol Font:="Symbol",
_ CharacterNumber:=-3916, Unicode:=True
' Знак умножения
End If ' Запятую заменили знаком умножения Else
R = MsgBox("***Ошибка: неправильно записан множитель." _
+ Msg, Style, Title) End If
Loop While strTemp = ","
And (Response = vbYes)
Выполняем цикл, пока не обработаем все
множители 1 или не обнаружим ошибку
•
If strTemp = "}" Then
' Список должен заканчиваться закр. скобкой
Selection.Delete Unit:=wdCharacter, Count:=1
' Удаляем скобку
Else
Response = MsgBox("***0шибка: в конце списка нет } ... " _
+ Msg, Style, Title)
If Response = vbYes Then
' Пользователь выбрал Yes (Да)
MyString = "Yes"
' Запомним, что выбрал пользователь
Else ' Пользователь выбрал No (Нет)
MyString = "No"
' Запомним, что выбрал пользователь
End If End If End If End Sub
Function Multiplier() i
' Обработка множителя (и его степени)
Dim strTemp As String
Dim Msg, Style, Title, Help, Ctxt, Response, MyString
Msg = "Хотите продолжить ?"
' Вопрос к пользователю
Style = vbYesNo + vbCritical + vbDefaultButton2' Кнопки
Title = "Очередной множитель: степень простого"
'Заголовок окна
Response = vbYes ' Пока ошибки не обнаружены
' Selection.MoveRight Unit:=wdCharacter, Count:=l,
Extend:=wdExtend strTemp = Selection.Text
' Выбираем очередной символ If strTemp = "{" Then
' Если открывающая скобка - начало множителя
Selection.Delete Unit:=wdCharacter, Count:=1
' Скобку удаляем Selection.MoveRight Unit:=wdWord,
Count:=l, Extend:=wdExtend Selection.MoveRight
Unit:=wdCharacter,
Count:=1 ' Основание Selection.MoveRight Unit:=wdWord,
Count:=1, Extend:=wdExtend strTemp = Selection.Text
' Основание отделяется , от показателя
If strTemp = "," Then
' Разделитель нашли PowExp
' Обрабатываем показатель
Selection.MoveRight Unit:=wdCharacter, Count:=l, _
Extend:=wdExtend
strTemp = Selection.Text
' Этот символ завершает множитель
If strTemp = "}"
Then ' Это должна быть закрывающая скобка
Selection.Delete Unit:=wdCharacter, Count:=1
' удалить ее Else
' Но ведь в конце же должна быть закрывающая скобка
Response = MsgBox("***0шибка в сомножителе: нет } ... " _
+ Msg, Style, Title)
If Response = vbYes Then
' Пользователь выбрал Yes (Да)
MyString = "Yes" ' Запомним, что выбрал пользователь
Else ' Пользователь выбрал No (Нет)
MyString = "No"
' Запомним, что выбрал пользователь
End If End If Else ' Иначе - а где же запятая?
Response = MsgBox("***0шибка в сомножителе: нет , ... " _
+ Msg, Style, Title) If Response = vbYes Then
' Пользователь выбрал Yes (Да)
MyString = "Yes"
'Запомним, что выбрал пользователь
Else ' Пользователь выбрал No (Нет)
MyString = "No" ' Запомним, что выбрал пользователь
End If End If
Else ' Иначе - а где же открывающая скобка ?
Response = MsgBox("***0шибка в сомножителе: нет { ... " _
+ Msg, Style, Title) If Response = vbYes
Then ' Пользователь выбрал Yes (Да)
MyString = "Yes"' Запомним, что выбрал пользователь
Else ' Пользователь выбрал No (Нет)
MyString = "No" ' Запомним, что выбрал пользователь End If
End If
Multiplier = Response
End Function
Sub PowExpO
i
' Обработка пokaзaтeля
t
Dim strTemp As String
Selection.Delete Unit:=wdCharacter, Count:=1
' Удаляем символ Selection.MoveRight Unit:=wdWord,
Count:=l, Extend:=wdExtend strTemp = Selection.Text
' Это и есть показатель If strTemp = "1"
Then ' Если показатель равен 1
Selection.Delete Unit:=wdCharacter, Count:=1
' Удаляем его
Else ' В противном случае форматируем его как надстрочный
With Selection.Font
.Superscript = True 'Надстрочный
End With Selection.MoveRight
Unit:=wdCharacter, Count:=1
Selection.Font.Reset 'Восстановить стиль
End If End Sub
Этот макрос преобразует разложение
{{3,3}, {5,1}, {7,1}, {13,52},{17,1},{19,551},
{37,1},{73,1},{109,1}, {241,1},{433,1},{38737,1}}
к более привычному виду:
33x5x7xl352xl 7X19S51X37X7 3x109x241x433x38737
Теперь можем воспользоваться созданной программой и составить таблицу разложения чисел Мерсенна на простые множители (табл. Б. 10).
Довольно интересно наблюдать за тем, как Mathematica составляет эту таблицу. Первая сотня чисел Мерсенна разлагается практически мгновенно. Незначительные задержки происходят только на второй сотне. Интересно отметить, что эти задержки в пределах второй сотни происходят и при составных n, т.е. в случаях, когда человек воспользовался бы уже вычисленными ранее разложениями. Это свидетельствует о том, что Mathematica в данном случае не пользуется формулой разности степеней. Впрочем, первая существенная задержка происходит только при значении n = 227 (простое). Однако почти сразу же за ней Mathematica сталкивается с рядом незначительных трудностей, которые она быстро преодолевает, но при n = 251 (простое) происходит вторая существенная задержка. Однако поистине удивительно, что самая существенная задержка происходит, казалось бы, в очень простом случае — при n = 254. Ведь при этом значении и число Мерсенна представляет собой разность квадратов, так что фактически число сразу разлагается на множители, которые только на единицу отличаются от корня квадратного из исходного числа. Так что количество цифр в подлежащих разложению числах фактически на первом же шаге уменьшается вдвое! Кроме того, одно из этих чисел представляет собой число Мерсенна М127, которое уже было разложено на множители ранее (точнее, была установлена его простота). Однако если пропустить это число, то разложения М127 и М256 получаются достаточно быстро.
А вот чтобы на нынешних ПК средней мощности разложить число М. Б. Крайчика (Л/257) прямым применением функции FactorInteger, придется подождать несколько часов.
Давайте теперь обсудим, почему все же для системы Mathematica разложить число Крайчика проще, чем М127. Дело в том, что хотя по формуле разности квадратов M254 = M127х(2127+1), система Mathematica об этом не подозревает, и потому она должна сначала найти множитель M127, а затем доказать его простоту. Кроме того, нужно еще разложить на множители число 2'27+1. Это, правда, чуть легче, поскольку очевидно, что оно делится на 3. Впрочем, необходимость в разложении чисел вида 2"+1 в теории кодирования возникает столь часто, что стоит испробовать возможности системы и в этом случае.
Факторизация чисел вида 2n+1
Среди чисел вида 2n+1 простые, можно сказать, почти не встречаются, ведь число такого вида может быть простым только тогда, когда n является степенью двойки:
n = 2*. Такие числа называются числами Ферма:
Fn = 22n +1.
Пьер Ферма утверждал, что все такие числа просты. Однако Л. Эйлер установил, что F5= 232+l делится на 641. Давайте попытаемся составить таблицу разложения чисел вида 2"+1 на простые множители. В свое время (70-е годы прошлого столетия) Дональду Кнуту удалось исхитриться и с помощью тождества 2214+1 = (2107-254-Н) (2|07+254-Н) и мощного (для того времени) компьютера факторизовать это число. Давайте попробуем и мы. Вот необходимая программа.
Do[ Print[n,":",FactorInteger[2^n+1]], {n, 214} ]
Даже на весьма слабеньком компьютере построение нужной нам таблицы занимает всего лишь несколько минут .
Да, результат очень даже впечатляет! Но давайте вспомним, что эта таблица нам понадобилась потому, что (с точки зрения компьютера!) у нас не хватило терпения дождаться разложения числа Мг54 прямым применением функции Factorlnteger. Теперь мы без труда можем написать нужное нам разложение.
М254 = 3x56713727820156410577229101238628035243XMi27.
Факторизация чисел вида 2n-7
Наряду с разложениями чисел Мерсенна и чисел вида 2n+1, представляет интерес также факторизация чисел вида 2n7-. Так как эти числа будут натуральными только при n > 2, то в программу нужно вставить начальное значение
n, равное 3. Поэтому программа будет иметь следующий вид:
Do[Print[n, ":",Factorlnteger[2^n-7]],{n,3,50}]
Даже на весьма слабеньком компьютере построение нужной нам таблицы занимает всего лишь несколько секунд .
Как видим, при 3<и<50 среди чисел вида 2n-7 простое только одно, соответствующее значению n = 39. Заметные задержки (несколько секунд) при факторизации чисел такого вида возникают лишь при n>200.
Факторизация чисел, десятичная запись которых состоит из n единиц
До сих пор мы изучали быстродействие функции FactorInteger на аргументах, близких к 2n. В двоичной системе счисления запись таких чисел содержит много нулей или единиц подряд. Число Мерсенна
Mn, например, записывается п единицами, а число 2n+1 — двумя единицами, между которыми стоит л-1 нуль (рассматриваем случай
n > 0). Поэтому может показаться, что функция FactorInteger столь эффективна лишь для чисел, которые имеют специальный вид в двоичной системе счисления. Поэтому давайте изучим возможности этой функции по факторизации больших чисел видов, более случайных с точки зрения теории чисел. Попытаемся разложить, например, числа, десятичная запись которых представляет собой повторение одной и той же цифры л раз. Конечно, если
n =1, то эта цифра повторяется только один раз, и вопрос о разложении решается в уме. С другой стороны, даже если
n> 1, то, разделив такое число на ту цифру, которая повторяется n раз, получим число, десятичная запись которого состоит из л единиц. Так что для факторизации чисел такого вида достаточно иметь таблицу разложения чисел, десятичная запись которых состоит из
n единиц. Обозначим это число через 1n. Как задать такое число? Как легко видеть, число, десятичная запись которого состоит из
n девяток, равно 10n-1. Разделив это число на 9, получим число, десятичная запись которого состоит из л единиц:
(10n-1)/9. Таким образом, мы убедились, что
(10n-1)/9= 1n= 111............................111 («единиц).
Заметим сразу, что такие числа могут быть простыми лишь в том случае, если количество единиц
n в записи такого числа — простое. Действительно, если n = m k, то такое число делится как на число, состоящее из т единиц, так и на число, состоящее из k единиц. Короче говоря, от
m| n => 1m | 1n. (Убедиться в этом очень легко, мысленно выполнив деление "столбиком".)
Теперь несложно написать нужную нам программу.
Do[Print[n,":",FactorInteger[(10^n-1)/9]],{n,70}]
В пределах таблицы простых чисел совсем немного, они получаются лишь при n = 2, 19 и 23. Поэтому при всех четных n число 1 имеет 11 в качестве простого множителя. Несколько сложнее увидеть, что 3k|n=>3k| 1n. (Например, все числа вида 13m делятся на 3, это следует из школьного признака делимости на 3. Аналогично обстоит дело и с числами вида 19m.) Это следует из того, что 3k|1k . Как видим, используя таблицу факторизации чисел вида 1n, составленную с помощью простой программы, совсем несложно подметить простейшие закономерности в разложении данных чисел.
Факторизация чисел вида 10n+1
Теперь, следуя логике изучения чисел, близких к 2n, построим таблицу факторизации чисел вида 10n+1. В десятичной системе счисления запись таких чисел начинается и заканчивается единицей, а между этими единицами стоят нули:
10n + 1 = 1000............................00001 (n-1 нулей).
Вспоминая формулы суммы степеней, сразу замечаем, что такие числа могут быть простыми лишь в том случае, если л является степенью двойки, т.е. если
n = 2k. (При нечетных и, все такие числа делятся, например, на сумму оснований, т.е. на 11.)
Вот программа, которая строит нужную нам таблицу.
Do[Print[n,":",Factorlnteger[10^n+1]],{n,70}]
Факторизация чисел Фибоначчи
Давайте теперь рассмотрим несколько иной пример. Попытаемся факторизовать числа такой последовательности, которая не может рассматриваться как некоторое тривиальное изменение последовательности аn с целым основанием а. В качестве такой последовательности можем выбрать, например, последовательность Фибоначчи. Напомним, что последовательность Фибоначчи рекуррентно определяется так:
F1 = F2 = 1, Fn+2 = Fn+1 +Fn.
Если Fn — простое, то либо n = 4, либо n — простое. Теперь построим таблицу факторизации чисел Фибоначчи.
Для этого напишем программу, в которой предусмотрим вывод не только разложения числа Фибоначчи, но и самого числа.
Do[Print[n,":",Fibonacci[n]], ":",
FactorInteger[Fibonacci[n]]],{n,270}]
Данная таблица недаром содержит числа Фибоначчи Р„ для п вплоть до 300. Дело в том, что до 1963 года (а это совсем недавно с точки зрения многотысячелетней истории теории чисел) было известно, что числа ФибоначчиFn являются простыми для n = 3, 4, 5, 7, 11, 13, 17, 23, 29, 43, 47. Упорные же поиски других простых чисел Фибоначчи в то время никаких результатов не дали. Так что с этой точки зрения наша таблица содержит несколько совсем нетривиальных открытий!
Факторизация дробей
Прочитав заголовок, вы, возможно, скажете: "Раскладывать дроби на простые множители? Да как же это?! Такой операции в арифметике нет!". Действительно, такой операции вроде бы и нет, но вспомните, как часто приходится раскладывать на простые множители числитель и знаменатель одной и той же дроби. И чтобы вы не мучились, по отдельности вызывая функцию
FactorInteger для числителя и знаменателя, можете вызвать ее для всей дроби. Это ведь так удобно! В каком же виде будет представлено разложение? Почти в том же, что и для целых чисел, но только показатели простых множителей знаменателя будут отрицательными. Вот пример:
Factorlnteger[1952/1921]={{2,5},{17,-1},{61,1},{113,-1}}.
Давайте же теперь испытаем функцию FactorInteger в новой роли:
Do[Print[n,":",Factorlnteger[BernoulliB[n]]],
{n,2,102,2}]
Результат, как обычно, представим в виде таблицы. Однако оказывается, что разработанный ранее макрос для преобразования разложения в обычную форму уже не годится. Ведь теперь основания (да и сами показатели) степеней могут быть отрицательными. Поэтому в таких случаях основания нужно взять в круглые скобки. Это учтено в новом макросе.
Sub Factorization()
'Обработка списка множителей
Dim strTemp As String
Dim Msg, Style, Title, Help, Ctxt, Response, MyString
Msg = "Хотите продолжить ?"
' Вопрос
Style = vbYesNo + vbCritical + vbDefaultButton2
'Кнопки
Title = "Разложение на множители"
'Заголовок окна
OptPasteSmartCutPaste = Options.
PasteSmartCutPaste Options.
PasteSmartCutPaste = False
Response = vbYes ' Пока ошибки не обнаружены
Selection.Find.ClearFormatting
' Очистка формата в поле поиска
With Selection.Find
.Text = "{"
' Что ищем - открывающую скобку
.Forward = True
.Wrap = wdFindContinue
.Format = False
.MatchCase = False
.MatchWholeWord = False - .
.MatchWildcards = False
.MatchSoundsLike = False
.MatchAllWordForm? = False
End With Selection.Find.Execute
' Находим открывающую фигурную скобку списка
strTemp = Selection.Text
If strTemp = "{" Then
' Если нашли скобку, обрабатываем список
Selection.Delete Unit:=wdCharacter, Count:=1
' Удаляем скобку
Do ' В цикле обрабатываем все элементы списка
Response = Multiplier
' Обработка множителя и его показателя
Selection.MoveRight Unit:=wdCharacter, Count:=1, _
Extend:=wdExtend
strTemp = Selection.Text
' Выбираем очередной символ
If strTemp = ","
Then ' Это должна быть запятая
Selection.Delete Unit:=wdCharacter, Count:=1
' Удаляем ее Selection.Font.Reset
' Сбрасываем форматирование
Selection.InsertSymbol Font:="Symbol", _
CharacterNumber:=-3916, Unicode:=True
' Знак умножения
End If
' Запятую заменили знаком умножения
Loop While strTemp = ","
And (Response = vbYes)
' Выполняем цикл, пока не обработаем все множители
' или не обнаружим ошибку
If strTemp = "}" Then
' Список должен заканчиваться
' закрывающейся скобкой
(Selection.Delete Unit:=wdCharacter, Count:=1
' Удаляем скобку
Else
Response = MsgBox("***0шибка: в конце списка нет } ... " _
+ Msg, Style, Title)
If Response = vbYes Then
' Пользователь выбрал Yes (Да)
MyString = "Yes"
' Запомним, что выбрал пользователь
Else ' Пользователь выбрал No (Нет)
MyString = "No" .
' Запомним, что выбрал пользователь
End If End If End If
Options.PasteSmartCutPaste" = OptPasteSmartCutPaste
End Sub
Function Multiplier() i
' Обработка множителя (и его степени)
1 Макрос записан 26.10.2003 Яков Шмидский t
Dim strTemp As String
Dim Msg, Style, Title, Help, Ctxt, Response, MyString
Msg = "Хотите продолжить ?"
' Вопрос к пользователю
Style = vbYesNo + vbCritical + vbDefaultButton2
' Кнопки
Title = "Очередной множитель: степень простого"
' Заголовок окна
Response = vbYes ' Пока ошибки не обнаружены
strTemp = Selection.Text
' Выбираем очередной символ
Selection.MoveRight Unit:=wdCharacter,
Count:=l, Extend:=wdExtend
If strTemp = "{" Then
' Если отрывающая скобка - начало множителя
Selection.Delete Unit:=wdCharacter, Count:=1
' Скобку удаляем
Selection.Extend Character:=","
' Расширили выделение до ,
Selection.MoveLeft Unit:=wdCharacter, Count:=1,
Extend:=wdExtend
' Отменили выделение , BaseRepresent
Selection.MoveRight Unit:=wdCharacter, Count:=1
' Основание Selection.MoveRight Unit:=wdCharacter,
Count:=l, Extend:=wdExtend strTemp = Selection.Text
' Основание отделяется , от показателя
If strTemp = "," Then
' Разделитель нашли PowExp
' Обрабатываем показатель
Selection.MoveRight Unit:=wdCharacter, Count:=l, _
Extend:=wdExtend
strTemp = Selection.Text
' Этот символ завершает множитель
If strTemp = "}" Then
' Это должна быть закрывающая скобка
Selection.Delete Unit:=wdCharacter, Count:=1
' -Удалить ее Else
' Но ведь в коде же должна быть закрывающая скобка
Response = MsgBox("***0шибка в сомножителе: нет } ... " _
+ Msg, Style, Title) If Response = vbYes Then
' Пользователь выбрал Yes (Да)
MyString = "Yes"
' Запомним, что выбрал пользователь
Else' Пользователь выбрал No (Нет)
MyString = "No"
' Запомним, что выбрал пользователь
End If End If Else ' Иначе - а где же запятая?
Response = MsgBox("***0шибка в сомножителе: нет , ... " _
+ Msg, Style, Title) If Response = vbYes Then
' Пользователь выбрал Yes (Да)
MyString = "Yes"
' Запомним, что выбрал пользователь
Else ' Пользователь выбрал No (Нет)
MyString = "No"
' Запомним, что выбрал пользователь
End If End If End If
Multiplier = Response End Function
Sub PowExp()
t
' Обработка показателя t
Dim strTemp As String
Selection ..Delete Unit :=wdCharacter, Count :=1
' Удаляем символ
Selection.Extend Character:="}"
' Расширили выделение до }
Selection.MoveLeft Unit:=wdCharacter, Count:=1, Extend:=wdExtend
' Отменили выделение }
strTemp = Selection .'Text
' Это и есть показатель
If strTemp = "1" Then
' Если показатель равен 1
Selection.Delete Unit:=wdCharacter, Count:=l
' Удаляем его Else
' В противном случае форматируем его как надстрочный
With Selection.Font
.Superscript = True 'Надстрочный
End With Selection.MoveRight Unit:=wdCharacter, Count:=1
Selection.Font.Reset 'Восстановить стиль
End If End Sub
Sub BaseRepresent() Dim strTemp As String
strTemp = Selection.Text ' Основание
If Not MultiplierQ(strTemp) Then
' Selection.MoveLeft Unit:=wdCharacter, Count:=l '
Selection.InsertBefore "("
' Перед основанием вставим символ {
Selection.InsertAfter ")"
' А после него вставим символ )
End If
End Sub
Function MultiplierQ(strTemp) ret = True
If Left(strTemp, 1) = "-"
Then ret = False MultiplierQ = ret
End Function
Этот макрос преобразует представление
{{-1,n},{2,-1},{-3,-m},{5,-1},{7,-1},{11,-1}, {13,-1},{31,-1},
{61,-1},{2003,1},{5549927,8},{109317926249509865753025015237911,1}}
в такой более привычный вид.
(-1)nх2-1х(-3)-mх5-1х7-1х11-1х13-1х31-1х
61-1x2003x55499278Х109317926249509865753025015237911
Теперь, пользуясь результатами и макросом, можем составить таблицу . Если нужно разложить только, например, числители, можно воспользоваться следующей программой:
Do:[Print[n,":",Factorlnteger[Numerator[BernoulliB[n]]]],{n,2,102,2}].
Так как это разложение играет чрезвычайно важную роль в доказательстве Последней теоремы Ферма, представим его, как обычно, в виде таблицы.
Эта таблица заслуживает внимания. Прежде всего нужно заметить, она может оказать неоценимую помощь при поиске больших иррегулярных чисел. (Напомню, что простое число р называется регулярным, если на него не делится ни один из числителей чисел Бернулли В2, В4, ..., Вp-3. В противном случае простое число называется иррегулярным.) Иррегулярные простые числа долгое время были причиной ужасных неприятностей для всех, кто занимался доказательством Последней теоремы Ферма. Дело в том, что для регулярных чисел эта теорема была доказана Куммером еще в 1850 году. Это было настоящее торжество ферматистов! Наиболее отчаянные предположили даже, что число иррегулярных чисел конечно, и, таким образом, им оставалось якобы рассмотреть лишь конечное число случаев! Нужно заметить, что их предположение не было лишено оснований. Действительно, в пределах первой сотни есть всего лишь три иррегулярных числа: 37, 59 и 67. (В этом легко убедиться, просмотрев составленную нами таблицу.) Однако в 1915 году Иенсен довольно просто доказал, что множество иррегулярных чисел бесконечно. Тогда-то ферматисты занялись изучением иррегулярных чисел вплотную. В 1965 году Эйхлер существенно продвинулся в поисках доказательства Последней теоремы Ферма, а десять лет спустя, в 1975 году, Брюкнер ввел индекс иррегулярности числа р — количество числителей чисел Бернулли В2, В4, ..., В^, делящихся на р, — и тем самым придал результатам Эйхлера вполне обозримую форму. Понятно, что интерес к таблицам, подобным составленной нами (не без помощи системы Mathematica), значительно возрос. Однако даже в 1985 году, после очередного всплеска интереса к Последней теореме Ферма, когда она была доказана для "почти всех" натуральных показателей, таблица, помещенная в одном из лучших университетских учебников по теории чисел — в учебнике 3. И. Боревича и И. Р. Шафаревича, была доведена лишь до п = 60. Так что едва ли будет преувеличением утверждение, что с помощью системы Mathematica мы составили таблицу, о которой несколько поколений ферматистов могли только мечтать!
Кроме того, эта таблица поможет нам понять, как система Mathematica обращается с дробями. Если число дробное (а именно такими и являются числа Бернулли с четными индексами), то знак дроби относится к числителю. В этом легко убедиться, просмотрев нашу таблицу. Действительно, как мы видели из таблицы разложения чисел Бернулли Вn на простые множители, числа B4n-1 отрицательны, а числа B4n-2 положительны. Точно так же распределены и знаки числителей в таблице разложения числителей чисел Бернулли Вn.
Итак, с помощью функции FactorInteger можем разлагать на простые множители не только натуральные и отрицательные числа, но и дроби, — иными словами, все рациональные числа. Таким образом, кажется, мы научились применять эту функцию ко всем числам, к которым применимо понятие разложения на простые множители. Но возможности этой функции шире. Она умеет еще кое-что. "Как? Неужели... Разве это мыслимо, разлагать на множители комплексные числа?", — возможно, подумаете вы. И не ошибетесь!
Факторизация гауссовых чисел
Напомним, что гауссовыми называются комплексные числа, у которых действительная и мнимая части являются целыми числами. Иными словами, это комплексные числа
а+bi, у которых вещественная (а) и мнимая (b) части представляют собой целые числа. Вот примеры гауссовых чисел:
2, 1+2i, i, -i, 1+i, 1-i, 1+7i, 1+555555i, 9999+444i.
На комплексной плоскости гауссовы числа образуют решетку всех точек с целыми координатами. Гауссовы числа называются в честь К. Ф. Гаусса, который обратил на них внимание еще в 1832 году в работе о биквадратичных вычетах. Именно Гаусс понял важность изучения этих чисел и установил их основные свойства.
Как оказалось, множество гауссовых чисел, рассматриваемое с обычными операциями, образует кольцо, являющееся, конечно, подкольцом кольца (даже поля) комплексных чисел. Кольцо целых гауссовых чисел можно рассматривать как расширение кольца целых чисел Z путем присоединения
i, поэтому это кольцо обозначается Z[i].
В этом кольце делителями единицы являются лишь +1, -1, i и -i. Так что множество делителей единицы в кольце гауссовых чисел конечно. А потому в этом кольце имеет смысл понятие простого элемента, а, значит, можно выполнять разложение элементов этого кольца на простые множители. Нетрудно доказать, что кольцо целых гауссовых чисел евклидово. Поэтому с точностью до делителей единицы разложение на простые множители в нем единственно. Так что кольцо гауссовых чисел (как и всякое евклидово кольцо) является гауссовым, или факториальным.
Нормой комплексного числа называется квадрат модуля, т.е. квадрат длины отрезка, соединяющего комплексное число с началом координат. Иными словами, это сумма квадратов вещественной и мнимой частей комплексного числа:
N(a+bi) = (а+bi)(а-bi) = a2 +b2.
Нечетное простое число р является простым гауссовым числом тогда и только тогда, когда оно дает в остатке 3 при делении на 4: р = 3 (mod 4). Если же р =
3 (mod 4), то р не является простым в кольце целых гауссовых чисел. Не является простым в кольце целых гауссовых чисел и число 2.
Давайте теперь найдем несколько разложений гауссовых чисел на простые множители.
Factorlnteger[5-51]={(-1,1},{1+i,I},{1+2 i,1},{2+i,1}}
FactorInteger[3+1]={{-i,1},(1+i,1},{1+2 1,1)}
FactorInteger[-90-180I]={{1+i,2},{1+2 i,2},{2+i,1},{3,2}}
Factorlnteger[-182-1261]={{1+i,3},{2 + i,3},{7,1}}
FactorInteger[3+I5]={{1+i,1},{4+i,1}}
Factorlnteger[777+1111] ={{-1,1},{1+i,1},{1+6
i,l},{2+i,2},{3,l},{6+i,l}}
Factorlnteger[153+1 374]={{-i,l},{!+4 i,1},{2+i,1},{4+i,1},{8+7
i,l}}
Factorlnteger[7+81]={{7+8i,l}}
Число 7+8 i, как видим, оказалось простым. Заметьте, что Mathematica сама поняла, что разложение нужно выполнять в кольце целых гауссовых чисел. Но как разложить на простые множители в кольце целых гауссовых чисел натуральные числа? Ведь, например, FactorInteger[41] = {{41,1)}.
В подобных случаях, т.е. когда в качестве аргумента функции FactorInteger выступает рациональное вещественное число, а разложить аргумент нужно на простые гауссовы числа, область разложения нужно указать явно. Для этого необходимо с помощью второго аргумента функции FactorInteger установить опцию Gaussianlntegers равной True. Вот несколько примеров, в которых показано, как это делается.
Factorlnteger[41,GaussianIntegers->True]={{-1,1},{4+5i,l},{5+4i,lH
FactorInteger[5,GaussianIntegers->True]={{-i,l},{!+2i,i},{2+i,1}}
Factorlnteger[2,GaussianIntegers->True]={{-i,1},{1 + i,2}}
Factorlnteger[11,GaussianIntegers->True]={{11,1}}
FactorInteger[13,GaussianIntegers->True]={{-i,l},{2+3i,l},{3+2
i,l}}
Как видите, ничего сложного!
Факторизация очень больших чисел
Как мы уже видели, функция Factorlnteger вполне справляется с разложением чисел, десятичная запись которых содержит не более 60—70 десятичных знаков (это примерно две сотни двоичных). Хотя именно такие числа чаще всего встречаются на практике, их множество конечно. Дополнение же этого множества до множества
натуральных чисел бесконечно! Поэтому иногда приходится раскладывать и числа, содержащие несколько сотен, а то и тысяч десятичных знаков. Конечно, в таких случаях зачастую приходится полагаться на удачу. Однако и здесь может помочь Mathematica. Например, если известно, что некоторое число является большой степенью некоторого основания, то достаточно разложить только основание. Так что этот случай большого числа для процедуры факторизации можно считать тривиальным. Несколько менее тривиальным является случай факториала.
Факторизация факториалов
Факториалы являются классическим примером больших чисел. В школе, примерно класса с шестого, учителя плавно готовят детей к тому, что факториалы очень быстро растут, а при изучении комбинаторики говорят, что уже 8! = 40320. Тех же, кто этого не устрашится, на школьном кружке пугают тем, что 100! — невообразимо большое число. Такое большое, что даже вычислить его немыслимо. (Но члены школьного математического кружка обычно знают, что это число вычислил Мольтерер еще до появления ЭВМ.) Дня тех же, кто не убоялся этого числа и (зачастую вопреки устрашениям учителей) преодолел конкурсный отбор в вузы, у профессоров есть очередная страшилка: 1000!. Что-то я не видел профессора, который бы выписал десятичную запись этого числа на доске! Наверное, для профессоров оно и вправду страшное! Но не для нас. Мы его (вместе с системой Mathematica) выпишем раньше, чем профессор успеет моргнуть оком.

Действительно, число огромное! Правда, факторизовать его совсем несложно, так как его простые делители известны: даже пятиклассник без труда сообразит, что ими будут все простые числа, меньшие
n = 1000. Что же касается определения показателей, с которыми они входят в каноническое разложение, то здесь положение более сложное. Обычно пятикласснику (участнику городской или районной олимпиады по математике) нужно от пяти до десяти минут на вывод и проверку необходимой формулы. Но ведь Mathematica (точнее, функция
FactorInteger) не проверяет, является ли каждое предлагаемое ей число факториалом некоторого другого числа, и потому применить формулу не сможет! Так сколько же ей понадобится времени на факторизацию этого монстра? На самом деле ответ получается в мгновение ока.
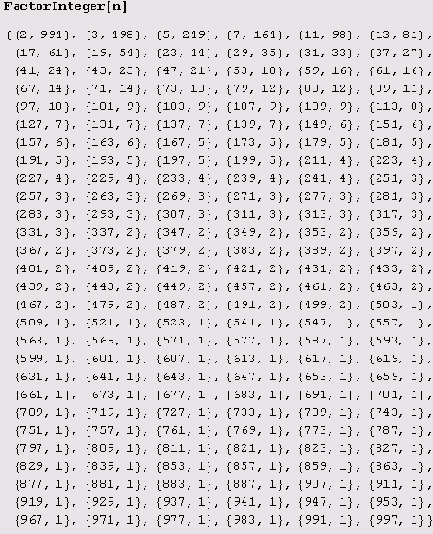
Почему же тогда это разложение получается так быстро? Тому есть две причины. Во-первых, функция Factorlnteger реализует довольно хитрый алгоритм (и к тому же усовершенствованный в версии 5), который умеет пользоваться особенностями числа и ранее найденными множителями. Во-вторых, число имеет малые простые делители, притом в достаточно больших степенях (взгляните на разложение и убедитесь в этом самостоятельно). Поэтому уже в самом начале, как только найден очередной небольшой простой делитель, число делится на его достаточно большую степень, и поиск следующего делителя выполняется для уже значительно меньшего числа. Например, когда найдены все простые делители, меньшие 500, остается факторизовать число
15691 53857 18474 74009 83807 62903 18629
41145 72096 17012 19604 99858
85055 99420 28601 60316 94401 22137 22852
86216 37326 13501 59916 38173
00885 96291 76502 03413 58819 32577 52694 92805
54593 08494 87900 72440 14847 75831
74209 25608 64073 74119.
А ведь это число существенно меньше первоначального. К тому же его простые делители также являются последовательными простыми числами. И потому, хотя уже и не так стремительно, но подлежащее факторизации число все время уменьшается. А это значит, что не приходится испытывать числа, большие 1000. Добавьте сюда еще одну техническую деталь: работать приходится с все более короткими числами, и вы поймете, почему процесс заканчивается столь быстро.
Но есть огромное множество гораздо меньших чисел (вроде 1001-1, (1079-1)/9 и т.д.), которым повезло гораздо меньше. Быстро разложить их функция Factorlnteger не может. Как же быть?
Функция FactorIntegerECM: попытка факторизации больших чисел Мерсенна
Давайте на примере попытки разложения больших чисел Мерсенна рассмотрим,
как Mathematica позволяет приблизиться к решению задачи факторизации очень больших чисел.
Факторизация 317-го числа Мерсенна М317
Конечно, можно попытаться применить функцию Factorlnteger. Но это не даст результата (за приемлемое время). Можно, правда, "попросить" функцию Factorlnteger найти хоть какие-нибудь делители числа Мерсенна
М317. Для этого нужно воспользоваться опцией FactorComplete->False.
FactorInteger[M317-1,FactorComplete->False]
Результат будет таким.
FactorInteger::facfn: Unable to factor 28072587476617 «64» 65592773657961.
More...
Чуть ниже будут и найденные множители.
{{9511, 1), {280725874766179960361032187226573
45634038278340298769450465
797600439224658035965592773657961,1}}
Хорошо, конечно, что нашли множитель 9511, но вот второй множитель... Неизвестно, даже простой ли он. Можно, конечно, попытаться повторить процедуру для него, но это ни к чему новому не приведет.
Factorlnteger::facfn:
Unable to factor 28072587476617
«64» 65592773657961. More...
{{2807258747661799603610
321872265734563403827834
0298769450465797600439
224658035965592773657961,1}}
В этом случае все придется сделать вручную:.. Возможно, вы подумали о формулах сокращенного умножения. Да, действительно, часто они помогают. (Мы в этом уже не раз убеждались.) Но в данном случае 317 — простое число (я специально так подобрал индекс числа Мерсенна), и применить формулы сокращенного умножения просто так, "в лоб", не удастся. Придется использовать другую функцию. Она есть в пакете теории чисел, который загружается так: «NumberTheory' FactorlntegerECM'.
Сама функция называется FactorIntegerECM. Ее первоначальный алгоритм придумал X. Ленстра (Н. W. Lenstra) в 1985 году. В нем используется теория эллиптических кривых. Функция FactorIntegerECM очень эффективна там, где FactorInteger не справляется. Правда, с другой стороны, она не столь услужлива, как FactorInteger. Она находит только один множитель, притом не обязательно простой. К тому же она привередлива: ее поведение не предсказуемо, если в качестве аргумента передать ей простое число. Поэтому предварительно нужно проверить, что аргумент не является простым числом. Это делается с помощью функции PrimeQ.
Давайте теперь попытаемся применить функцию FactorIntegerECM для какого-нибудь небольшого числа, например 91. (Это число, как мы знаем, не простое.)
FactorIntegerECM[91 ]
А вот и результат.
13
Да, найден только один множитель... Остальное приходится делать вручную. Рассмотрим теперь более сложный пример.
m=12
n = Prime[10Am] Prime[10Лт+1]
Вот что получилось:
12 899773470806612917304808883
Теперь давайте разложим п (оно составное, так как является произведением двух последовательных достаточно больших простых чисел).
FactorIntegerECM[n]
И вот один из сомножителей: 29996224275851
Вот еще один пример применения функции FactorIntegerECM.
n=(2^58 - 27) * (2^127 - 1) 4903985730770843887365 5151436140637119954221204852703259
Теперь ищем какой-нибудь делитель этого числа.
288230376151711717
Наконец, освоившись с функцией FactorIntegerECM на этих более или менее простых примерах, можем попытаться применить ее к факторизации числа Мерсенна Мт. Как мы помним, оно имеет делитель 9511. Сначала убедимся, что он простой.
PrimeQ[9511] True
Теперь можем разделить на него число Мерсенна М317.
n=(2Л317-1)/9511
28072587476617996036103218722657345
63403827834029876945046579760043922
4658035965592773657961
После этого нужно убедиться, что это число составное.
PrimeQ[n] False
Значит, можно применить функцию FactorIntegerECM.
m=Factor!ntegerECM[n]
Через 205,375 с (процессор Pentium 2,4 ГГц) получаем один из его делителей:
587492521482839879 Он простой.
PrimeQ[m] True
Поэтому можем заниматься только частным n = n/m.
n=n/m
477837358776284792683873587315
9342707436119775645430680034874628800586
6959
Опять нужно проверить, простое ли оно.
PrimeQ[n]
Эта проверка занимает всего лишь 0,016 с, и оказывается, что оно составное.
False
Значит, можем снова применить функцию FactorIntegerECM.
m=Factor!ntegerECM[n]
На этот раз понадобится 727,047 с, чтобы найти очередной делитель. 4868122671322098041565641
Снова нужно проверить, прост ли найденный делитель. PrimeQ[m]
Эта проверка выполняется пoчти мгновенно, и оказывается, что делитель действительно прост.
True
Значит, снова можем заниматься только частным n= n/m.
n=n/m 9815639231755686605031317440031161584572466128599
Опять нужно проверить, простое ли оно.
PrimeQn]
Эта проверка занимает всего лишь 0,015 с, и оказывается, что найденное частное является простым числом.
PrimeQ[ n] True
Таким образом, мы нашли все простые множители 317-го числа Мерсенна М317 и тем самым разложили этого числового великана на простые множители.
М317 = 9511X587492521482839879X486812267
1322098041565641X981563923175568
6605031317440031161584572466128599
Факторизация 337-го числа Мерсенна М337
Чтобы освоить методику применения функций Factorlnteger и FactorIntegerECM, попробуем разложить на простые множители 337-е число Мерсенна M337. Сначала можно попытаться применить функцию Factorlnteger. Но как и в случае 317-го числа Мерсенна M317, это не даст результата за приемлемое время. Тогда применим функцию Factorlnteger с опцией FactorComplete->False, чтобы найти хоть какие-нибудь делители 337-го числа Мерсенна М337.
Factorlnteger[2^337-1,FactorComplete->False]
Результат будет таким.
Factorlnteger::facfn: Unable to factor
57238939242563 «51» 465444456568561. More...
Зато чуть ниже будут найдены делители.
{{18199, 1}, (2806537,1), (95763203297, 1},
{572389392425637497118853974356
80799950268490508661316904465621201465444456568561, 1}}
Иными словами,
М337=18199X2806537X95763203297X572389392425637
497118853974356807999502
68490508661316904465621201465444456568561
Теперь нужно проверить, просты ли найденные делители.
PrimeQ[18199] True
PrimeQ[2806537] True
PrimeQ[95763203297] True
PrimeQ[5723893924256374971188539743568079
99502684905086613169044656212
01465444456565-61] False
Как видите, все они, за исключением последнего (обозначим его временно через n), самого большого, простые. (Все это заняло менее двух секунд.)
Поскольку 337 — простое число (я опять специально подобрал индекс числа Мерсенна), формулы сокращенного умножения "в лоб" применить не удастся. Но ведь мы можем загрузить пакет теории чисел.
<<NumberTheory"FactorIntegerECM`
Теперь, когда пакет загружен, можно вызвать функцию FactorIntegerECM.
FactorIntegerECM[572389392425637497118
85397435680799950268490508661316 90446562120146544445656561]
Мгновенно находится множитель.
726584894969
Давайте проверим, прост ли он.
PrimeQ[726584894969]
True
Оказывается, прост. Поэтому разделим на найденный множитель полученное на предыдущем шаге число, присвоим частное переменной п и проверим, является ли частное простым числом.
n=57238939242563749711885397435680799950268490
508661316904465621201465
44445656561/726584894969
787780473264667429936124208424161983
11394008068822475527239136925369
PrimeQ[n] True
Поскольку полученное частное является простым числом, мы нашли все простые множители 337-го числа Мерсенна М337 и тем самым разложили и этого числового великана на простые множители.
М337=18199x2806537x95763203297x
726584894969x787780473264667429
93612420 842416198311394008068822475527239136925369
Функция FactorIntegerECM: поиск делителей 5011 -го числа Мерсенна М5011
Функция FactorlntegerECM иногда может находить делители таких чисел, которые можно смело отнести к разряду супервеликанов. Еще в середине прошлого столетия было известно, что 5011-е число Мерсенна Мхи — составное. Вот этот супервеликан.

С помощью системы Mathematica можно почти мгновенно убедиться, что это число составное.
PrimeQ[M5011] False Однако неплохо было бы найти хотя бы какой-нибудь его делитель.
m=FactorIntegerECM[M5011]
Системе Mathematica потребуется менее 36 секунд, чтобы найти делитель m = 80177. Теперь проверим, прост ли найденный делитель.
PrimeQ[m] True
Оказывается, да! Есть шансы разложить 5011-е число Мерсенна M5011 на простые множители? Давайте попытаемся. Для этого разделим 5011-е число Мерсенна Мт] на найденный делитель.

Но простое ли число nl Давайте проверим.
PrimeQ[n] False
Нет. В таком случае к нему можно применить функцию FactorIntegerECM. Но на этот раз результата не дождаться даже за несколько часов... Конечно же, функция FactorIntegerECM чрезвычайно эффективна, но всех проблем теории чисел она решить не может...
Функция FactorIntegerECM: поиск делителей М13 -го числа Мерсенна М8191= М13
Но все же ситуация не столь безнадежна. Некоторые специалисты по теории чисел, например, долгое время считали, что если число Мерсенна Mn, является простым, то и число МMn тоже простое. Это действительно так для четырех наименьших простых чисел Мерсенна. Но лишь в 1953 году Д. Ю. Уиллер показал, что для пятого простого числа Мерсенна это не так. Пятое простое число Мерсенна М13 = 8191, однако число A/W], имеющее 2466 цифр, является составным. Тем не менее в течение более чем десятилетия после .открытия Уиллера не удалось найти ни одного его простого делителя. С помощью функции FactorIntegerECM это можно сделать за считанные минуты (само число Мм в распечатке опущено).
ММ13=2^8191-1
m=FactorIntegerECM[MM13]
338193759479
С другой стороны, давно было известно, что М17и M19 — простые числа. Кроме того, еще в 1957 году было доказано, что MM17 делится на n1 = 1768(2'7-1)+1 = 231733529, а ММn — на n2= 120(2|9-1)+1 =62914441. Тем не менее функция FactorIntegerECM, не говоря уже о функции FactorInteger, не может обнаружить ни одного нетривиального делителя МM17 или MM19 . Интеллект человека сильнее. Мораль: Хотя всех проблем теории чисел решить не может даже функция FactorlntegerECM, воспринимать это следует без излишнего пессимизма...
Для нахождения канонического разложения целых
Для нахождения канонического разложения целых чисел, дробей и целых гауссовых чисел лучше всего подходит функция Factor-Integer. Она возвращает список пар простых делителей и их показателей, а также, при необходимости, делитель единицы, указывающий знак или позволяющий сгруппировать сопряженные множители. При этом сорока-, а то и шестидесятиразрядные числа разлагаются практически сразу. Среди же семидесяти- и восьмидесятиразрядных чисел велика вероятность встретить число, (растеризовать которое за приемлемое время не удается. (Двоичное представление таких чисел содержит более двух сотен цифр.) Во всяком случае, не стоит пытаться делать это в цикле, если в нем не предусмотрены какие-либо средства оповещения о ходе выполнения процесса факторизации. Конечно, в отдельных случаях могут быть успешно разложены и числа, десятичная запись которых содержит и несколько десятков тысяч цифр. Обычно это степени или произведения степеней относительно небольших простых чисел. К этой категории можно отнести, например, факториалы.
Если же функция FactorInteger со своей работой за приемлемое время не справляется, можно сначала найти только те делители, нахождение которых не составит труда для нее, — именно для этого предназначена опция FactorComplete->False. Все же чаще приходится прибегать к имеющейся в пакете теории чисел функции FactorIntegerECM. Однако эта функция за один раз находит только один делитель, притом не обязательно простой. Кроме того, она может зациклиться, если в качестве аргумента получит простое число. Так что перед вызовом этой функции нужно проверить, не является ли ее аргумент простым числом — это делается с помощью функции PrimeQ. (Как правило, функция PrimeQ работает очень быстро.) Получив очередной делитель, число можно разделить на него и проверить, не является ли частное простым числом. Если частное окажется простым числом, то фактически каноническое разложение можно считать полученным, если известны канонические разложения найденных ранее делителей. Если же частное или какой-нибудь делитель окажется числом составным, к нему можно попытаться снова применить функцию FactorIntegerECM. Повторяя эту процедуру достаточное число раз, иногда (для относительно небольших великанов часто) удается найти каноническое разложение.
Если же и этот метод не приводит к успеху, помочь могут различные формулы (например, разложения суммы или разности степеней и т.п.) и предварительно составленные таблицы. Благодаря системе Mathematica к таблицам приходится прибегать существенно реже, чем в докомпьютерную эпоху. Более того, сами таблицы можно составить с помощью программ, написанных на языке программирования, встроенном в систему Mathematica. Однако, как и в эпоху Эйлера и Гаусса, таблицы незаменимы при поиске нетривиальных закономерностей в канонических разложениях чисел того или иного вида. Однако представление, возвращаемое функцией Factorlnteger, несколько "однолинейно" и потому удобно скорее для дальнейшего использования в качестве аргумента других функций, чем для чтения человеком. Хотя это представление система Mathematica может преобразовать в различные форматы, подчас проще написать макрос, преобразующий его в привычный вид.