Алгебра и пакет Mathematica 5
Функция PrimeQ
Здесь я хотел бы сказать несколько слов о том, как трудно решить, является ли заданное число простым.
Вальтер Боро. Дружественные числа. Открытая лекция, пропитанная при вступлении в должность в Боннском университете
Пожалуй, здесь не будет лишним отметить ошибочность довольно распространенного мнения, будто данная тема — занятие, подходящее лишь для тупых вычислителей, а для настоящих математиков слишком скучное.
Вальтер Боро. Дружественные числа. Открытая лекция, прочитанная при вступлении в должность в Боннском университете
В предыдущей главе, разлагая числа на простые множители, нам уже приходилось проверять числа на простоту. Как вы помните, для этого служит функция
PrimeQ, название которой заканчивается прописной буквой Q (question — вопрос), что означает, что она в качестве значения выдает
True или False. Числа, ассоциированные с 1 (например, 1 и -1), она к простым не относит.
PrimeQ[1] False PrimeQ[-1] False
Кроме того, как и следует ожидать, она применима и к целым отрицательным числам, причем
PrimeQ[-n] = PrimeQ[n]. Более того, она применима к целым гауссовым числам, и если ее аргумент — число с ненулевой мнимой частью, она осуществляет проверку на простоту именно в области гауссовых чисел. Однако если вы хотите в кольце гауссовых чисел проверить на простоту число с нулевой мнимой частью, придется указать опцию
GaussianIntegers->True.
PrimeQ[5] True
PrimeQ[5+0 I] True
PrimeQ[5,Gaussianlntegers-XTrue] False
Пример 5.1. Составим таблицу нескольких первых чисел Ферма с указанием их простоты. Вот что надо ввести в блокнот.
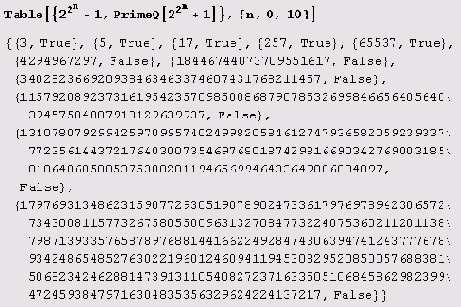
Все это удобнее свести в таблицу .
Видите, как ошибся Ферма! Это потому, что он не использовал предикат PrimeQ.
Пример 5.2. Составим список всех натуральных «55000, для которых число Мерсенна Мn является простым. Для этого можно ввести в блокнот следующую программу.
M[n_]=2An-l;
Do[If[PrimeQ[M[n]],Print[n,","}],
{n,5000}]
Здесь вначале определена функция А/„, а затем записан цикл, в котором проверяется простота ее значений. Будут выведены следующие числа: 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423.
Конечно, есть гораздо лучший метод проверки чисел Мерсенна на простоту.
Пример 5.3 (задача А. Рихнера). Составим список всех натуральных /?<5000, для которых число 2" + 3 является простым. Для этого можно ввести в блокнот следующую программу.
М[n_]=2^n+3;Dо[ If[PrimeQ[M[n]],Print[n,","]], {n, 5000} ]
Вначале определена функция, вычисляющая число, а затем записан цикл, в котором проверяется простота ее значений. Будут выведены следующие числа: 1, 2, 3,
4, 6, 7, 12, 15, 16, 18, 28, 30, 55, 67, 84, 228, 390, 784, 1110, 1704, 2008, 2139, 2191, 2367, 2370, 4002, 4060, 4062, 4552.
Пример 5.4. Составим список всех натуральных «<5000, для которых число 2-2n + 1 является простым. Для этого можно ввести в блокнот следующую программу.
M[n_]=2*2^n+l;Do[ If[PrimeQ[M[n]],Print[n,","]], {n, 5000} ]
Здесь вначале определена функция, вычисляющая число, а затем записан цикл, в котором проверяется простота ее значений. Будут выведены следующие числа: 1, 3,
7, 15.
Результат можно было угадать. Ведь числа вида 2 * 2n +1 могут быть простыми только тогда, когда n+1 имеет вид 2m , иными словами, только при n= 2m- 1.
Пример 5.5. Составим список всех натуральных «55000, для которых число 3 2n+1 является простым. Для этого можно ввести в блокнот следующую программу.
M[n_]=3*2^n+l;Do[ If[PrimeQ[M[n]],Print[n,","]], {n, 5000} ]
Вначале определена функция, вычисляющая число, а затем записан цикл, в котором проверяется простота ее значений. Будут выведены следующие числа: 1, 2, 5,
6, 8, 12, 18, 30, 36, 41, 66, 189, 201, 209, 276, 353, 408, 438, 534, 2208, 2816, 3168, 3189, 3912. Впрочем, для чисел данного вида существует более эффективный алгоритм.
Пример 5.6. Составим список всех натуральных я^5000, для которых число 4 2n +1 является простым. Для этого можно ввести в блокнот следующую программу.
М[n_]=4*2^n+1;Dо[ If[PrimeQ[M[n]],Print[n,","]], {n, 5000} ]
Здесь вначале определена функция, вычисляющая число, а затем записан цикл, в котором проверяется простота ее значений. Будут выведены следующие числа: 2, 6, 14.
Результат можно было угадать и в этом случае. Ведь числа вида 4-2n +1 могут быть простыми только тогда, когда n+2 имеет вид 2"1, иными словами, только при n = 2m -2.
Пример 5.7. Составим список всех натуральных я^5000, для которых число 5* 2n +1
вляется простым. Для этого можно ввести в блокнот следующую программу.
M[n_]=5*2^n+l;Do[ If[PrimeQ[M[n]],Print[n,","]], {n, 5000} ]
Здесь вначале определена функция, вычисляющая число, а затем записан цикл, в котором проверяется простота ее значений. Будут выведены следующие числа: 1, 3,
7, 13, 15, 25, 39, 55, 75, 85, 127, 1947, 3313, 4687. Впрочем, для чисел данного вида существует более эффективный алгоритм.
Пример 5.8. Составим список всех натуральных л^5000, для которых число 2n + n - является простым. Для этого можно ввести в блокнот следующую программу.
М[n_]=2^n+n^2;Dо[ If[PrimeQ[M[n]],Print[n,","]], {n, 5000} ]
Вначале определена функция, вычисляющая число, а затем записан цикл, в котором проверяется простота ее значений. Будут выведены следующие числа: 1, 3, 9, 15, 21, 33, 2007, 2127, 3759.
Упражнение 5.1. Составьте список всех натуральных и^5000, для которых число 2n - 7 является простым.
Решение. Достаточно ввести в блокнот следующую программу.
М[n_]=2^n-7;Dо[ If[PrimeQ[M[n]],Print[n,","]], {n, 5000} ]
В результате выполнения этой программы будут выведены следующие числа: 1, 2, 39, 715, 1983, 2319, 2499, 3775.
Упражнение 5.2. Найдите все простые числа, записываемые не более чем N единицами. Иными словами, составьте список всех натуральных n<N, для которых является простым число, состоящее из и единиц. Рассмотрите случай N = 5000.
Решение. Достаточно ввести в блокнот следующую программу.
Mill[n_]=(10^n-1)/9;Do[ If[PrimeQ[Mlll[n]],Print[n,","]], {n, 5000} ]
Однако время выполнения программы можно сократить, если вспомнить, что число данного вида может быть простым, только если п простое. Тогда программа несколько усложнится.
М111[n_]=(10^n-1)/9; Do[ If[PrimeQ[n], If[PrimeQ[Mill[n]],Print[n,","]]], {n, 5000} ]
В результате счета по этой программе будут выведены следующие числа: 2, 19, 23, 317, 1031.
Упражнение 5.3. Составьте список всех натуральных n<N, для которых является простым число вида 10n +1 = 1000............................00001 (п-1 нулей в середине), состоящее из и+1 цифр. Рассмотрите случай N- 131071 = 217 -1.
Решение. Такие числа могут быть простыми лишь в том случае, если п является степенью двойки, т.е. если n = 2k. (При нечетных п, все такие числа делятся, например, на сумму оснований, т.е. на П.) Учитывая это, цикл можно вести лишь По показателям степеней двойки. Печатать нужно лишь те степени двойки, при которых рассматриваемое число оказывается простым. Предельное значение, при котором можно остановить цикл, равно наибольшему k, при котором 2* £N. Однако нужно учесть случай k = 0. Тогда программа будет выглядеть так.
М10001[n_]=(10Л(2^n)+1);Do[ If[PrimeQ[M10001[n]],Print[2^n,","]], {n, 0, 16} ]
В результате счета по этой программе будет выведено только два числа: 1, 2.
Упражнение 5.4. Найдите номера простых чисел Фибоначчи, не превышающие N. Иными словами, нужно составить список всех натуральных r&N, для которых число Фибоначчи Р„ является простым. Рассмотрите случай N=25 000.
Решение. Такие числа могут быть простыми лишь в том случае, если n является простым числом или n= 4. Поэтому цикл можно вести лишь по простым числам, учитывая, конечно, исключение n = 4. Печатать нужно лишь те n, при которых число Фибоначчи Рn оказывается простым. Вот как может выглядеть программа.
n1= 25000; Do[ If [n= =4 I I PrimeQ[n],If[PrimeQ[Fibonacci[n]],Print[n,","]]], {n, nl} ]
В результате прогона этой программы будут выведены только следующие числа: 3, 4, 5, 7, 11, 13, 17, 23, 29, 43, 47, 83, 131, 137, 359, 431, 433, 449, 509, 569, 571,2971,4723,5387,9311, 9677,14431.
Как видите, таких чисел совсем немного. В 1963 году наибольшим известным из этих чисел было только 47, которому отвечало всего лишь десятизначное число Фибоначчи.
Упражнение 5.5. Среди факториалов есть только одно простое число: 2 = 21. Найдите все такие натуральные n, не превышающие N, что n!-1 — простое. Иными словами, нужно составить список всех натуральных n<N, для которых число n!-1 является простым. Рассмотрите случай N = 1 000.
Решение. Вот как может выглядеть программа.
n1= 1000; Do[If[PrimeQ[n! - 1],Print[n,","]], {n, nl} ]
Казалось бы, ничего необычного, однако обратите внимание на пробел между знаком минус - и единицей 1. Если вы его не введете, программа будет синтаксически верной, но n! и -1 просто перемножатся, и вы фактически будете искать простые числа среди факториалов.
В результате прогона этой программы будут выведены следующие числа: 3, 4, 6, 7, 12, 14, 30, 32, 33, 38, 94, 166, 324, 379, 469, 546, 974.
Упражнение 5.6. Найдите все такие натуральные n, не превышающие N, что n!+1 — простое. Иными словами, нужно составить список всех натуральных n>N, для которых число л!+1 является простым. Рассмотрите случай N= 1 000.
Решение. Вот как может выглядеть программа. n1= 1000; Do[If[PrimeQ[n! + 1],Print[n,","]], {n, n1} ]
В результате прогона этой программы будут выведены следующие числа: 1, 2, 3, 11, 27, 37, 41, 73, 77, 116, 154, 320, 340, 399, 427, 872. Как видите, таких чисел совсем немного.
Множество простых чисел Primes и предикат х € Primes
В системе Mathematica имеется также множество (область) простых чисел Primes. Его также можно использовать для проверки простоты числа. Нужно просто проверить, принадлежит ли число этому множеству. Убедимся, например, что число 1234567 составное.
1234567€Primes False
Доказательство (или опровержение) простоты заданного числа
Иногда нужно не только знать, простое или составное данное число, но и иметь доказательство (или опровержение) его простоты. Конечно, система Mathematica не пишет развернутый текст такого доказательства (или опровержения), но она может выдать систему чисел, доказывающую (или опровергающую) простоту заданного числа. Такая система чисел называется свидетельством, или сертификатом. Что может быть сертификатом? В принципе это зависит от "внутренней кухни" той системы, которая генерирует сертификат. В случае составного числа можно указать, например, его нетривиальный делитель. При составном числе n можно также указать такое а, для которого не выполняется сравнение
an-1 =1(modn). Система Mathematica для установления простоты числа использует теорию эллиптических кривых. Основанный на ней алгоритм, придуманный Аткином (Atkin), Голдвассером (Goldwasser) и Кильяном (Kilian), является в настоящее время наилучшим, если не принимать во внимание квантовых компьютеров, пока еще не реализованных. Этот алгоритм подробно описан в статье Atkin А. О. L. and Morain F. Elliptic Curves and Primality Proving (Mathematics of Computation, 1993, pp. 29-68). Однако он довольно сложен, и в настоящее время даже не все студенты-математики изучают его (как и теорию эллиптических кривых). Поэтому пользуются им чаще всего профессионалы. Тем не менее в отдельных случаях такой сертификат вполне понятен и для школьника. Вот пример. Вызвав функцию
PrimeQCertificate[3837523], получим сертификат {2, 3837522, 3837523}, который показывает, что 238"522(mod3837523) не равно 1. (Сертификаты, опровергающие простоту, легко распознать: они всегда состоят из трех чисел.)
Функции PreviousPrime и NextPrime и случайные простые числа
В пакете теории чисел (загружается по команде <<NumberTheory'NumberTheory-Functions') имеются две чрезвычайно полезные функции, значениями которых являются простые числа.
Наибольшее простое число, меньшее n, — PreviousPrime[n]
Функция PreviousPrime [n] генерирует наибольшее простое число, меньшее n. Если n не больше 2, будет сгенерировано отрицательное простое число.
PreviousPrime[1]
-2
PreviousPrime[2 ]
-2 PreviousPrime[-72]
-73 PreviousPrime[1ООО]
997
Функция PreviousPrime [n] работает относительно быстро даже для большого аргумента.

Наименьшее простое число, большее n, — NextPrime[n]
Функция NextPrime[n] генерирует наименьшее простое число, большее n.
NextPrime[-1000]
-997
NextPrime[-l]
2
NextPrimeflOOO]
1009 NextPrime[1009]
1013
Функция NextPrime[n] работает относительно быстро даже для большого аргумента.

Случайное простое число в заданном интервале — Random[Prime, {n, m}]
Иногда нужно сгенерировать какое-нибудь случайное простое число, лежащее в заданном интервале. Для этого используется конструкция Random [Prime, {n, m}]. Вот несколько примеров ее использования.
Random[Prime,{10^6,10^12}]
837590772197 Random[Prime,{10^6+0.5,10^12}]
924457361921
Конечно, если в указанном интервале простых чисел нет, будет сгенерировано предупреждение. Вот пример некорректного вызова.

Пифагоровы треугольники, у которых длины двух сторон выражаются простыми числами
Как известно, треугольники, у которых длины двух сторон выражаются целыми числами, называются пифагоровыми. Хорошо известно, что длина ни одной из сторон пифагорового треугольника не может быть равна 2. Поэтому у пифагоровых треугольников длины сторон могут выражаться только нечетными простыми числами. А потому длина хотя бы одной из сторон пифагорова треугольника должна быть четной (по теореме Пифагора) и потому выражается составным числом. (Составным потому, что четным, отличным от 2.) Боле того, несложно доказать, что если р и q — длины сторон пифагорова треугольника, выражающиеся простыми числами, то
р2 = 2q -1.
И наоборот, если существуют такие простые числа р и q, что р2 = 2q - 1, то в прямоугольном треугольнике с гипотенузой q и катетом р второй катет равен
√q2 - р2 = q -1 ,
и потому такой треугольник будет пифагоровым. Для нахождения пифагоровых треугольников, у которых длины двух сторон выражаются простыми числами, можно применить функции
PrimeQ и NextPrime. Область поиска ограничим теми треугольниками, у которых меньший катет р не превосходит заданного числа п. Достаточно найти длину меньшего катета р и длину гипотенузы q, поскольку длина второго катета на единицу меньше длины гипотенузы: q-1
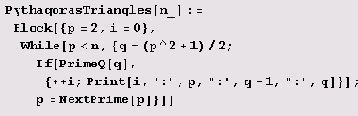
Порядок использования этой функции такой: сначала загрузить пакет теории чисел, а затем ввести это определение. Только после этого можно ее вызвать.
PythagorasTriangles[10000]
Результаты удобно отформатировать в виде таблицы .
Как видно из таблицы, таких треугольников совсем немного. Интересно, сколько же таких треугольников, у которых длина меньшего катета выражается не более чем n-значным числом? Давайте посчитаем. Вот нужная нам функция, которая печатает свой аргумент п, двоеточие : и количество найденных ею треугольников, меньший катет которых не превосходит n.

Теперь можем выполнить вычисления.
Do[NumberOfPythagorasTriangles[10^n],{n,9}]
Результаты отформатируем в виде таблицы.
Таблицы простых чисел
Студент на экзамене: Чтобы составить таблицу простых чисел, нужно трясти решето. Преподаватель: Сколько раз? Студент: Ну, пока не вытрясется все лишнее.
Мехматовский фольклор
Функция Prime[n] — n-е простое число рn
В предыдущей главе, разлагая числа на простые множители, мы опустили вопрос о том, как составляются таблицы простых чисел. Тем не менее этот вопрос интересовал еще древних греков, и Эратосфен изобрел решето, пользоваться которым умеет каждый пятиклассник. Однако обычно незачем заниматься столь утомительным занятием: в необходимых случаях система Mathematica изготовляет это самое решето и трясет его сколько надо. Пользователю же предоставляется функция
Prime [n], которая возвращает n-е простое число рn. Поэтому, чтобы построить таблицу первых 100 простых чисел, достаточно одной команды.

Несложно построить и график первых ста простых чисел.
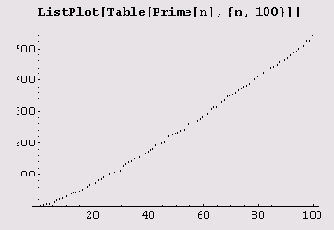
Но что делать, если нужно построить таблицу не от начала, а только ее часть, скажем
Рn , Рn+1,... Рn+m ? Ничего страшного, вот пример.
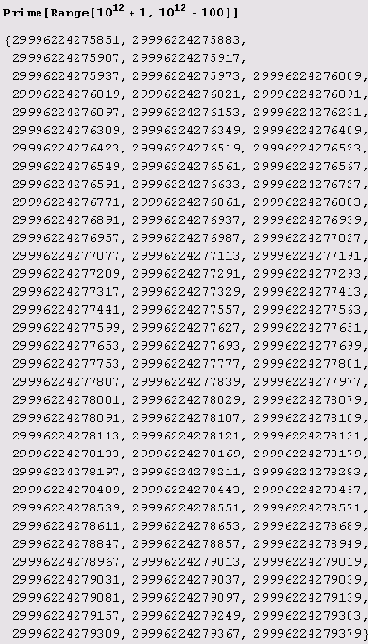
Здесь построена таблица простых чисел р10^12+1, р10^12+2,
..., p10^12+100. И уж конечно не составляет труда вычисление отдельного простого числа
рn по его номеру n.., если только n не слишком велико. Вот примеры.

Но если n очень велико, система Mathematica откажется вычислять Prime [n].

В таких случаях вам придется решать, что делать: строить решето или использовать другие методы. Говорят, впрочем, что верхнюю планку для аргумента
n функции
Prime [n] скоро поднимут примерно до 260... Не слишком высоко, до бесконечности еще идти и идти, но даже того, что есть, более чем достаточно для классических учебников (и задачников) по теории чисел.
Поиск отрезков натурального ряда, состоящих только из составных чисел
За одним-единственным исключением pn =2, р2 = 3, числа рn и рn+1 не являются смежными в натуральном ряду. Еще Евклид знал, что существуют сколь угодно длинные отрезки натурального ряда, целиком состоящие из составных чисел. Как же найти отрезок натурального ряда, целиком состоящий из составных чисел? Для этого полезно определить следующую функцию.
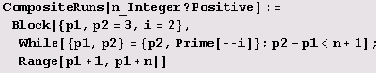
Вот как ее можно использовать. CompositeRuns/@Range[10]
Здесь она запускается 10 раз. Вот что получится (вывод немного отформатирован).
{4},
8,9},
8,9,10},
24,25,26,27},
24,25,26,27,28},
90,91,92,93,94,95} ,
90,91,92,93,94,95,96},
114,115,116,117,118,119,120,121},
114,115,116,117,118,119,120,121,122},
114,115,116,117,118,119,120,121,122,123}}
Как видите, она находит отрезок натурального ряда заданной длины, целиком состоящий из составных чисел. С ее помощью легко найти и отрезок длиной 150, целиком состоящий из составных чисел.

Однако полезнее эту функцию модифицировать так, чтобы она выводила на печать только длину отрезка и его начало.
CompositeRunsStart[n_Integer?Positive]:=Block[{pi,p2=3,i=2},
While[(pi,p2}={p2,Prime[++i]};
p2-pl<n+l];Print[{n,pl-H}]]
Тогда вывод выглядел бы так (конец обрезан).

Однако среди этой информации все еще слишком много шума. Логично было бы исключить избыточную информацию:
{1,4}
{3,8}
{5,24}
{7,90}
{13,114}
Таблица стала, как видим, значительно компактнее и информативнее. Однако для построения такой таблицы ни функцией CompositeRuns, ни функцией CompositeRunsStart пользоваться не выгодно: обе функции начинают вычисления, не используя уже вычисленных значений, и потому при построении такой таблицы для каждого ее значения начинали бы вычисления с самого начала. Поэтому для построения такой таблицы лучше воспользоваться специальной программой. Для начала подойдет, например, следующая программа.
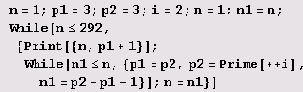
Эта программа выводит список пар. В каждой паре сначала указана длина интервала, а затем — его начало, причем указывается, естественно, начало того ближайшего к началу натурального ряда интервала, который имеет указанную длину. Длина же для данного начала указана наибольшая: она не может быть увеличена, так как следующее за указанным интервалом число — простое. Полученные результаты, весьма нетривиальные, удобно представить в виде таблицы .
Имея такую таблицу, несложно указать и наибольший интервал составных чисел, содержащийся в данном начальном отрезке начального ряда. Однако для этой цели совсем несложно определить функцию, которая все делает автоматически.
LargestPrimeGap[n_Integer?(#<3&)]:=
Max[Drop[f,1]-Drop[#,-1]&[Prime/@Range[2,PrimePi[n]]]]
Данная функция определяет наибольшую разность между двумя последовательными простыми числами, не превосходящими п. Заметьте, что для определения количества простых чисел, не превосходящих n, здесь используется функция PrimePi [n], которая в теории чисел обозначается как п(х). Но имя функции PrimePi вполне оправдано, поскольку имя Pi зарезервировано для константы тс. Функция LargestPrimeGap не является, конечно, обратной в строгом смысле ни к функции CompositeRuns, ни к функции CompositeRunsStart, ни к написанной нами программе. Однако она делает нечто, что помогает "обратить" полученную нами таблицу. Давайте определим, например, длину наибольшего интервала из составных чисел, не превосходящих 11. Сначала вычислим наибольшую разность между двумя последовательными простыми числами, не превосходящими 11.
LargestPrimeGap[11] 4
Длина же интервала, естественно, на единицу меньше. И действительно, мы имели пару (3, 8}, что указывало, что первым числом в интервале длины 3 является 8. (Ну а 8+3 = 11.) Давайте теперь применим функцию LargestPrimeGap к нахождению наибольших разностей между двумя последовательными простыми числами, не превосходящими степеней некоторых чисел. В качестве оснований возьмем 2, е, 3, 5, 7, 10. Сначала попробуем провести вычисления, скажем, до 28 степени. Do[Print[{n,LargestPrimeGap[2An]}],{n,2,28}]
При выполнении этой программы получаются следующие результаты.
{3,2}
{4,4}
{5,6}
(6,6}
{7,14}
{8,14}
{9,14}
{10,20}
{11,34}
{12,34}
{13,34}
{14,44}
{15,72}
{16,72}
{17,72}
{18,86}
{19,114}
{20,114}
{21,148}
{22,148}
{23,154}
{24,154}
{25,210}
{26,220}
{27,222}
{28,248}
Отсюда видно, что основание 2 еще слишком мало, чтобы длина интервала изменялась существенно. Однако при вычислении последних значений на слабом компьютере ощущается заметное падение быстродействия. С чем это связано? Давайте перейдем к более естественному основанию — основанию натуральных логарифмов — и проверим, закономерно ли это.
Вот нужная нам программа.
Do[Print[{n, LargestPrimeGap[IntegerPart[ЕЛп]]}],{n,2,19}]
Вот что получилось.
{2,2}
{3,4}
{4,6}
{5,14}
{6,14}
{7,20}
{8,34}
{9,34}
{10,52}
{11,72}
{12,86}
{13,112}
{14,114}
{15,148}
{16,154}
{17,210}
{18,220}
{19,222}
Действительно, это основание кажется наиболее естественным, хотя все же нельзя не отметить хаотичность увеличения разностей и на этот раз. Но что подтвердилось — так это существенное падение быстродействия. Чтобы выяснить, с чем это связано, давайте запустим Диспетчер задач Windows. Изменим несколько нашу программу.
base=3;Do[Print[{n, LargestPrimeGap[baseAn]}],{n,2,17}]
Вот полученные результаты.
{2,2}
{3,4}
{4,6}
{5,14}
{6,18}
{7,34}
{8,34}
{9,52}
{10,72}
{11,86}
{12,114}
{13,132}
{14,154}
{15,154}
{16,210}
{17,222}
Когда быстродействие упало, я бы сказал, даже не до нуля, а до безобразия, я сделал копию экрана Диспетчера задач Windows (рис. 5.1). Из нее хорошо видна причина снижения быстродействия — слишком большой файл подкачки и высокая интенсивность страничного обмена. Из-за этого фактически система пробуксовывает, процент загрузки центрального процессора (ЦП) не повышается выше 30.
Теперь выполним наши вычисления для основания 5. На этот раз система Mathematica сама подскажет причину падения быстродействия.
base=5;Do[Print[{n,LargestPrimeGap[bаsе^n]}],
{n,2,17}] {2,4}-{3,8} {4,18} {5,34}
{6,36} {7,72} {8.,112} {9,132} {10,154}
{11,220} {12,248}
No more memory available.
Mathematica kernel has shutdown.
Try quitting other applications and then retry.
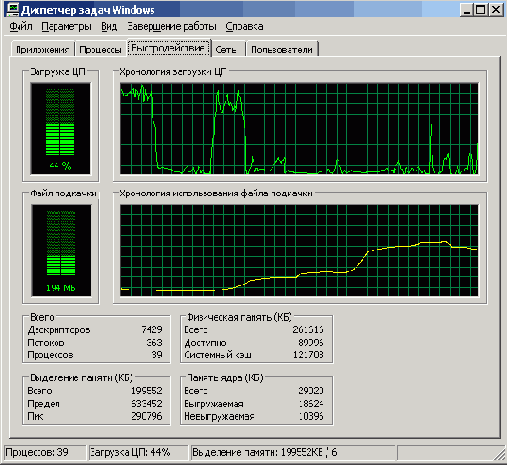
Рис. 5.1. Вот как растет файл подкачки
Хотя мы и получили довольно интересные результаты, завершение вычислений было несколько неожиданным. Давайте попробуем с основанием 7.
base=7;Do[Print[{n,LargestPrimeGap[bаsе^n]}],
{n,2,15}] {2,6} {3,14} {4,34} {5,44}
{6,72} {7,114} {8,154} {9,210}
На сей раз предупреждение не появилось, но вычисления пришлось прервать. На экране Диспетчера задач Windows хорошо видно плато, где загрузка ЦП высока, и почти отвесное ее падение (рис. 5.2).
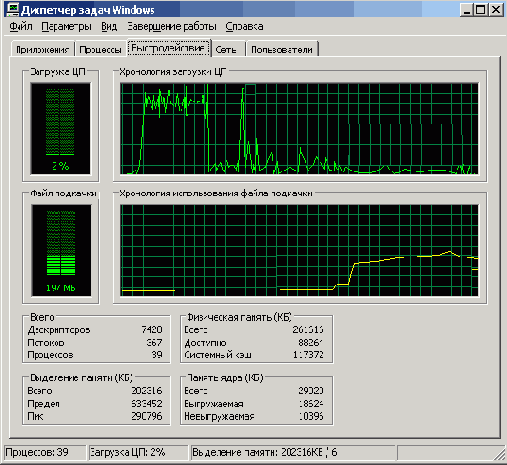
Рис. 5.2. Отчетливо видно плато Высокой производительности, рассеченное, правда, Каньоном вспомогательных действий. Плато Высокой производительности имеет почти отвесные обрывы
Наконец, проведем вычисления для основания, равного 10.
base=10;Do[Print[{n, LargestPrimeGap[base^n]}],{n,2,12}]
{2,8}{3,20}
{4,36} {5,72}
{6,114}
{7,154}
{8,220}
No more memory available.
Mathematica kernel has shut down.
Try quitting other applications and then retry.
На этот раз основание довольно велико, и картина на экране Диспетчера задач Windows очень отчетливая (рис. 5.3).
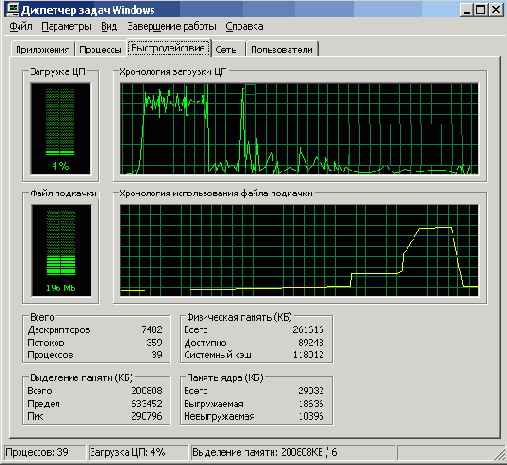
Рис. 5.3. Отчетливо видно не только плато Высокой производительности, но и почти отвесный обрыв Холма увеличения файла подкачки, связанный с завершением работы системы Mathematica
У всякой истории есть мораль, и эта не исключение. Некоторые функции, даже если они описаны в справочной системе (именно оттуда я взял функцию LargestPrimeGap), иногда требуют неоправданно большого объема памяти. Недостаточный объем памяти может помешать получить нужные результаты. Даже ночной прогон в таких случаях не помогает.
Давайте посмотрим, можно ли исправить ситуацию. Сначала загрузим пакет теории чисел.
<<NumberTheory`NumberTheoryFunctions`
Теперь определим функцию LargestPrimeGap01.
LargestPrimeGap01[n_]:=
Block[(pl=2,p2=3,i=2,pk=PreviousPrime[n+1],d=Max[n-pk,1]},
Whilefp2<pk,{pl=p2;
p2=NextPrime[p2];delta=p2-pl;
If[delta>d, d=delta]}];d]
В определении этой функции мы воспользовались функцией previousPrime[n], которая генерирует наибольшее простое число, меньшее n, и функцией NextPrime[n], которая генерирует наименьшее простое число, большее n. Вот небольшой тест.
LargestPrimeGap01[11] 4
Этот тест функция выдержала. Теперь можем перейти к главному экзамену.
base=10;Do[Print[{n, LargestPrimeGap01[bаsе^n]}},
{n,2, 9}] {2,8} {3,20} {4,36} {5,72}
{6,114} {7,154} {8,220} {9,282}
На этот раз, как видите из рис. 5.4, загрузка ЦП не падает, и потому при нехватке дневного времени ночной прогон программы вполне может спасти ситуацию.

Рис. 5.4. Отчетливо видно, что файл подкачки не растет, а загрузка ЦП не падает ниже 50% несмотря ни на какие переключения задач
В теории чисел длина наибольшего из интервалов между 1 и х, не содержащих простых чисел, обычно обозначается через g(x). Например, g(200) = 14, поскольку самым длинным таким интервалом при х=200 является интервал от 113 до127. Как мы видели, величина g(x) растет очень неравномерно, однако некоторые эвристические соображения, подкрепленные статистическими данными, приводят к асимптотической формуле g(x)~(lnx)2. Давайте все-таки проверим на графике, насколько хорошо
согласуется с ожидаемым поведением эта чрезвычайно скачущая функция. Сначала нарисуем график на интервале (1, 1000).
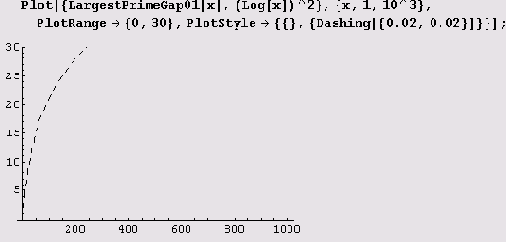
Похоже мало, но неплохо бы уточнить.

Вот еще одно уточнение.

И, наконец, нарисуем график на интервале (1,1 000 000).
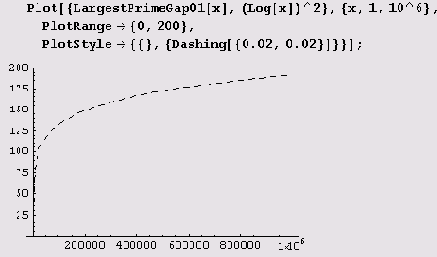
Конечно, похоже. Но не более, чем статистика на правду...
Пример 5.9. График разностей между последовательными простыми числами.
Давайте теперь построим график разностей между последовательными простыми числами. Сначала мы используем функции Table и Prime для построения таблицы t1 (точнее, списка) первых n простых чисел.
t1= Tablet Prime[k],{k,1,n=10Л5}];
Теперь составим таблицу t2 (тоже список) разностей между последовательными простыми числами.
t2=Table[t1[[i+1]]-t1[[i]], {i,1,Length[t1]-1}];
Наконец, мы можем использовать функцию ListPlot для построения графика.

А вот график для n = 10000.
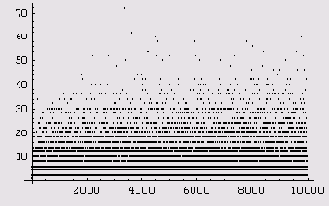
Близнецы
Изучая распределение простых чисел, мы узнали, что интервалы, состоящие из составных чисел, могут быть сколь угодно длинными. Однако встречаются и очень короткие интервалы, ограниченные простыми числами. Простые числа 2 и 3 следуют друг за другом, не пропуская между собой ни одного составного числа. Но это, конечно, исключение, больше нигде не встречающееся в натуральном ряду. Но зато немало встречается таких пар простых чисел, между которыми стоит только одно составное число (четное, естественно). Простые числа, разность которых равна 2, называются близнецами. Честно говоря, это наименьшая возможная разность между нечетными простыми числами. (Потому что все простые числа, за исключением 2, нечетны!) Вот как определяется функция, которая отыскивает все пары близнецов среди первых т простых чисел.
TwinPrimes[m_]:=
Module[{s=Prime[Range[m]]},
{#,#+2}&/@Extract[s,Position[Dropfs,1]- Drop[s,-l],2]]]
Вот, например, список пар близнецов среди первой тысячи простых чисел.

А вот так можно найти список пар близнецов, не превосходящих 1000.

В принципе данная функция работает довольно быстро, хотя едва ли она может найти пару близнецов {156-5202-1 , 156-5202 +1}.
Простые числа, близкие к числам определенного вида
В ряде областей науки и техники, например в теории кодирования, важно знать простые числа, близкие к числам определенного вида (чаще всего к степеням таких оснований, как 2, 3 и 10). Вне сомнения, их можно было бы найти в обычных таблицах простых чисел. Однако таблицы нужного размера не могли бы поместиться даже в многотомных изданиях. Поэтому существуют специальные таблицы, в которых приводятся только простые числа, близкие, например, к 2n, 3n и 10n.
Но составить такие таблицы для достаточно больших n довольно трудно, и, несмотря на компактность, такие таблицы зачастую весьма неполны. С помощью системы Mathematica несложно составить такие таблицы самостоятельно. Допустим, таблица должна содержать десять наибольших простых чисел, предшествующих N, и десять простых чисел, следующих за N. Можно ограничиться случаем достаточно больших N, например N>1000, поскольку при меньших N вопрос решается с помощью таблиц простых чисел, помещаемых обычно в учебниках для пятиклассников.
Давайте попытаемся составить нужную нам программу, например, для степеней 10. Чтобы результаты выглядели наглядно, нужно предусмотреть их преобразование в таблицу с помощью текстового процессора, например, Word. Поэтому необходимо предусмотреть такой формат результатов, который было бы легко отформатировать (преобразовать в таблицу). Для этого можно предусмотреть двоеточие : в качества разделителя колонок и два двоеточия : : в качестве разделителя строк таблицы. Вот как может выглядеть программа.
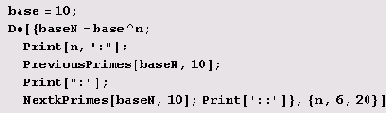
В этой программе использованы функции PreviouskPrimes и NextkPrimes. Функция PreviouskPrimes [N, k] должна генерировать k наибольших простых чисел, меньших Ж Иными словами, она должна генерировать k простых чисел, предшествующих N. Функция NextkPrimes [N, k] должна генерировать k наименьших простых чисел, больших N. Иными словами, она должна генерировать k простых чисел, следующих за N. Вот и все. Нам осталось только написать код этих двух функций. Давайте начнем с функции PreviouskPrimes [N, k].
PreviouskPrimes[n_Integer?(#>100&)
, k_Integer?Positive]:=
Block[{p=PreviousPrime[n] , i=l},
While[i<=k,
{Print[p,","],
p=PreviousPrime[p],++i}]]
Эта функция генерирует простые числа в порядке убывания, т.е. в порядке удаления от заданного числа, что удобно при выборе простого числа, наиболее близкого к заданному.
Не сложнее написать и функцию NextkPrimes [N, k]. Для этого нужно только заменить функцию PreviousPrime на NextPrime.
NextkPrimes[n_Integer?(#>100&) ,
k_Integer?Positive]: = Block[{p=NextPrime[n],i=l},
While[i<=k,{Print[p,","],
p=NextPrime[p] , + + i} ]]
Теперь можем приступить к выполнению составленной программы. Так как функции PreviousPrime и NextPrime содержатся в пакете теории чисел, в первую очередь нужно загрузить этот пакет.
<<NumberTheory`NumberTheoryFunctions`
Затем нужно загрузить (и проверить) определения наших функций PreviouskPrimes и NextkPrimes. Сначала загрузим (и протестируем) PreviouskPrimes.
PreviouskPrimes[n_Integer?(#>100&),
k_Integer?Positive]:= Block[{p=PreviousPrime[n],i=l},
While[i<=k,(Print[p,","],
p=PreviousPrime[p]/++i}]]
PreviouskPrimes[1000,3]
997 ,
991 ,
983 ,
Видим, что функция PreviouskPrimes работает правильно. Значит, теперь можем сделать то же самое и для функции NextkPrimes.
NextkPrimes[n_Integer?(#>100&),
k_Integer?Positive]:= Block[{p=NextPrime[n],i=l},
While[i<=k, {Print[p,","],p=NextPrime[p],++i} ]]
NextkPrimes[1000,3]
1009 ,
1013 ,
1019 ,
Теперь можем ввести программу и выполнить ее. Вот что у нас получится (конец обрезан).
6 : <
999983 999979 999961 999959 999953
999931 999917 999907 999883 999863
1000003 1000033 1000037 1000039
1000081 1000099 1000117 1000121 1000133 1000151
7 :
9999991 ,
9999973 ,
9999971 ,
9999943 ,
Конечно, для практического применения результаты удобнее отформатировать в виде таблицы. Для этого в текстовом редакторе нужно сделать всего несколько замен. Сначала нужно убрать пробелы, разрывы строк, символы абзацев (кроме последнего) и запятые перед двоеточием. Затем два двоеточия нужно заменить символом абзаца. Этим самым мы разобьем таблицу на строки. После этого достаточно выделить все, что получилось, и преобразовать текст в таблицу, указав в качестве разделителя столбцов двоеточие :. Конечно, это еще не все. Нужно ведь еще расставить пробелы после запятых, написать название таблицы и заголовки столбцов.
Число простых чисел, не превосходящих х (функция PrimePi[x])
Согласитесь, изучив все тонкости искусства составления таблиц простых чисел, было бы нелогично пренебречь искусством составления таблиц на основе уже созданных. Почему бы, имея полную (значит, бесконечную!) таблицу простых чисел, не поинтересоваться, сколько чисел в этой таблице не превосходят данного числа х. Иными словами, определить число простых чисел, не превосходящих х. Это число в учебниках теории чисел обозначается л(х). Функция п(х) привлекала внимание уже античных математиков. Евклид, например, установил, что она неограниченно возрастает с ростом аргумента. Изучением этой функции занимались почти все великие математики Прошлого, ее исследовали Лежандр, Чебышев, Риман, Адамар, Валле-Пуссен, Чудаков, Виноградов, Коробов, Литлвуд, Сельберг, Эрдеш, Ингам, Прахар, Пан Чен-тонг, Чен-ин-рун, Титчмарш, Мейссель, Рогель, Чипола, Мертенс, Гаусс, Бертран, Вейль, Линник, Бомбьери...
В системе Mathematica эта функция называется PrimePi. Система Mathematica может вычислить ее значения практически в мгновение ока... Правда, не все.

В документации, правда, верхний предел указан примерно равным 260, а на самом деле...

Тем не менее не следует воспринимать ситуацию уж очень пессимистически. Давайте, например, построим графики функций 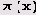
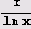 на промежутке (0, 100).
на промежутке (0, 100).

Как видите, если не считать неприятностей с нулем, где 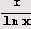
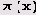 . Впрочем, вот график с интегральным логарифмом.
. Впрочем, вот график с интегральным логарифмом.

Теперь даже в нуле неприятностей нет. Но вот вопрос: будет ли заметна ступенчатость на больших интервалах? На самом деле ступенчатость незаметна уже на интервале (0, 10000).
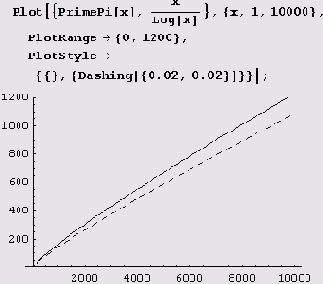
Но какая же функция приближает 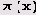
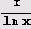 или Li(x)? Конечно, Li(x).
или Li(x)? Конечно, Li(x).
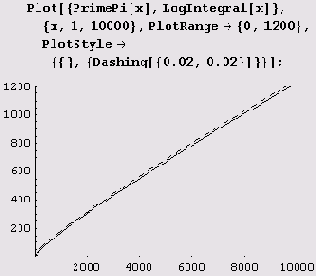
Если же построить график на интервале (0, 10000), то графики 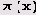

Раз уж речь зашла о приближении k(х), давайте построим графики разности функции 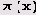
 (приближение Чебышева и Лежандра), в качестве второй — 1л(х) (приближение Гаусса), а в качестве третьей — R(x) (приближение Римана). Сначала определим функцию R(x).
(приближение Чебышева и Лежандра), в качестве второй — 1л(х) (приближение Гаусса), а в качестве третьей — R(x) (приближение Римана). Сначала определим функцию R(x).
Riemann[x_]:=
Last[Block[{R=LogIntegral[x],y=LogIntegral[Sqrt[x]]/2,n=2},
{While[y>0.000000001,{R=R-y; n=n+l;y=LogIntegral[х^(1/n)]/n}
],R} ]]
Теперь можем построить нужные нам графики.
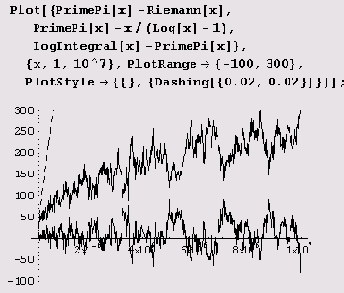
Как видим, из трех наилучшим является приближение Римана. И еще одно замечание. Как мы видели, график функции π(х) выглядит вполне гладко, хотя на самом деле он является ступенчатым. Более того, существуют сколь угодно длинные интервалы, на которых он горизонтален. Однако длина таких интервалов незначительна по сравнению с их расстоянием до начала координат. Это интервалы, на которых функция π(x) не изменяется. Иными словами, это интервалы, на которых нет простых чисел. Кстати, а как сосчитать количество простых чисел на интервале (а, b] ?
Количество простых чисел на открытом слева отрезке (а, b]
С помощью функции PrimePi несложно подсчитать и количество простых чисел на открытом слева отрезке (а, b]. Помните только, что если вы пользуетесь выражением k(b)-n(а), т.е. выражением PrimePi [b] -PrimePi [a], то в случае простоты простое число b будет посчитано, а простое число а — нет. Иными словами, подсчет осуществляется на открытом слева отрезке (а, b]. А что, если нужно посчитать простые числа на замкнутом с обоих концов отрезке [а, b}1 Ничего сложного: в качестве аргумента можно взять не а, а несколько меньшее число, ведь аргументом функции PrimePi может быть любое вещественное положительное число. Давайте посчитаем, например, количество простых чисел в 1-й, 2-й, ... , 20-й сотне миллионов натуральных чисел. Вот как это можно сделать.
delta=100000000;
PrimePiAB[delta_Integer?Positive,xk_Integer?Positive]:=
Block[{k=0, x=delta, kt=0 },
While[x<=xk,
{kt=PrimePi[x];
Print[x,":",kt,":",kt-k];
k=kt; x=x+delta}]]
PrimePiAB[delta,10 delta]
Полученные результаты удобно представить в виде таблицы .
В приведенной выше программе мы воспользовались тем, что интервалы примыкают друг к другу. Однако так бывает не всегда. Иногда нужно подсчитать количество простых чисел в интервалах заданной длины, причем начала интервалов расположены на числовой оси так, что конец очередного интервала не совпадает с началом следующего. Подсчитаем, например, количество простых чисел в интервалах длиной 150000, причем пусть начинаются эти интервалы в точках х= 106, 107, ... , 1014. Для этого случая пригодится следующая функция.
DeltaPi[x_,delta_]:=
Block[{xk=x+delta,k=PrimePi[xk]},
Print[x,"-",xk,":",k-PrimePi[x]]]
С помощью этой функции нетрудно написать и нужную нам программу.
delta=150000;
Do[DeltaPi[10^n,delta],{n,6,14)]
Результаты отформатированы в виде таблицы.
Хотя каждый математик знает, ох,
Хотя каждый математик знает, ох, как это непросто, нужно признать, что система Mathematica дружит с простыми числами. В ней есть функции, проверяющие, является ли число простым; функция, генерирующая n-е простое число; функция, генерирующая следующее простое число; функция, генерирующая предыдущее простое число; а также знаменитая функция n(х), подсчитывающая количество простых чисел, не превосходящих заданного числа х. Конечно, реализовать все эти функции весьма непросто, и применяя их, нужно учитывать ограничения на их аргументы. Но как бы то ни было, в системе Mathematica они реализованы на современном уровне, с учетом совсем недавно доказанных теорем и новых методов.