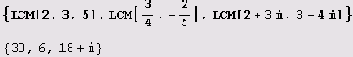Наибольший общий делитель — функция GCD

Функция GCD находит наибольший общий делитель в области целых, рациональных и гауссовых чисел.

Наибольший общий делитель в кольце целых чисел

Чтобы найти наибольший общий делитель чисел n₁, n₂, ..., можно использовать функцию GCD [ n₁, n₂, ...]. Вот примеры ее применения для нахождения наибольшего общего делителя двух чисел.

GCD[36,45]

9 GCD[2200 + 3, 3300 + 80]

349

а=177^5+30621*173^3-173^5 177309584821

b=173^5+30621*177^3-177^5+

151037867129 С=173^4+30621^2+177^4 2814896923

 GCD[a,b] 30637 GCD[а,с] 30637 GCD[b,c]30637

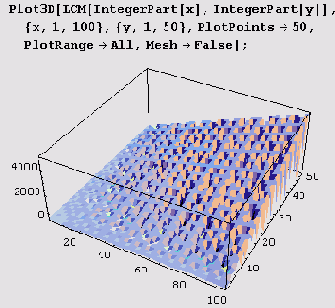
Пример 6.1. Графики функции GCD.

Давайте теперь построим несколько графиков функции GCD. Поскольку это функция двух аргументов, построим изображения поверхности z = GCDflntegerPart [x], IntegerPart [у] ]. Для этого используем функцию Plot3D.

А вот вид вблизи.

Вот пример нахождения наибольшего общего делителя нескольких чисел.

GCD[Fibonacci[945],Fibonacci[901,Fibonacci[450]]

1134903170

Раз уж мы заговорили о числах Фибоначчи, значит, мы не можем обойти случаи, которые традиционно считаются "наихудшими" для алгоритмов нахождения наибольшего общего делителя.

"Наихудшие" случаи для алгоритмов нахождения наибольшего общего делителя

"Наихудшим" случаем для классического алгоритма Евклида нахождения наибольшего общего делителя считается случай соседних чисел Фибоначчи. Чтобы оценить быстродействие, попытаемся, например, определить, при каком n будет заметна задержка при вычислении GCD[Fibonacci [n+2] (Fibonacci[n+1]]. Возьмем, например, следующую программу.

Do[Print[n,":",GCD[Fibonacci[n+2],Fibonacci[n+1]]],(n, 10000}]

Увы! Алгоритм, реализованный в системе Mathematica, столь эффективен, что даже на весьма посредственном ПК эта программа выполняется без каких бы то ни было задержек. Если же программу модифицировать так:  Do[Print[n,":",GCD[Fibonacci[2An+2], Fibonacci[2An+1]]],{n,10000}] ,то задержка будет весьма ощутимой уже при n = 25. Но не забывайте, что 225 + 2 =33554434, а число Fibonacci[2^25+2] имеет 7012462 цифры! Так что алгоритм, реализованный в системе Mathematica, справляется с классическим "наихудшим" случаем не просто вполне удовлетворительно, а блестяще! Правда, известны алгоритмы, для которых наихудший случай представляют числа u = аn +а_n-1, и v= а_n-1, где 

a[n_]:=FullSimplify[((1+Sqrt[2])^n-(1-Sqrt[2])^n)/(2Sqrt[2])]

u:=a[n]+a[n-l]

v:=a[n-l]

Попытаемся выполнить программу.

Do[Print[n,":",GCD{u,v]],{n,100}]

Окажется, что уже при n = 98 выражения "не хотят" упрощаться! Поэтому определение а[n_] лучше изменить.

а[n_]:=(Expand[(1+Sqrt[2])^n]-Expand[(1-Sqrt[2])^n])/(2 Sqrt[2])

Однако при таком подходе понятно, что значительное время тратится также на раскрытие скобок. Однако даже при n = 70 000 вычисления не занимают слишком много времени. При этом значении и числа u и v являются 26 794-значными, и основное время уходит на их вычисление, а не на вычисление их наибольшего общего делителя, который вычисляется в мгновенье ока! Отсюда можем сделать вывод, что функция GCD реализована весьма эффективно, и если при ее использовании возникают неприятности, то, скорее всего, они связаны с вычислением не самой функции, а ее аргументов!

Пример 6.2. Взаимная простота чисел Ферма. Числа Ферма возрастают довольно быстро и являются взаимно простыми. Поэтому их наибольший общий делитель должен быть равен 1. Выясним, до какого номера n система Mathematica сможет в приемлемое время проверить взаимную простоту этих чисел.

Вот нужная нам функция.

fermat[n_]:=2^(2^n)+1

Теперь можно написать и программу.

Do[Print(n,":",GCD[fermat[n+1], fermat[n]]],{n,100}]

Задержка начинает ощущаться при n = 28. Однако вычисления заканчиваются (и притом довольно быстро, если учитывать количество цифр в числах) и при n= 29. Напомню, что уже 22-е число Ферма имеет более миллиона (1 262 612) знаков, а 23-е число Ферма является 2 525 223-значным! Шутки ради 24-е число Ферма, являющееся 5 050 446-значным, я перетащил в Word. Текстовый редактор с записью этого числа работает медленнее, чем система Mathematica! Вот уж воистину супервычислитель: решает задачу быстрее, чем иные успевают произнести ее формулировку! 25-е число Ферма является 10 100 891-значным, и Word его не выносит: замедляется работа меню, даже курсор движется так медленно, что работать становится практически невозможно.

Пример 6.З. Взаимная простота чисел 2ⁿ -1 и 2^m -1 при взаимно простых лит. Как известно, числа 2ⁿ-1 и 2^m -1 взаимно просты, если взаимно просты пит. Выясним, до какого номера n(предполагая, что т<п) система Mathematica сможет в приемлемое время проверить взаимную простоту этих чисел.

Вот нужная нам функция.

fn[n_]:=2^n-1

Теперь можно написать и программу.

Dot

Do[

If[GCD[n,m]==1,If[GCD[fn[n], fn[m]]!=l,

Print[n,":",m]]],{m,n-l}],{n,10000}]//Timing

Для первой тысячи чисел все проверки на моем весьма слабеньком ПК выполняются всего лишь за 8,125 секунды! Правда, для проверки этого утверждения в пределах первых десяти тысяч чисел понадобится уже 3398,78 секунды. Здесь, очевидно, сказывается не только увеличение и, но и увеличение временных затрат на нахождение наибольшего общего делителя больших чисел.

Пример 6.4. Наибольший общий делитель чисел, запись которых в десятичной системе состоит из т единиц и n единиц. Как известно, наибольший общий делитель чисел, запись которых в десятичной системе состоит из m единиц и n единиц, является числом того же вида, причем количество единиц в нем равно d= НОД(n, m). Выясним, сколько времени системе Mathematica понадобится для проверки этого утверждения для n, т, не превосходящих 1000.

Вот нужные нам определения.

a111[n_]:=(10^n-1) /9 d:= GCD[n, m]

Теперь можно написать и программу.

Dot

Dot

If[GCD[alll[n], a111[m]]!=alll[d],

 Print[n,":",m]],{m,n-l}],{n,1000}]//Timing

Проверка в пределах первой сотни занимает всего лишь 0,234 секунды, хотя при этом наибольшее число указанного в условии вида имеет 100 цифр! Проверка же в пределах первой тысячи у меня потребовала в 200 раз больше — 46,594 секунды. Чтобы выполнить проверку в пределах первых пяти тысяч, потребуется 6879,67 секунды.

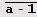
Пример 6.5. Наибольший общий делитель чисел аⁿ -1 и а^m -1. Как известно, наибольший общий делитель чисел аⁿ -1 и а^m -1, запись которых в системе счисления с основанием а состоит из n цифр    является числом того же вида, причем количество цифр й-1 в нем равно d= НОД(n, m). Выясним, сколько времени системе Mathematica понадобится для проверки этого утверждения для n, т, не превосходящих 1000.

Вот нужные нам определения.

ааа[а_,n_]:=аЛп-1; d:= GCD[n, m]

Теперь можно написать и программу.

Do[ Dot Dot

If[GCD[aaa[n,a],aaa[m,a]]!=aaa[d],

Print[n,":",m]] ,

{m,n-l}], {n,100}], {a,100}]//Timing

Для выполнения этой программы потребуется 19,797 секунды. Весьма впечатляющий результат!

Пример 6.6. Наибольший общий делитель чисел Фибоначчи. Проверим, что наибольший общий делитель n-го и m-го чисел Фибоначчи равен числу Фибоначчи с номером d = НОД(n, m). Иными словами, проверим, что НОД (Fibonacci [n], Fibonacci [m]) = Fibonacci [НОД (n,m) ]. Выясним, сколько времени системе Mathematica понадобится для проверки этого утверждения для n, т, не превосходящих 1000.

Вот нужное нам определение.

d:= GCD[n, m]

Теперь можно написать и программу.

Do[

Do[

If[GCD[Fibonacci[n], Fibonacci[m]]!= Fibonacci[d],

 Print[n,":",m]]

, {m,n-l}],

{n,1000}]//Timing

Для выполнения этой программы потребуется всего лишь 15,75 секунды.

Наибольший общий делитель в поле рациональных чисел

Наибольший общий делитель рациональных чисел r₁, r₂, ... определяется как наибольшее рациональное число г, такое, что все числа r₁/r, r₂ /r, ... являются целыми. Вот пример.

Наибольший общий делитель в кольце гауссовых чисел

Функция GCD может найти наибольший общий делитель не только в кольце целых чисел, но и в кольце целых гауссовых чисел.

GCD[21+28I,-33-44I] 3 + 4 I

Линейное представление наибольшего общего делителя — функция ExtendedGCD

В ряде задач необходимо найти не только наибольший общий делитель нескольких чисел, но и его представление в виде линейной комбинации этих чисел. Именно эту задачу решает функция ExtendedGCD. Функция ExtendedGCD [ n₁, n₂, ...] возвращает список {g, { r₁ , r₂, ...}}, такой, что g= GCD [n_1, n₂, ...] и g = r₁n₁+r₂n₂ + .... Вот примеры.

{g,{r,s}}=ExtendedGCD[n=45,m=36]

(9,{!,-!}}{g,{r,s}}=ExtendedGCD[210°+3,З50 + 8]

{1,{62013782892351778750374,-109502757290992473821761130785} }

Пример 6.7. Единица как линейная комбинация чисел Ферма. Так как числа Ферма являются взаимно простыми, их наибольший общий делитель равен единице. Выясним, как единица представляется в виде линейной комбинации соседних чисел Ферма.

Вот нужная нам функция.

FermatNumber[n_]:=2^(2^n)-N

Теперь можно написать и программу.

Do[Print[n,":",ExtendedGCD[FermatNumber[n+1],

FermatNumber [n]]],{n,10}]

Результаты запишем в виде таблицы.

Заметьте, что в таблице при n>1 числа r_n заканчиваются цифрой 8, а числа s_n— цифрой 1.

Пример 6.8. Единица как линейная комбинация чисел 2_n-1 и 2_m-— 1 при взаимно простых пит. Так как числа 2ⁿ -1 и 2^m -1 взаимно просты, если взаимно просты n и m, то единицу можно представить в виде линейной комбинации чисел 2ⁿ -1 и 2^m-1 при взаимно простых пит. Выясним, до какого номера n(предполагая, что т<п) система Mathematica сможет в приемлемое время проверить взаимную простоту этих чисел.

Вот нужная нам функция.

fn[n_]:=2^n-1

Теперь можно написать и программу.

Do[

Dot

If[GCD[n, m]==l, Print[n,":",m, ":",

 ExtendedGCD[fn[n],fn[m]]]],{m,n-l}],(n,10}]

Результаты запишем в виде таблицы .

Заметьте, что довольно часто в данной таблице встречается пара r = 1,5= -2. Это не случайно, поскольку при n = n+1 выполняется равенство -(2ⁿ -1)+2-(2(ⁿ -1) = -1.

Пример 6.9. Линейное представление наибольшего общего делителя чисел, десятичная запись которых состоит из m единиц и n единиц. Наибольший общий делитель чисел, десятичная запись которых состоит из т единиц и п единиц, является числом того же вида, причем количество единиц в нем равно d = НОД(n, m). Выясним, как он представляется в виде линейной комбинации.

Вот нужные нам определения.

a111[n]:=(10^n-1)/9 d: = GCD[n, m]

Теперь можно написать и программу:

Dot

Dot

Print[n,":",m,":",

 ExtendedGCD[alll[n],alll[m]]],{m,n-l}],{n,10}]

Заметьте, что десятичная запись чисел r и s в данной таблице содержит только цифры 0 и 1. Я не удивлюсь, если вы предположите, что это связано с наличием некоторых полиномиальных тождеств и потому значения г и s получаются в результате подстановки 10 (основания системы счисления) в них. Например, строку таблицы

9

6

111

1

-1000

можно истолковать так:

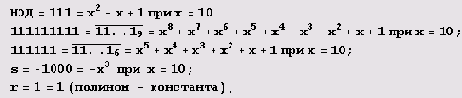
s = -1000 = -x³ при х = 10;

r = 1 = 1(полином-константа); поэтому

х² +х + 1 = 1*(x⁸ +х⁷ + х⁶ + х⁵ + х⁴ + х³+х² +х + 1) + (-x³)-(x⁵ +х⁴ + x³ + х² +х+ 1) при х = 10. Однако само это равенство выполняется при любом g:, а не только при дс = 10. Значит, в качестве г и s можно взять числа, имеющие точно такое же представление в любой системе счисления, а не только в десятичной! Конечно, наличие строки в таблице еще не означает автоматически тождественную справедливость соответствующего равенства, это лишь означает, что соответствующее равенство справедливо при х = 10. Поэтому вполне возможно, по крайней мере теоретически, что нам просто повезло. Если говорить честно, так оно и есть. Дело ведь в том, что по равенству d = ra+sb (d = НОД(a, b)) числа r и s определяются неоднозначно: если d = ra+sb, то d = (r+b)a+(s—a)b и d = (r—b)a+(s+a)b. Иными словами, если d = ra+sb, то d= r'a+s'b (при r'= r+b и s' = s-а) и d— r"a+s"b (при r" = r-b и s"= s+d). Так что наличие строки еще не означает наличие тождества. Но, с другой стороны, числа г и s определяются однозначно, если на них наложить ограничения |r <b и |s| <a. Более того, все пары значений г и s можно получить, несколько раз выполняя переход от какой-либо пары фиксированных значений г0 и s0 к новой паре значений по правилам г' = г+b и s'= s-a или r' = r-b и s'= s+a.

Конечно, наличие полиномиальных тождеств сомнений не вызывает, ведь наибольший общий делитель полиномов (х) = x^n-1 + х^n-2 + x^n-3 +... + х +1 и b(х) = х^m-1+х^m-2+х^m-3 + ... + х+1 равен d(x) = x^d-1 + x^d-2 + х^d-3 +... + х +1, где d = НОД(n ,m).

Так как он представим в виде линейной комбинации а(х) — х^n-1 + х^n-2 + х^n-3 +... + х +1 и b(х) = х^m-1 + х^m-2 + х^m-3 +... + х+1, то имеет место равенство d(x) = r(x)a(x)+s(x)b(x). Более того, полиномы г(х) и s(x) можно выбрать так, чтобы deg r(x)<m и deg s(x)<n. Проблема, собственно, состоит вот в чем. По числам а и b мы без труда восстановили полиномы а(х) = x^n-1+ х^n-2 + x^n-3 +... + xⁿ +1 и b(х) =х^n-1+х^n-2+х^n-3+... + х + 1, но можем ли мы так же просто восстановить и полиномы г(х) и 5(х)?

Предположим теперь, что для равенства d = ra+sb (d = НОД(я, b)) с \r\ <b и \s\ <a мы написали равенство полиномов того же типа, что и приведенное выше. Запишем это равенство в виде d(x) = r(x)a(x)+s(x)b(x). Разумеется, здесь а(х) = х^n-1+х^n-2+х^n-3+... + х + 1 и b(х) = x^n-1 +х^n-2+ х^n-3+ ... + Х + ] .Поскольку a<b и |s| <a, то deg r(x)<m и deg s(x)<n, а потому правая часть найденного тождества есть полином степени не выше m+n. Тогда, как известно, чтобы проверить написанное равенство, достаточно проверить его при т+п+1 значении х. (Конечно, такую проверку совсем несложно запрограммировать в системе Mathematica.) Но можно поступить и иначе. Достаточно убедиться, что представление г и s будет одинаковым для т+п+1 значений основания системы счисления. (Ведь фактически это будет означать, что равенство полиномов степени не выше m+n выполняется при n+m+1 значении х.) Именно таким способом мы и поступим в следующем примере. (Вопрос о том, есть ли среди найденных представлений такие, которые основаны не на полиномиальных тождествах, намеренно оставляю открытым. Впрочем, вот подсказка: ответ знают некоторые студенты мехмата уже на первом семестре. Я, конечно, совсем не имел в виду, что это написано в учебниках или обязательно излагается на лекциях, но догадаться можно.)

Пример 6.10. Линейное представление наибольшего общего делителя чисел аⁿ-1 и

а^m -1. Наибольший общий делитель чисел а" -1 и а" -1, запись которых в системе счисления с основанием а состоит из и цифр  , является числом того же вида, причем количество цифр я-1 в нем равно d= НОД(n, m). Выясним, как наибольший общий делитель чисел аⁿ -1 и а^m -1 представляется в виде их линейной комбинации.

Вот нужные нам определения.

ааа[а_,n_]:=аАп-1; d:= GCD[n, m]

Теперь можно написать и программу. Нужно только не забыть о том, что представление r и s лучше всего получить в системе счисления с основанием я. Для этого вполне подойдет функция IntegerDigits. Она, правда, теряет знак числа, так что его придется печатать отдельно.

Do[ Dot Dot

{{g,(r,s}}= ExtendedGCD[aaa[a,n],aaa[a,m]],

Print["###", n, ":",m,":",d,":",a,":"],

If[g<0,Print["-"]],

Print[IntegerDigits[g,a], ":"],

If[r<0,Print!"-"]],

Print[IntegerDigits[r,a], ":"],

If [s<0,Print["-"]],

Print[IntegerDigits[s,a]]} ,

{a,2,n+m+2}],{m,n-l}],{n,10}]

Заметьте, что в программе вставлена печать fit для удобства форматирования результатов.

Скажу сразу, что более скучной таблицы я, наверное, никогда не видел! И все из-за удивительного постоянства г и s! Представление r и s выглядит одинаково в системах счисления с разными основаниями, и потому их представления просто повторяются во многих строках! Это значит, что представление наибольшего общего делителя действительно основано на полиномиальных тождествах вида d(x) = r(x)a(x)+s(x)b(x), причем полиномы r(х) и s(x) легко восстанавливаются по числам r и s! Конечно, я избавлю вас от демонстрации всего этого и просто приведу некоторые наиболее характерные строки таблицы. Разумеется, большинство строк aⁿ опустил, и таблица содержит пропуски. Они обозначены строками с многоточиями. Чтобы развеять сомнения, достаточно взглянуть вот на это.

Линейное представление наибольшего общего делителя чисел аⁿ - 1 и а^m -1:

НОД= r-(aⁿ-l) + s-(a^m-l)

n	m	d= НОД (n, m)	Основание системы счисления а	Цифры НОД в системе счисления с основанием а	Цифры r в системе счисления с основанием а	Цифры s в системе счисления с основанием а
2	1	1	2	(1)	{0}	{1}
2	1	1	3	{2}	{0}	(1)
2	1	1	4	{3}	{0}	{1}
2	1	1	5	Н)	{0}	(1)
3	1	1	2	{1}	{0}	{1}
3	1	1	3	{2}	{0}	{1}
3	1	1	4	{3}	{0}	{1}
3	1	1	5	{4}	{0}	(1)
3	1	1	6	(5)	{0}	{1}
3	2	1	2	(1)	{1}	-{1,0}
3	г	1	3	(2}	{1}	-{1,0}
3	2	1	4	(3)	{1}	-{1,0}
3	2	1	5	(4}	{1}	-{1,0}
3.	2	1	6	(5)	{1}	-{1,0}
3	2	1	7	(6)	{1}	-{1,0}
4	1	1	2	(1}	{0}	{1}
4	1	1	3	{2}	{0}	{1}
4	1	1	4	(3)	{0}	{1}
4	1	1	5	(4)	{0}	{1}
4	1	1	6	{5}	(0)	{1}
4	1	1	7	{6}	{0}	{1}
4	2	2	2	{1,1}	{0}	{1}
4	2	2	3	(2,2)	{0}	{1}
4	2	2	4	(3,3)	{0}	{1}
4	2	2	5 '	{4,4}	{0}	{1}
4	2	2	6	{5,5}	{0}	{1}
4	2	2	7	{6,6}	{0}	{1}
4	2	2	8	(7,7}	{0}	{1}
4	3	1	2	{1}	{1}	-{1,0.}
4	3	1	3	{2}	{1}	-{1,0}
4	3	1	4	{3}	{1}	-{1,0}
4	3	1	5	{4}	{1}	-{1,0}
4	3	1	6	{5}	{1}	-{1,0}
4	3	1	7	{6}	{1}	-{1,0}
4	3	1	8	{7}	{1}	-{1,0}
4	3	1	9	(81	(1)	-{1,0}
		..	...	...	...	...
5	2	1	2	{1}	{1}	-{1,0,1,0}
5	2	1	3	(2)	{1}	-{1,0,1,0}
5	2	1	4	(3}	{1}	-{1,0,1,0}
5	2	1	5	(4)	{1}	-{1,0,1,0}
5	2	1	6	{5}	{1}	-{1,0,1,0}
5	2	1	7	{6}	{1}	-{1,0,1,0}
5	2	1	8	{7}	{1}	-{1,0,1,0}
5	2	1	9	(8)	{1}	-{1,0,1,0}
5	3	1	2	(1)	-{1,0}	{1,0,0,1}
5	3	1	3	{2}	-{1,0}	{1,0,0,1}
5	3	1	4	(3}	-{1,0}	{1,0,0,1}
5	3	1	5	{4}	-{1,0}	{1,0,0,1}
5	3	1	6	{5}	-{1,0}	{1,0,0,1}
5	3	1	7	{6}	-{1,0}	{1,0,0,1}
5	3	1	8	{7}	-{1,0}	{1,0,0,1}
5	3	1	9	(8)	-{1,0}	{1,0,0,1}
5	3	1	10	{9}	-{1,0}	{1,0,0,1}
5	4	1	2	{1}	{1}	-{1,0}
5	4	1	3	{2}	{1}	-{1,0}
5	4	1	4	(3)	{1}	-{1,0}
5	4	1	5	{4}	{1}	-{1,0}
5	4	1	6	(5}	{1}	-{1,0}
5	4	1	7	{6)	{1}	-{1,0}
5	4	1	8	{1}	{1}	-{1,0}
5	4	1	9	{8}	{1}	-{1,0}
5	4	1	10	{9}	{1}	-{1,0}
5	4	1	11	{10}	{1}	-{1,0}
...		...	...	...	...	...
7	2	1	2	{1}	11}	-{1,0,1,0,1,0}
7	2	1	3	(2)	{1}	-{1,0,1,0,1,0}
7	2	1	4	{3}	{1}	-{1,0,1,0,1,0}
7	2	1	5	{4}	{1}	-{1,0,1,0,1,0}
7	2	1	6	{5}	{1}	-{1,0,1,0,1,0}
7	2	1	7	{6}	{1}	-{1,0,1,0,1,0}
7	2	1	8	(7)	(1)	-{1,0,1,0,1,0}
7	2	1	9	{8)	{1}	-{1,0,1,0, 1,0}
7	2	1	10	{9}	{1}	-{1,0,1,0,1,0}
7	2	1	11	{10}	{1}	-{1,0,1,0,1,0}
7	3	1	2	{1}	{1}	-{1,0,0,1,0}
7	3	1	3	{2}	(1)	-{1,0,0,1,0}
7	3	1	4	{3}	{1}	-{1,0,0,1,0}
7	3	1	5	{4}	{1}	-{1,0,0,1,0}
7	3	1 i	6	{5}	{1}	-{1,0,0,1,0}
7	3	1	7	{5}	{1}	-{1,0,0, 1,0}
7	3	1	8	{8}	{1}	-{1,0,0,1,0}
7	3	1	9	{8}	{1}	-{1,0,0,1,0}
7	3	1	10	{9}	(1)	-{1,0,0,1,0}
7	3	1	11	{10}	{1}	-{1,0,0,1,0}
7	3	1	12	{11}	{1}	-{1,0,0,1,0}
7	4	1	2	{1}	-{1,0}	{1,0,0,0,1}
7	4	1	3	{2}	-{1,0}	{1,0,0,0,1}
7	4	1	4	{3}	-{1,0}	{1,0,0,0,1}
7	4	1	5	{4}	-{1,0}	{1,0,0,0,1}
7	4	1	6	{5}	-{1,0}	{1,0,0,0,1}
7	4	1	7	{6}	-{1,0}	{1,0,0,0,1}
7	4	1	8	{7}	-{1,0}	{1,0,0,0,1}
7	4	1	9	{8}	-{1,0}	{1,0,0,0,1}
7	4	1	10	{9}	-{1,0}	{1,0,0,0,1}
7	4	1	11	{10}	-{1,0}	{1,0,0,0,1}
7	4	1	12	{11}	-{1,0}	{1,0,0,0,1}
7	4	1	13	{12}	-{1,0}	{1,0,0,0,1}
7	5	1	2	{1}	-{1,0,1,0}	{1,0,1,0,0,1}
7	5	1	3	{2}	-{1,0,1,0}	{1,0,1,0,0,1}
7	5	1	4	{3}	-{1,0,1,0}	{1,0,1,0,0,1}
7	5	1	5	{4}	-{1,0,1,0}	{1,0,1,0,0,1}
7	5	1	6	{5}	-{1,0,1,0}	{1,0,1,0,0,1}
7	5	1	7	{6}	-{1,0,1,0}	{1,0,1,0,0,1}
7	5	1	8	{1}	-{1,0,1,0}	{1,0,1,0,0,1}
7	5	1	9	{8}	-{1,0,1,0}	{1,0,1,0,0,1}
7	5	1	10	{9}	-{1,0,1,0}	{1,0,1,0,0,1}
7	5	1	11	{10}	-{1,0,1,0}	{1,0,1,0,0,1}
7	5	1	12	(11)	-{1,0,1,0}	{1,0,1,0,0,1}
7	5	1	13	{12}	-{1,0,1,0}	{1,0,1,0,0,1}
7	5	1	14	{13}	-{1,0,1,0}	{1,0,1,0,0,1}
		...	...	...	...	...
8	3	1	2	{1}	-{1,0}	{1,0,0,1,0,0,1}
8	3	1	3	{2}	-{1,0}	{1,0,0,1,0,0,1}
8	3	1	4	{3}	-{1,0}	{1,0,0,1,0,0,1}
8	3	1	5	{4}	-{1,0-}	{1,0,0,1,0,0,1}
8	3	1	6	{5}	-{1,0}	{1,0,0,1,0,0,1}
8	3	1	7	{6}	-{1,0}	{1,0,0,1,0,0,1}
8	3	1	8	{7}	-{1,0}	{1,0,0,1,0,0,1}
8	3	1	9	{8}	-{1,0}	{1,0,0,1,0,0,1}
8	3	1	10	{9}	-{1,0}	{1,0,0,1,0,0,1}
8	3	1	11	{10}	-{1,0}	{1,0,0,1,0,0,1}
8	3	1	12	{11}	-{1,0}	{1,0,0,1,0,0,1}
8	3	1	13	{12}	-{1,0}	{1,0,0,1,0,0,1}
	...	...	...	...	...	...
8	5	1	2	{1}	{1,0,0,1}	-{1,0,0,1,0,1,0}
8	5	1	3	(2).	{1,0,0,1}	-{1,0,0,1,0,1,0}
8	5	1	4	{3}	{1,0,0,1}	-{1,0,0,1,0,1,0}
8	5	1	5	{4}	{1,0,0,1}	-{1,0,0,1,0,1,0}
8	5	1	6	(5}	{1,0,0,1}	-{1,0,0,1,0,1,0}
8	5	1	7	{6}	{1,0,0,1}	-{1,0,0,1,0,1,0}
8	5	1	8	{7}	{1,0,0,1}	-{1,0,0,1,0,1,0}
8	5	1	9	{8}	{1,0,0,1}	-{1,0,0,1,0,1,0}
8	5	1	10	{9}	{1,0,0,1}	-{1,0,0,1,0,1,0}
8	5	1	11	{10}	{1,0,0,1}	-{1,0,0,1,0,1,0}
8	5	1	12	(И)	{1,0,0,1}	-{1,0,0,1,0,1,0}
8	5	1	13	{12}	{1,0,0,1}	-{1,0,0,1,0,1,0}
8	5	1	14	{13}	{1,0,0,1}	-{1,0,0,1,0,1,0}
8	5	1	15	{14}	{1,0,0,1}	-(1,0,0,1,0,1,0)
	...	...	...	...	...	...
10	6	2	2	(1,1)	-{1,0,0}	{1,0,0,0,0,0,1}
10	6	2	3	{2,2}	-{1,0,0}	{1,0,0,0,0,0,1}
10	6	2	4	{3,3}	-{1,0,0}	{1,0,0,0,0,0,1}
10	6	2	5	{4,4}	-{1,0,0}	{1,0,0,0,0,0,1}
10	6	2	6	{5,5}	-{1,0,0}	{1,0,0,0,0,0,1}
10	6	2	7	{6,6}	-{1,0,0}	{1,0,0,0,0,0,1}
id	6	2	8	(7,7)	-(1,0,0)	(1,0,0,0,0,0,1)
10	6	2	9	(8,8}	-(1,0,0)	(1,0,0,0,0,0,1)
10	6	2	10	(9,9)	-(1,0,0)	(1,0,0,0,0,0,1)
10	6	2	11	(10,10}	-(1,0,0)	(1,0,0,0,0,0,1)
10	6	2	12	(11,11}	-(1,0,0)	(1,0,0,0,0,0,1)
10	6	2	13	(12,12}	-(1,0,0)	(1,0,0,0,0,0,1)
10	6	2	14	(13,13}	-(1,0,0)	(1,0,0,0,0,0,1)
10	6	2	15	(14,14}	-(1,0,0)	(1,0,0,0,0,0,1)
10	6	2	16	(15,15}	-(1,0,0)	(1,0,0,0,0,0,1)
10	6	2	17	(16,16)	-(1,0,0)	(1,0,0,0,0,0,1)
10	6	2	18	(17,17)	-(1,0,0)	(1,0,0,0,0,0,1)
10	7	1	2	(1)	-(1,0,0,1,0)	(1,0,0,1,0,0,0,1)
10	1	1	3	(2}	-(1,0,0,1,0)	(1,0,0,1,0,0,0,1)
10	1	1	4	(3}	-(1,0,0,1,0)	(1,0,0,1,0,0,0,1)
10	1	1	5	(4}	-(1,0,0,1,0)	(1,0,0,1,0,0,0,1)
10	1	1	6	(5}	-(1,0,0,1,0)	{1,00, 1,0, 0,0,1}
10	1	1	7	(6}	-(1,0,0,1,0)	{1,0,10,1,0,0,0,1}
10	1	1	8	(7)	-(1,0,0,1,0)	{1,0,:0, 1,0, 0,0,1}
10	7	1	9	(8}	-(1,0,0,1,0)	{1,0,0,1,0,0,0,1}
10	7	1	10	(9)	-{1,0,0,1,0}	(1,0,0,1,0,0,0,1)
10	7	1	11	(10}	-(1,0,0,1,0}	(1,0,0,1,0,0,0,1)
10	7	1	12	(11)	-(1,0,0,1,0)	(1,0,0,1,0,0,0,1)
10	7	1	13	(12)	-(1,0,0,1,0}	(1,0,0,1,0,0,0,1)
10	7	1	14	(13)	-(1,0,0,1,0}	(1,0,0,1,0,0,0,1)
10	7	1	15	(14)	-(1, 0,0,1,0}	(1,0,0,1,0,0,0,1)
10	7	1	16	(15)	-{1, 0,0,1,0}	(1,0,0,1,0,0,-0,1)
10	7	1	17	(16)	-(1,0,0,1,0)	{1,0,0,1,0,0,0,1}
10	7	1	18	(17}	-(1,0,0,1,0)	(1,0,0,1,0,0,0,1}
10	7	1	19	(18}	-(1,0,0,1,0)	(1,0,0,1,0,0,0,1}
		...	...	...	...	...

Честно говоря, возникает желание избавиться от этого назойливого повторения. Как это сделать? Для этого придется переделать программу. Но чтобы программа не была слишком длинной, лучше переписать ее. Прежде всего, к уже имеющимся определениям

ааа[а_,n_]:=аАп-1; d:= GCD[n, m]

добавим еше два для печати.

prnt : = {Print["###",n, ":",m,":",d,":",a,":"],

If[g<0,Print["-"]],

Print[IntegerDigits[g,a],":"],

If[r<0,Print["-"]],

 Print[IntegerDigits[r,a],":"],

 If [s<0-. Print ["-"] ] ,

Print[ IntegerDigits [s, a] ] };

prnt1:={Print["%%%",n,":",m,":",d,":"],

If[r<0, Print["-"]],

Print[FromDigits!IntegerDigits[r,a],10],":"],

 If[s<0,Print!"-"]];

Print[FromDigits[IntegerDigits[s,a],10]]); 

Основным определением здесь является prntl. Именно это определение используется для первого вывода на печать значений n, m, d = НОД(n, m), а также двоичных представлений rus. Чтобы облегчить распознавание определения, которое выполняет печать, в основном определении (prntl) ведущими символами являются ###, а во вспомогательном (prnt) — %%%. Используя вспомогательное определение prnt, предыдущую программу можно переписать так.

Do[

Do[

Do[{{g,{r,s)}=ExtendedGCD[aaa[a,n],aaa[a,m]], prnt},

{a,2,n+m+2}], {m,n-l}], {n,10}] 

Вспомогательное определение prnt будет использоваться для первого вывода на печать только тех представлений г и s, которые отличаются от первого. Поэтому в этом определении предусмотрен вывод дополнительной информации: представления g и основания системы счисления а.

Теперь программу можно модифицировать с учетом нового определения функции печати. Возникает соблазн написать программу так.

Do[

Do[{

Do[{{g,{r,s}}=ExtendedGCD[aaa[a,n],aaa[a,m]],

 If[a==2,{{g0,{r0,s0}}={g,(r,s)}, prntl}],

 If[{g0,{r0,s0}}!={g,{r,s}},prnt]},{a,2,n+m+2}]},{m,n-l}],{n,10}] 

Но это совсем не то, что мы хотели! Ведь условие {g0, {r0, s0}} ! = {g, {r, s}} будет выполнено при а! =2. Все дело в том, что значения ms зависят от основания системы счисления а\ Не зависит от основания системы счисления а лишь их представление в системе счисления с основанием а. Поэтому проверять нужно именно неизменность представления в системе счисления с основанием а. Кроме того, проверка g0! =n лишняя. Поэтому лучше добавить еще одно определение.

newrs:= 

{ Signfr0], Signts0], IntegerDigits[r0,2],

 IntegerDigits[s0,2] } != { Sign[r], Sign[s],

IntegerDigits[r, a], IntegerDigits[s, a] } 

Теперь можно записать программу.

Do[

Do [{

Do[{{g,{r,s}}=ExtendedGCD[aaa[a,n],aaa[a,m]],

 If[a==2,{ {r0,s0}={r,s}, prntl}], If[newrs,prnt]}, 

{a,2,n+m+2H }, {m,n-l} ]; {n,20}] 

Теперь выполним программу. Сколько раз сработала вспомогательная печать? Ни разу! Это значит, что по всем найденным значениям г и s можно восстановить многочлены г(х) и s(x) и написать тождество d(x) = r(x)a(x)+s(x)b(x)\ Полученные результаты стоят того, чтобы собрать их в таблицу (табл. Б.33).

Полученная таблица заслуживает более внимательного рассмотрения. Рассмотрим, например, одну строку таблицы.

20

17

1

1001001001001001

-1001001001001001010 |

Так как d(x) = xd -I = лс-1, эта строка означает, что х-1 = d(x) = r(x)a(x)+s(x)b(x), где а(х)= JC20-1, 'b(х) = хⁿ-1, r(х) = 1+x³+x⁶+х⁹+x¹²+x¹⁵, s(x) =-(х+х³+ х⁶+x⁹+х¹²+ х¹⁵+х¹⁸). Иными словами, она означает, что х-1 = d(x) =r(х) (х²⁰ -1) +s(x) (хⁿ -1) для указанных только что полиномов г(х) и s(x).

Впрочем, вместо r(x) и s(x) можно подставить их выражения, и тогда получится следующее тождество:

x-1 = (1+х³+x⁶+x⁹+x¹²+x¹⁵) (х²⁰-1) -(х+х³ + х⁶+х⁹ + х¹²+х¹⁵ +х¹⁸) (х¹⁷-1).

Таким образом, мы видим, что каждая строка полученной таблицы фактически основана на полиномиальном тождестве и фактически является кратким его кодом!

Давайте теперь сравним полученные значения для г и s в равенстве НОД(a, b) = ra+sb для а = х^n-1 -1, b= х^m+1 -1 (х целое) с теми, которые были получены ранее для такого же равенства для чисел а и b, десятичная запись которых состоит из т единиц и n единиц. (Нужную таблицу мы подготовили заранее.) Не случайно ли значения г и s совпадают? Нет, не случайно. Дело в том, что если справедливо равенство НОД(а,- b) = ra+sb для а = х^n-1 -1, b = x^m+1 -1 (х целое, отличное от 1), то справедливо и равенство  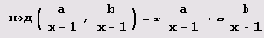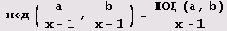. (Напомню, что числа    целые при целом х  и а = хⁿ⁺¹ -1, b = x^m+1 -1.) Более того, запись чисел в системе счисления  с целым основанием х как раз и состоит из n единиц и m единиц. Поскольку равенства НОД(а, b) = ra+sb и  ⁿ⁺¹-1, b= х^m+1-1 (х целое, отличное от 1) равносильны, то г и s принимают в них одинаковые значения. Отсюда, в частности, следует, что если числа r и s из равенства НОД(а,b) = ra+sb имели одно и то же представление для любого основания системы счисления х, то же самое будет справедливо и для чисел r и s из равенства 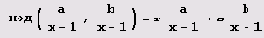 ⁿ⁺¹-1, b= х^m+1-1,  ⁿ⁺¹ -1 и b = x^m+1 -1, фактически отличаются только множителем х-1. Например, из тождества  x-1 = (1+х³+x⁶+x⁹+x¹²+x¹⁵) (х²⁰-1) -(х+х³ + х⁶+х⁹ + х¹²+х¹⁵ +х¹⁸) (х¹⁷-1).  получается еще более длинное тождество:

1 =x-1 = (1+х³+x⁶+x⁹+x¹²+x¹⁵) (х²⁰-1) -(х¹⁹ + х¹⁸+х¹⁷ +...+х+1) -(1+х³+x⁶+x⁹+x¹²+x¹⁵+x¹⁸) *(х¹⁶ + х¹⁵+х¹⁴ +...+х+1)

Обратите, наконец, внимание на то, что в полученной таблице представления чисел r и s содержат только нули и единицы. Это означает, что коэффициенты полиномов r(х) и s(x), построенных по представлениям чисел r и s, тоже будут равны 0 и 1 (либо - 1, если перед представлением стоит знак минус).

Наименьшее общее кратное — функция LCM Во множестве всех кратных нескольких данных чисел всегда найдется такое, которое является делителем всякого другого общего кратного этих чисел: это — общее наименьшее кратное. Функция LCM находит наименьшее общее кратное в области целых, рациональных и гауссовых чисел. Что такое наименьшее общее кратное нескольких рациональных чисел? Это, конечно, такое наименьшее рациональное число, частные от деления которого на данные рациональные числа являются целыми. Пример 6.11. Наименьшее общее кратное первой тысячи чисел. Вот как можно его найти. Это, конечно же, существенно меньше, чем 1000!. В раз! Заметьте, что наименьшее общее кратное первой тысячи чисел заканчивается всего лишь четырьмя нулями. Пример 6.12. Графики функции LCM. Давайте теперь построим несколько графиков функции LCM. Поскольку это функция двух аргументов, построим изображения поверхности z = LCM[IntegerPart [x], IntegerPart [у] ]. Для этого используем функцию Plot3D. А вот вид вблизи.

Задача нахождения наибольшего общего делителя

Задача нахождения наибольшего общего делителя и наименьшего общего кратного нескольких чисел столь важна, что ее приходится решать практически постоянно. Даже занимаясь решением задач вариационного исчисления, математической физики, линейной алгебры, математического анализа, аналитической геометрии или просто решая какие-нибудь дифференциальные уравнения, вам практически не удастся избежать сложения или вычитания дробей — действий, которым учатся в пятом классе. И как только вам приходится выполнять эти действия, вы так или иначе вспоминаете о наибольшем общем делителе и наименьшем общем кратном. К счастью, система Mathematica если и не позволяет забыть об этих двух важнейших понятиях арифметики, то избавляет вас от рутинной работы по их нахождению. В системе Mathematica реализованы весьма эффективные, вполне современные алгоритмы нахождения наибольшего общего делителя и наименьшего общего кратного. Пользуясь ими, вы можете быть уверены, что используете самые современные инструменты. Конечно, их применение целиком зависит от вас. Вы можете составить таблицы, найти тождества, решить неопределенные уравнения...

---

---