Частное при делении с остатком — функция Quotient

Чтобы получить частное при делении (с остатком) л на т, нужно воспользоваться функцией Quotient [n,m]. Рассмотрим пример.

Quotient [16,5] 3

Для целых n и m выражение Quotient [n,m] равносильно Floor [m/n]. Однако n и т могут быть вещественными и даже комплексными числами.
Quotient[Е^10,ЕЛ8] 7 Quotient[Е^10+25*1,Е^8+41]

7-1
В случае вещественных чисел Quotient [n, m] — это такое целое число х, что d<n-m х<d+m. Однако часто нужно найти целое число х, такое, что d<n-m x<d+m. Пожалуйста, укажите сдвиг d третьим параметром.

Quotient[16,5,14]

0

Вот как можно найти частные от деления чисел 0, 1, 2, ..., 21 на 3.

Quotient[Range[0,21],3]

{0,0,0,1,1,1,2,2,2,3,3,3,4,4,4,5,5,5,6,6,6,7}

А вот частные, когда задан сдвиг 1.

Quotient[Range[0,21],3,1]

{-1,0,0,0,1,1,1,2,2,2,3,3,3,4,4,4,5,5,5,6,6,6}

А вот частные, когда задан сдвиг 2.

Quotient[Range[0,21],3,2]

{1,-1,0,0,0,1,1,1,2,2,2,3,3,3,4,4,4,5,5,5,6,6}

Пример 7.1. Графики функции Quotient.

Давайте теперь построим несколько графиков функции Quotient. Поскольку это функция двух аргументов, построим изображения поверхности z = Quotient [х, у]. Для этого используем функцию plot3D.

А вот вид вблизи.

Остаток от деления — функция Mod

Чтобы получить остаток от деления n на m, нужно воспользоваться функцией Mod[n,m]. Наименьший возможный остаток в этом случае равен нулю, а наибольший... Как вы думаете, чему равен наибольший возможный остаток? "Конечно, m-1", — возможно, подумали вы. Ну, что же, я, конечно, приветствую ваши глубокие познания в теории чисел, ибо именно так написано во всех классических учебниках по этой дисциплине, если, конечно, именно в этом месте нет какой-либо досадной опечатки. Но должен вас разочаровать: вы не угадали. Зато, надеюсь, вам будет приятно узнать, что возможности функции Mod значительно шире, чем требуется для решения задач из задачников по классической теории чисел. Дело в том, что аргументы этой функции могут быть не только целыми (это предусмотрено классическими учебниками теории чисел), но и вещественными и даже комплексными! А во множестве вещественных чисел, как вы, надеюсь, еще помните, полно сюрпризов... Но сначала давайте рассмотрим простейший случай целых аргументов.

Mod[7,5]

2

Ну вот, при делении 7 на 5 остаток равен 2. Просто и понятно, даже в уме можно вычислить. Вот еще один пример.

Мод[3^10,5]

4

Тоже в уме, и тоже просто и понятно. Но вот несколько примеров с вещественными числами.

Теперь, надеюсь, вы поняли, что множество значений Mod[n,m] не имеет набольшего элемента. Можно лишь утверждать, что при вещественных m и n 0<Mod [n, m] <m, причем все значения из открытого справа интервала [0, m) функция Mod[n,m] принимает. Но иногда нужно сдвинуть этот интервал на d. Нет проблем: укажите сдвиг d третьим параметром.

Вот как можно найти остатки от деления чисел 0, 1,2, ..., 21 на 3.

Mod[Range[0,21],3]

{0,1,2,0,1,2,0,1,2,0,1,2,0,1,2,0,1,2,0,1,2,0}

А вот те же остатки, когда задан сдвиг 1.

Mod[Range[0, 21] ,3,1]

{3,1,2,3,1,2,3,1,2,3,1,2,3,1,2,3,1,2,3,1,2,3}

А вот те же остатки, когда задан сдвиг 2.

Mod[Range[0,21],3,2]

{3,4,2,3,4,2,3,4,2,3,4,2,3,4,2,3,4,2,3,4,2,3}

Ниже приведены основные свойства функций Quotient и Mod:

n*Quotient[m, n, d] + Mod[m, n, d] = m при любых допустимых m, n, d; знак Mod [m, n] совпадает со знаком и при любых допустимых вещественных m, n; Mod[m, n] = m-n*Quotient [m, n] при любых допустимых m, n; Mod [m, n, d] = m-n*Quotient [т, n, d] при любых допустимых m, n, d; Mod[x, 1] равно дробной части х

Ну и, наконец, полезно иметь в виду, что аргументы функции Mod могут быть списками. Это, например, позволяет найти остаток от деления данного числа сразу на несколько чисел.

Mod[244, {4, 9, 121}]

{0,1,2} ,

Можно также найти остатки от деления нескольких чисел на заданное число.

Mod[{0,l,2,3,4)A2,5]

{0,1,4,4,1}

Пример 7.2. Графики функции Mod.

Теперь давайте построим несколько графиков функции Mod. Поскольку это функция двух аргументов, построим изображения поверхности z = Mod[x, у]. Для этого используем функцию Plot3D.

А вот вид вблизи.

Возведение в степень в модулярной арифметике — функция Power Mod

Иногда приходится решать задачи такого типа:

найти вычет а^b по модулю n; найти последние m цифр числа а^b в системе счисления с основанием с.

Конечно, совсем несложно написать что-нибудь вроде Mod[a^b,n] или Моd[а^b, с^m]. Однако все дело в том, что в исследовательских задачах b может быть столь велико, что для вычисления а^b не хватит памяти. Кроме того, по мере вычисления а^b часто бывает так, что требуется все больше памяти и начинает работать подкачка, что очень часто приводит к пробуксовыванию. А тогда процессор практически простаивает, и даже самая простая операция выполняется фантастически долго.

Пример 7.3. Наибольшее число, которое можно записать тремя цифрами. Число 9⁹⁹ имеет 369 693 100 цифр, т.е. более трети миллиарда! Еще в 1953 году было известно, что это число начинается цифрами 428 124 773 175 747 048 036 987 115 930 563 521 339 055 482 241 443 514 174 753, а заканчивается цифрами 24178799359681422627177289. Какие цифры между ними, не было известно и в 1959 году. Ведь если это число напечатать более или менее четко на полоске бумаги, то эта полоска оказалась бы длиной 1200, а может и 1800 км. Если же напечатать это число в книге так, чтобы на каждой странице помещалось 14 000 цифр (на странице обычно помещается 2,5—3 тысячи знаков), то такая книга состояла бы из 33 томов по 800 страниц в каждом. Но с помощью системы Mathematica несложно вычислить, например, первую и последнюю тысячу цифр числа 9⁹⁹. Чтобы вычислить первую тысячу цифр числа 9⁹⁹, нужно просто вычислить это число с разрядностью не менее тысячи знаков. Вот как это делается.

М[9^(9^9),1000]

 4.281247731757470480369871159

30563521339055482241443514174753723053523

887471735048353193665299432033375060417533

64763100078032613904733860832080206037470612

809165574132086446019861999614520310524428581489598115

 1471949351767796559302159393385015023969426231

0529675816569433334631474925538494859337781208762

495721650419522060180457130151786405101459407

904194866332733667183065441076023482363342793388473

449171490713928387636703470733221615842638847026446

505858035582482311577827786618011472099436290690473438

366488664695023381735331493288811517612485971201533575

64439876059956217339548503950536965544532955477621833381

799037537429866036175410766960904718339923933145342547022

698333065128258703520736236 343330809161939992399143539

9517426262619225044491488935534629633876424,

710803619094832833935338326811681684096752173716022

71240386424109448631241673361631602584738577273169933875

567294188775379238762791518151971 69574861839692092170993

60780264476440839592643445485180078094839593328

539827016475025109538Х10^369693099

Почти так же можно вычислить и последнюю тысячу знаков.

Mod[9^(9^9),10^1000]//Timing

{260.64 Second,

164378947574778447311427807670372670

0326359025082234292387746462391127

9751529028988405927046285969119001418

842032015433264756391857718597649 204912230323811027210136918

3684943285741373762637969125845614123744406 01020026085922354

10622770718702230402359356419151296996286668460066302 9835137

9027215796574565344432784903341994543575575416975966278964106

12 7038799025612835366795058993611717249028581457173391518760

2283281383558665788995350272253954345165983917336427507154331

749386377957650223307 168958637197192110578737857336943212457

7155212755139983177854767167859 12996450672962748373653022152

34320507478340927905653712738326405359097 6996351343597753799

283680752817548382724478144536940979972304718417625 894479515

4018072624283659761429188348967918815377285476781074966161266

1854762666853235529005571888491679885547006847358268508973918

700851075402818853925349052912288203971972

4032235787006073283877358282

617004315060225040660196165699439754361026855266374036682906

1901749234943241787 99359681422627177289}

Вычисление, как видите, заняло более четырех минут (260,64 секунды). Но гораздо быстрее результат можно получить вот так.

PowerMod[9,9^9,10^1000]//Timing

{0.015 Second, 1643789475747784473114278076703726700...2627177289}

(Здесь середина пропущена.) Это вычисление заняло лишь 0,015 секунды. Это более чем в тысячу (точнее, в 17376) раз быстрее!

Пример 7.4. Графики функции Power Mod.

Давайте теперь построим несколько графиков функции PowerMod. Поскольку это функция двух аргументов, построим изображения поверхности z = PowerMod[x, у]. Для этого используем функцию Plot3D.

А вот вид издалека.

Китайская теорема об остатках — функция ChineseRemainder

Хитрый китаец Сунь Цю около 2000 лет назад (конечно, это могло быть и 200 лет до нашей эры, и 200 лет после начала нашей эры) открыл правило "гай-йен" ("большое обобщение"), которое является частным случаем целочисленного аналога интерполяционной формулы Лагранжа для полиномов. (Правда, примерно в то же самое время, в 100 г. н. э., греческий математик Никомах знал точно тот же частный случай.) Полностью формула была сформулирована и доказана впервые, по-видимому, в 1734 году Л. Эйлером. Сформулируем китайскую (или греко-китайскую, как назвал ее Акритас, автор одного из широко известных учебников по компьютерной алгебре?) теорему об остатках и укажем соответствующее правило (формулу).

Пусть m₁, m₂, ..., m_r — попарно взаимно простые модули (попарно взаимно простые положительные целые числа), m = m₁, m₂, ... m_r — их произведение, а а, u₁, u₂, ..., u_r — произвольные целые числа. Тогда существует ровно одно целое число и, такое, что а<u<а+m, удовлетворяющее всем сравнениям u = u_i(modm_i). Более того,

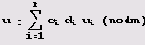
где c_i — произведение всех модулей, кроме m_i: с_i = m/m_i, a _di=c_i^-1 (modm_i) (т.е. d_ic_i = 1(modm_i)).

Эта теорема имеет многочисленные применения в математике, информатике (машинная арифметика) и криптологии (секретные ключи). Для нахождения числа и, существование которого гарантировал хитрый китаец Сунь Цю, в пакете теории чисел существует "китайская" функция ChineseRemainder. ChineseRemainder [список_1, список_2] — это такое наименьшее целое неотрицательное число и, что Mod [и, список_2] = список_1. Чтобы ею воспользоваться, нужно сначала загрузить пакет теории чисел.

<<NumberTheory`NumberTheoryFunctions`

После загрузки пакета можно вызвать эту функцию.

ChineseRemainder[{0,1,2), {4, 9,121}]

244

Полученный ответ означает, что 244=0(mod4), 244=1(mod19) и 244=2(mod121)-С помощью функции Mod это легко проверить.

Mod[244,{4,9,121}]

{0,1,2}

Пример 7.5. "Задача о корзинке с яйцами". Есть одна очень старая задача, в которой используется китайская теорема об остатках. Вот современная формулировка задачи. Крестьянка (наверняка отличница местной школы, а может даже победительница олимпиад по поднятию тяжестей) несла по проселочной дороге на базар яйца. Однако по дороге очень быстро ехал экипаж с сеньором, и экипаж нечаянно зацепил корзинку, в которой были яйца. Корзинка опрокинулась, и яйца разбились. Сеньор пожелал возместить убытки и спросил, сколько яиц было в корзинке. Крестьянка ответила, что не помнит, однако вспомнила, что когда вынимала яйца парами, то оставалось одно яйцо, когда тройками, то — два яйца, когда семерками — то 6 яиц и, вообще, когда она вынимала по p_i(p_i — i-e простое число) яиц, то в корзинке оставалось ровно i яиц. И еще вспомнила, что так она делала для всех первых ста простых чисел. Спрашивается, какое наименьшее число яиц могло быть в корзинке. С помощью функции ChineseRemainder это число можно найти так.

Ну и корзинка, которая вмещала столько яиц!

Корни в системе остаточных классов

Задача о корзинке с яйцами представляет собой задачу о решении системы сравнений вида u=u_i(modm_i) с попарно взаимно простыми модулями mt. Конечно, она

допускает дальнейшие обобщения. Если не считать линейных сравнений и их систем, то наиболее простой из таких задач окажется задача об извлечении квадратного корня в системе остаточных классов, т.е. задача о решении сравнения хr = d (modn).

Квадратный корень по модулю — функции SqrtMod и SqrtModList

Конечно, квадратных корней в системе остаточных классов — решений сравнения х =d (mod n) — может быть более одного. Поэтому в системе Mathematica предусмотрено две функции для нахождения таких решений. Функция SqrtMod находит наименьший вычет, а функция SqrtModList — Список всех вычетов.

Наименьший квадратный корень по модулю — функция SqrtMod

Выражение SqrtMod[d, n] представляет собой наименьший неотрицательный квадратный корень из d по модулю n, т.е. такой наименьший неотрицательный вычет m, что m2sd(modn). Но это, конечно, в том случае, если такое т существует. Для этого d, понятно, должно быть полным квадратом по модулю и, т.е. символ Якоби .jacobiSymbol [d, n] должен быть равным 1. Это условие также достаточно, если и является простым числом. Для простых n система Mathematica использует алгоритм Шенкса (Shanks). Для примера найдем самое маленькое неотрицательное целое число, такое, что его квадрат равен 3 по модулю 11.

SqrtMod[3,11] 5

Этот результат легко проверить.

Mod[Range[11]^2,11]

{1,4,9,5,3,3,5,9,4,1,0}

Как видите, только квадраты чисел 5 и 6 по модулю 11 равны 3. Если квадратный корень из d по модулю п не существует, SqrtMod [d, n] останется невычисленным.

Убедимся, например, что квадратный корень из 3 по модулю 5 не существует.

Mod[{0,l,2,3,4}*2,5]

{0,1,4,4,1}

Ну и, конечно, нельзя не пройти мимо вычисления квадратного корня из 2.

SqrtMod[2,1СГ64+57]//Timing

{0.016

Second,876504467496681643735926111996546100401033611976777074909122865 }

Функция SqrtMod может вычислять квадратные корни не только по простому модулю, но и по составному.

Однако не всегда такие вычисления происходят мгновенно. Для вычисления квадратного корня приходится разлагать модуль на множители, и потому для очень больших составных модулей функция SqrtMod далеко не всегда дает результат.

Список всех квадратных корней по модулю — функция SqrtModList

Как мы только что видели, квадратных корней может не быть совсем, а может быть несколько. Список всех квадратных корней из данного числа по заданному модулю дает функция SqrtModList. Если квадратных корней нет, список, естественно, будет пустым. Вот пример, когда существует два квадратных корня.

SqrtModList[3,11]

{5,6}

А вот пример, когда квадратных корней нет совсем.

SqrtModList[2,11]

{}

Существование квадратного корня по модулю и символ Якоби — функция JacobiSymbol

Как узнать, существует ли квадратный корень из данного числа d по модулю и? Иногда для этого достаточно вычислить символ Якоби

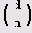
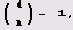го d является квадратичным невычетом по модулю d. Если же Якоби

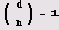
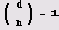то о квадратичности вычета d по модулю и судить непосредственно нельзя.) Для вычисления символа Якоби в системе Mathematica предусмотрена функция JacobiSymbol [d, n]. Число 2 не является квадратичным вычетом по модулю 13, а число 4 является таковым (по любому модулю).

{JacobiSymbol[2,13],JacobiSymbol[4,13]}

{-1,1}

Первообразные корни по модулю n

Показатели — функция MultiplicativeOrder

Наименьшее натуральное решение т показательного сравнения km =1(modn) называется показателем числа k по модулю п. (Иногда это выражают иначе: говорят, что k принадлежит показателю т по модулю n.) В этом случае можно сказать, что k является корнем m-й степени из единицы в кольце классов вычетов по модулю т. Вот пример: 2 принадлежит показателю 4 по модулю 5.

Table[Mod[2го, 5], {m, 10}]

{2,4,3,1,2,4,3,1,2,4}

Для вычисления показателя т в системе Mathematica предусмотрена функция

MultiplicativeOrder[k, n].

MultiplicativeOrder[2,5] 4

Конечно, показатели существуют не во всех случаях, а только тогда, когда k ч п взаимно просты. Если показатель не существует, функция MultiplicativeOrder [k, n] остается невичисленной.

Функция MultiplicativeOrder может иметь еще третий параметр — список. Список {а,, а,,..., as} в вызове MultiplicativeOrder [k, n, {а,, а,, ..., as } ] используется тогда, когда нужно найти наименьшее т, удовлетворяющее хотя бы одному из сравнений km =a, (mod/i). 3 является наименьшим натуральным числом, удовлетворяющим хотя бы одному из сравнений 2m =5 (mod n) и 2^m =8(modn).

Table[PowerMod[2,m,11],{m,10}]

{2,4,8,5,10,9,7,3,6,1}

Вот как это можно вычислить.

MultiplicativeOrder[2,11,{5,8}]

3

Пример 7.6. Длина периода систематической дроби по основанию b. Вот функция, которая вычисляет длину периода систематической дроби, представляющей рациональное число r по основанию b.

DigitCycleLength[r_Rational,b_Integer?Positive]:=

MultiplicativeOrder[b,FixedPoInt[Quotient[#,GCD[#,b]]&,

Denominator[r]]]

Вот пример. Длина периода дроби 1/49 в десятичной системе равна 42.

DigitCycleLength [1/4.9,10]

42

А вот и подтверждение.

N[1/49,151]

0.020408163265306122448979591836734693877551

020408163265306122448979591836734693877551

020408163265306122448979591836734693877551

02040816326530612244897959

Что такое первообразный корень по модулю n

Решая сравнение k_m =l(modn) относительно k, можно заметить, что при некоторых n находятся такие k, которые принадлежат довольно большим показателям m. В частности, при некоторых n случается, что k принадлежит показателю, который равен числу вычетов, взаимно простых с n. Такие числа k называются первообразными корнями по модулю n. Конечно, по составному модулю в большинстве случаев первообразных корней не существует. Первообразные корни существуют только по модулям 2, 4, рⁱ и 2 рⁱ(здесь р — произвольное нечетное простое число). Для вычисления первообразных корней по модулю и в системе Mathematica предусмотрена функция PrimitiveRoot [n].

PrimitiveRoot[5]

2

Если первообразного корня не существует, функция остается невычисленной.

PrimitiveRoot[11*13] PrimitiveRoot[143]

Следует помнить, что PrimitiveRoot использует Factorinteger как подпрограмму, так что она может не справиться с вычислениями в случае очень большого параметра.

Критерии простоты чисел специального вида

Рассмотренные числовые функции могут успешно применяться для проверки простоты чисел специального вида. С помощью числовых функций для чисел специального вида удается построить критерии, эффективность которых часто на несколько порядков выше, чем эффективность критериев для чисел произвольного вида. Данная тема необъятна, и ниже рассмотрены только самые простые примеры применения таких критериев.

Простые числа Мерсенна, тест Люка-Лемера

Наибольшее простое число поймано решетом Эратосфена.

Конечно, решето Эратосфена годится для поиска простых чисел Мерсенна не более чем консервная банка для плавания через Атлантический океан. Гораздо более пригодна для этой цели функция PrimeQ. С ее помощью мы нашли все те индексы простых чисел Мерсенна, которые не превышают 5000. Дальнейшее продвижение оказалось практически невозможным. Однако есть другой метод проверки простоты чисел этого вида. Его опубликовал Э. Люка (Lukas2) в 1878 году, а в 1930 году усовершенствовал Д. X. Лемер. Он основан на следующей теореме.

Если р>2 — простое число, то число Мерсенна Мр = 2^p -1 является простым тогда и только тогда, когда bр_r = О, где последовательность L; определяется так:

L0 =4, Lⁱ⁺¹=(L_i²-2)mod(2ⁱ-l).

Совершенно элементарное доказательство этой теоремы имеется во многих книгах; в частности, его можно найти во втором томе трехтомника Кнута. Чтобы сократить доказательство, можно также заметить, что критерий Люка основан на малой теореме

Ферма для чисел из полей Q(√5) или Q(v3). Тест Люка позволил проверить вручную все простые числа до МР7. Когда для проверки простоты стали применяться ЭВМ, началась настоящая гонка. Очередные новые простые числа Мерсенна рассматривались как свидетельство быстрого роста возможностей ЭВМ. Чтобы убедиться, что Л/819] является составным, Д. Дж. Уилер потратил около 100 часов машинного времени ILLIAC I — самой быстрой ЭВМ выпуска пятидесятых годов. Гурвицу на IBM 7090 для этой же цели потребовалось лишь 5 часов в 1962 году. В 1964 году Гиллис сделал это на ILLIAC II за 49 минут. А в 1971 году Такерман потратил на это только 3 минуты на IBM 360/91. (Но то были суперЭВМ, а я на своем весьма слабеньком ПК на это потратил 4,125 секунды.) Проверка простоты М1тз на ILLIAC II заняла 2 часа 15 минут, и всего лишь 8 минут на IBM 360/91. (Но это столько нужно суперЭВМ, а моему старенькому ПК нужно всего лишь 9,672 секунды.) Найденное очередное простое число Мерсенна становилось визиткой фирмы. Например, доказательству простоты числа

М112,з Иллинойский университет посвятил выпуск фирменного конверта. IBM в долгу не осталась: она выпустила конверт, посвященный доказательству простоты М19937 (это 6002-значное число, найденное Б. Такерманом 4 марта 1971 года, довольно долго было рекордсменом). Проверка простоты этого числа и у меня заняла изрядное время - 42 094 секунды. с помощью функций Mod и powerMod несложно запрограммировать тест Люка- Лемера. Сначала дадим нужные определения.

Mn[n_]:=Module[{t=4}, Do[t=Mod [PowerMod[t, 2,mn] -2,mn],<i,

n}];   t];

MPrime[p_]:=Mn[p-2,Mn[p]]==0;

Поскольку единственным простым числом Мерсенна Мр с четным индексом р является Я,, можем ограничиться поиском только нечетных индексов р. (Конечно, программа при этом пропустит число Мг = 3, но разве мы можем о нем забыть?) Вот нужная нам программа поиска нечетных индексов р простых чисел Мерсенна М „.

Block[{p=3}, While [p<45000, {If[MPrime[р],Print[p]], p=NextPrime[p] } ] ]

Даже на весьма слабеньком компьютере всего за несколько часов вы можете найти все нечетные индексы р первых 24 простых чисел Мерсенна известных до 1980 года: 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423, 9689, 9941, 11213, 19937. Здесь, конечно, только 23 числа, поскольку индекс первого простого числа Мерсенна М2 = 3 четный: р = 2.

Надеюсь, вы о нем не забыли, так что не забудьте и отпечатать специальные конверт. Заметьте что данную программу очень легко распараллелить и организовать поиск на нескольких ЭВМ. Кроме того, данную программу легко модифицировать так, чтобы поиск продолжался после уже проверенных чисел. Впрочем, возможно, программу придется модифицировать так, чтобы она время от времени подавала признаки жизни", даже если не успевает найти простое число Мерсенна. Это можно сделать, например, так.

Block[{р=19937,1=1},p;

While   [p<45000,

 {If [MPrime [p],

Print [p]],

p=NextPnme [p] , If[Mod[i++,500]==0,

 Print["***p=",p]] HI

Так что если не поленитесь потратить ночку-другую на вычисления, то найдете и другие простые числа р, при которых р-е число Мерсенна Mf = 2'-l является простым. В частности, вы сможете найти 6533-значное простое число Мерсенна Л/,,70, (найдено калифорнийскими школьниками Никкелом и Ноллом в 1978 году), 6987-значное простое число Мерсенна М23209 (найдено Ноллом), 13395-значное простое число Мерсенна Мш„ (это 27-е простое число Мерсенна найдено Д. Словинским в 1979 году), 25962-значное простое число Мерсенна М86243 (это число Мерсенна найдено Дэвидом Словинским в январе 1983 года). Если хотите, проверьте, не пропустил ли я чего-нибудь и сможете ли вы продвинуться дальше. У меня проверка простоты М,1701 заняла 53,547 секунды, М2Ш) - 64,25 секунды, Мшу, - 350,562 секунды (ого, почти 6 минут!), Мим - 1845,34 секунды (это чуть больше получаса). Думаю, что дальнейшее продвижение по данной программе весьма затруднительно. В данном случае либо нужен компьютер со значительно более высоким быстродействием, либо нужно изменить программу так, чтобы большинство составных чисел отсеивалось еще до применения критерия Люка. Казалось бы, перед применением критерия Люка можно проверить, что число Мр не удовлетворяет сравнению ам' = a(modMp) при некоторых а. В качестве а удобно взять, например, число 3. Можно было бы также попытаться проверить другое свойство простых чисел. Однако при этом нужно тщательно следить за тем, чтобы все эти дополнительные проверки не снижали быстродействие программы. Время проверки сравнения aⁿ s=a(modMp) может оказаться, например, примерно равным времени проверки по критерию Люка—Лемера. Тогда, понятно, такая дополнительная проверка только замедляет выполнение программы. Так что дальнейшее продвижение требует изобретательности.

Дальше идет степень 110503. В 1983 году была найдена степень 132049, а в 1984 — 216 091. Поиском степеней на суперкомпьютерах прославился в 90-х годах XX столетия Дэвид Словинский. Вместе с Полем Гейджем он получил следующие индексы простых чисел Мерсенна: 756 839, 859 433, 1 257 787. Но степени 1 398 269 и 2 976 221 были найдены Жоэлем Арменгодом (Joel Armengaud) и Гордоном Спенсом (Gordon Spence) на персональных компьютерах по программе, разработанной Георгом Вольтманом (George Woltman) в 1996 году. Предварительная проверка Л/2,76,,, на компьютере с процессором Pentium с тактовой частотой 100 МГц заняла 15 суток в августе 1998 года! 27 января 1998 года Роланд Кларксон (Roland Clarkson) обнаружил простоту Л/3021377, а 1 июня 1999 года Найян Хьяратвала (Nayan Hayratwala) — простоту Af6972593. Впрочем, люди стремятся к рекордам, и после 1983 года числа проверялись не подряд, так что могли что-то и пропустить! Правда, добровольцы тщательно потом все просмотрели до миллиона!

Как из этого видно, критерий Люка—Лемера применяется только после некоторого предварительного отбора, которому уделяется огромное внимание. Давайте попробуем найти хотя бы какой-нибудь очень простой (а, значит, и довольно грубый) метод отсева показателей р, для которых числа Мерсенна Мр не являются простыми. Пусть s— показатель 2 по некоторому простому модулю q: Т =1 (mod q). (Такое 5 можно найти с помощью функции MultiplicativeOrder [2, q].) Поскольку Мp = 1ⁿ -1 оно делится на простое число q, если р является показателем 2 по простому модулю q. Так что такие индексы р чисел Мерсенна можно отсеять сразу, если Мр # q. Поэтому для предварительного отсева нам понадобится таблица показателей 2 по простым модулям q. Причем, чтобы уменьшить таблицу, из нее можно вычеркнуть все составные показатели. Чтобы построить таблицу, нам понадобится следующая функция.

f[n_]:=

Block[{q=  Prime[n],

s=MultiplicativeOrder[2,q]},

If[NumberQ[s],If[PrimeQfs],s]]]

Эта функция по заданному номеру n находит простое число q = рn, а затем — 5 (показатель 2 по найденному простому модулю q, если он существует). Если оказывается, что показатель 2 по простому модулю q существует, проверяется, является ли он простым числом. Если оказывается, что найденный показатель 2 по простому модулю q является простым числом, он возвращается в качестве значения функции. (В противном случае функция возвращает Null.) С помощью этой функции легко строится нужная нам таблица простых показателей 2 по простым модулям q.

t=Union[Sort[DeleteCasestArray[£,100000, 4] ,Null]]] ;

Функция Array [f, 100000, 4] генерирует следующий список из 100000 элементов {f[4], f[5],...}- Функция DeleteCases [Array [f ,100000, 4] ,Null] удаляет из него элементы, равные Null. Затем функция Sort сортирует этот список, а функцияUnion рассматривает его как множество и тем самым исключает из него повторяющиеся элементы.

Из массива, который первоначально содержал сто элементов, получается список всего из 15 элементов.

tl=Union[Sort[DeleteCases[Array[f,100,4],Null]]]

{3,5,7,11,23,29,37,43,73,83,131,179,191,239,251}

Понятно, что это очень мало. Но даже если бы мы исходили из тысячи простых чисел, у нас бы получился список из 80 элементов.

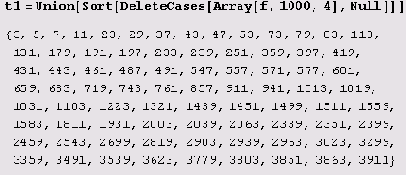
Если же взять сто тысяч простых чисел, получится список из 4536 элементов. Конечно, это тоже не очень много. Кроме того, не все элементы этого списка годятся для отсеивания. Не годятся, например, р = 3, 5, 7. Ведь если простое число р попало в нашу таблицу, это означает лишь, что М р делится на некоторое простое число, возможно на себя, — и тогда оно является простым числом! Поэтому для отсеивания пригодны лишь те элементы нашей таблицы, для которых Л/ больше самого большого простого модуля q, использованного для построения нашей таблицы. Правда, число Мерсенна Мр растет гораздо быстрее, чем л-е простое число рп. Поэтому для большинства элементов из полученного списка выполняется неравенство Мр >q, где q — самый большой простой модуль, использованный для построения нашей таблицы. Однако проблема заключается в том, что в нашей таблице слишком мало чисел. Даже если для построения таблицы мы используем миллион простых чисел, таблица будет содержать всего лишь 37330 чисел. Это значит, что с помощью такой таблицы мы сможем отбраковать менее 4% чисел. Соответственно, и быстродействие программы мы повысим менее, чем на 4 %. Так что в данном случае усложнение программы не оправдано, потому что для большинства чисел (более 96%) будет применяться критерий Люка-Лемера.

Но оказывается, эффективные критерии простоты существуют не только для чисел Мерсенна! Эффективные критерии существуют, например, и для чисел вида k-2ⁿ +1.

Простые числа вида k*2ⁿ +1

Для чисел вида k*2ⁿ+1 существует весьма эффективный критерий простоты. Он состоит в проверке сравнения а2^n-1 =-1 (mod k*2ⁿ +1) для некоторого а. Однако выбор этого а зависит от k. Оказывается, нужно различать случаи, когда k не делится на 3 и делится на 3. Случай, когда k не делится на 3, совсем прост.

Случай, когда k не делится на 3

Если k не делится на 3, то, как заметил Прот (Proth) в 1878 году, числа k*2ⁿ +1 являются простыми при kⁿ+ 1 тогда и только тогда, когда 3^2n-1-1 (mod k-2ⁿ+l). Впрочем, эта традиционная формулировка критерия Прота несколько некорректна. В ней, например, (молчаливо!) исключается случай n = 1, k = 1. Для n =1, k - 1 имеем k = k3 = 2+1= 2" + 1, хотя З2""* =3sO (mod /n2ⁿ+1), причем *-2"+1 =3-простое число. Дело в том, что если число k-2ⁿ +1 простое, то в традиционной формулировке критерия Прота число3 должно быть квадратичным невычетом по модулю k-2ⁿ + l. Но при и= 1, k= 1 число k2ⁿ+l =3. Впрочем, n- 1, k- 1 — единственное решение уравнения k* 2ⁿ +1 =3 в целых числах, отличных от 0. (Уравнение k-2" + 1 =3 в целых числах имеет всего два решения: указанное только что решение n= 1, k= 1 и n = 0, k= 2.)

Разыскивая простые числа вида k*2ⁿ +1, конечно, нельзя ограничить перебор по и только простыми числами, но все равно многие значения отсеиваются тривиальным образом.

Пример 7.7. Простые числа вида 5-2ⁿ+ 1. Рассмотрим, например, случай k = 5. Тогда числа вида 5*2ⁿ +1 делятся на 3 при четных п. Так что перебор можем вести только по нечетным и.

Используя функцию PowerMod, очень легко запрограммировать критерий простоты.

Mk_nPrime[k_,n_]:=Module[{t = k*2An+l},

If[k<=2An+l,PowerMod[3,(t-1)/2,t]==t-l,PrimeQ[t]]]

А вот и программа для перебора по нечетным п.

Mkⁿ[k_,nl_]:=Block[{n=l},

While [n<=nl, {If[MknPrime[k,n],Print[п]], n+=2}]];

Теперь можем выполнить перебор. Mkn[5,300000]

Так можно получить (если хватит терпения) следующие значения я: 1, 3, 7, 13, 15, 25, 39, 55, 75, 85, 127, 1947, 3313, 4687, 5947, 13165, 23473, 26607, 125413, 209787, 240937.

Впрочем, при дневном счете терпение обычно улетучивается после печати числа 13165, если не раньше. Конечно, метод перебора можно усовершенствовать, заметив, что если остаток от деления и на 3 равен 2, то число 5*2ⁿ+1 делится на 7. Так что числа, дающие в остатке 2 при делении на 3, можно при переборе пропустить. Можно также пропустить числа, дающие в остатке 1 при делении на 10, поскольку тогда число 5*2ⁿ + 1 делится на 11. Можно, конечно, пойти и дальше. Можно, например, взять несколько небольших нечетных простых чисел д, для которых существует решение сравнения 5-2ⁿ+ 130 (mod q). Пусть s— показатели 2 по модулю q: 2s=1 (mod q). (Такое 5 можно найти с помощью функции MultiplicativeOrder [2, q].) Тогда при всех n^t (mod s) 5*2ⁿ + 1 = 0 (mod q). Если q не является числом вида 5*2ⁿ+1, все числа nst (mod s) можно опустить при переборе. Если же q является числом вида 5*2ⁿ +1, то нужно оставить только то число rmt (mod s), при котором 5*ⁿ + 1 = q. Эта идея вполне реализуема, но не слишком ли она усложняет перебор?

Давайте попробуем. Вот функция, которая по заданному номеру я простого числа q находит t — решение сравнения 5* 2ⁿ +1 = О (mod q) и i — показатель 2 по модулю q, если такое решение существует.

:[n]:=

51ock[{q= Prime[n],

s=MultiplicativeOrder[2,q],

t=MultiplicativeOrder[2,q,{-PowerMod[5,-I, q]} ] }, If[NumberQft],fs,t}]]

Теперь с помощью этой функции можно сгенерировать таблицу остатков и соответствующих им модулей.

Чтобы в таблице сначала шли меньшие модули 5 (они помогают отбраковать больше кандидатов), таблицу пришлось отсортировать, предварительно вычеркнув из нее элементы NULL, которые соответствуют тем простым модулям q, для которых сравнение 5*2ⁿ +1 = 0 (mod q) неразрешимо.

Каждая пара в этой таблице описывает арифметическую профессию из показателей, для которых выполняется некоторое тождественное сравнение. Пусть, например, в таблице имеется пара (s,. t). Она была получена для некоторого простого числа q.

Ее наличие в таблице означает, что 5*2ⁿ+1 + 1 = 0 (mod q) для любых натуральных k.

Теперь давайте не будем спешить с написанием программы, а предварительно оценим количество чисел, которые может помочь отбраковать такая таблица. Для этого сначала составим программу, которая подсчитывает количество чисел, отбракованных с помощью таблицы. Для этой программы нам понадобится функция, отбраковывающая заданное число по заданной таблице. Вот код этой функции.

fx[n_,t_]:=

Block!(1= Length[t],i=l,c=(i<=l)}, While[c,

{s,r}=t[[i]];answer=(Mod[n,s]!=r); i + +;

c=(i<=l)&&answer];answer]

Эта функция принимает значение True, если число n не было отсеяно с помощью таблицы t, т.е. если оно подлежит дальнейшему испытанию. Теперь можем составить программу подсчета отбракованных чисел.

prog:=

Block[fnn=200000,Yes=0,No=0, j=l}, While[j<=nn,

If[fx[j,t],Yes++,No++] ; J+-2]; Print ["Yes = ", Yes, "; No=",No] ]'

Конечно, количество отбракованных чисел и время отбраковки зависят от размера таблицы t. Сначала давайте возьмем совсем небольшую таблицу.

t=Sort[DeleteCases [Array [f, 10,4] ,Null].]

{{3,2},{10,1},{11,5},{12,9),(18,11),{20,3},{28,20},{36,31}}

Теперь запускаем программу.

prog//Timing Yes= 27274 ; N0= 72726

{5.188 Second,Null}

Как видите, за 5 секунд удалось отбраковать более 72 % чисел! Давайте попробуем увеличить таблицу.

t=Sort[DeleteCases[Array[f,25,4],Null]]

{{3,2}, {10,1}, {11,5},{12,9},{18,11},{20,3},{23,14},

{28,20},{36,31},{51 ,22},{52,31},{58,23},

{60,8},{66,18},{82,14},{100,26},{106,6}}

Опять считаем процент отбракованных чисел и замеряем время:

prog//Timing Yes= 23152 ; N0= 76848

{6.985 Second,Null}

Время отбраковки возросло менее, чем на 2 секунды, а отбраковали мы почти 77 % чисел! Значит, таблицу стоит увеличить.

t=Sort[DeleteCases[Array[L,100,4],Null]] ;

Опять измеряем время:

prog//Timing Yes = 18329 ;

No= 81671 (14.047 Second,Null}

Как видим, таблицу увеличивать стоило! Время отбраковки, конечно, возросло, притом более чем вдвое, но 14 секунд по сравнению с часами счета роли не играют. Так что увеличение таблицы окупает себя! Увеличиваем таблицу еще.

t=Sort[DeleteCases[Array[f,1000,4],Null]];

Теперь снова измеряем время и процент отбраковки:

prog//Timing Yes=12827;
N0= 87173 {74.172 Second,Null}

Конечно, время возросло: теперь отбраковка занимает более одной минуты. Но проверять по-настоящему придется менее 13 % чисел! Потратив дополнительно на предварительную отбраковку чуть более минуты, мы почти в 8 раз уменьшим количество чисел, которые надо будет проверить на простоту. Оказывается, увеличение таблицы оправдало себя и на этот раз. Поэтому еще раз увеличиваем таблицу.

t=Sort[DeleteCases[Array[f,10000,4],Null]];//Timing

{89.969 Second,Null}

На этот раз сама генерация таблицы занимает более минуты. Но и это время окупается.

prog//Timing Yes= 9821 ; N0= 90179

{527.781 Second,Null)

Количество чисел, которые подлежат проверке на простоту, мы уменьшили более чем в 10 раз! Может быть, стоит увеличить таблицу еще? Ну, на этот раз, во всяком случае, уж точно не в 10 раз. Ведь ждать генерации таблицы несколько часов — занятие весьма неприятное! Поэтому лучше сначала попытаться увеличить таблицу, скажем, в 2,5 раза.

t=Sort[DeleteCases[Array[f,25000,4],Null]]///Timing

{638.234 Second,Null}

На генерацию таблицы понадобилось более десяти с половиной минут. Заметно, что время генерации таблицы растет нелинейно с ростом таблицы. Наверное, пора остановиться. Проверяем:

prog//Timing Yes= 8985 ; N0= 91015

{1201.44 Second,Null}

На отбраковку потрачено более двадцати минут. Это на 9,39063 минут больше, чем в предыдущем случае. Несмотря на все это, дополнительно отбраковать удалось менее одного процента чисел. Действительно, пора остановиться. (Надо признать, конечно, что это довольно грубый, притом субъективный критерий останова.)

Теперь можем приступить к написанию программы. Пусть ее заголовок (имя и список параметров) будет М5п[п_]. (Параметр n — верхний конец диапазона, в котором происходит перебор.) Прежде всего нужно решить следующий вопрос: как использовать таблицу так, чтобы не пропустить ни одного простого числа вида 5-2ⁿ+1 даже в том случае, если оно использовалось при построении таблицы. Конечно, можно заблаговременно составить список n для таких чисел. Но это значит, что список п для таких чисел нужно составить по другой программе, решающей фактически ту же задачу, решением которой мы сейчас как раз и заняты. При решении этой вспомогательной задачи, правда, можно ограничиться перебором на меньших начальных отрезках натурального ряда. Конечно, этот способ решения вполне корректен. Но такой способ ведет к программе, которая выглядит несколько искусственно. Фактически получится не программа, а подглядывание в раздел ответов в случае небольших значений п. Ничего плохого в этом нет. Просто этот способ реализовать нельзя, если мы не знаем нужную нам часть ответа для решаемой задачи. Поэтому поступим иначе. Мы вообще сделаем вид, что не знаем даже начальных значений п. Сначала в программе найдем все те начальные значения n, при которых числа вида 5*2ⁿ+1не превосходят тех простых чисел q, которые использовались для построения таблицы. Хотя это и будет чистый перебор, перебирать придется недолго, поскольку числа вида 5*2ⁿ +1 с ростом и растут гораздо быстрее, чем и-е простое число рn. Например, если мы будем строить таблицу, используя первые 25 000 простых чисел, то перебирать без дополнительной отбраковки придется лишь первый десяток нечетных значений п. Затем можно будет построить таблицу и запустить процесс предварительной отбраковки. Поскольку проверка малых значений выполняется весьма быстро, о времени ее выполнения можно не беспокоиться. Может возникнуть и противоположный вопрос» не слишком ли рано мы запускаем отбраковку? Но мы видели, что даже отбраковка 100 000 нечетных чисел с помощью огромной таблицы, построенной с использованием первых 25 000 простых чисел, занимает всего лишь чуть более 20 минут. Так что на предварительную отбраковку одного числа требуется совсем немного времени. Ну а выигрыш отбраковка дает уже при весьма малых значениях и. Поэтому не стоит беспокоиться из-за того, что на некотором, весьма малом отрезке отбраковка может оказаться менее эффективной, чем прямая проверка. Для таблицы, построенной с использованием первых 25 000 простых чисел, перерасход времени, например, не превысит 12 секунд. Так что беспокойство по поводу того, что временные затраты на отбраковку малых значений и могут быть больше, чем на прямую проверку, необоснованно. Но перед запуском отбраковки нужно сгенерировать таблицу t. Даже если таблица строится с использованием первых 10 000 простых чисел, генерация таблицы занимает более минуты. Хотя это время (и даже большее) окупается, поведение программы из-за временных затрат на построение таблицы может показаться несколько неожиданным. Действительно, сначала очень быстро печатаются первые значения п, затем происходит весьма заметная (но необъяснимая, если не знать причину) задержка из-за генерации таблицы, после чего опять довольно быстро печатается следующая серия небольших значений и и лишь затем (на моем компьютере после и = 5947) опять происходит весьма существенная задержка. Она связана как с отсутствием искомых значений я вплоть до n= 13165, так и с тем, что для части чисел (менее 10 %) приходится выполнять полную проверку, которая теперь уже требует весьма ощутимых временных затрат. В приведенной ниже программе учтено все, о чем говорилось выше.

М5n[n_]:=

Block[{j=l,nnprime=25000,primen=Prime[nnprime],nn=Min[n,primen]},

While [5*2Aj+l<=primen&& j<=n,{If[MknPrime[5,j],Print[j]],j+=2}];

If[j<n,

t=Sort[DeleteCases[Array[f,nnprime,4],Null]];While!j<=nn,

If[fx[j,t],If[MknPrime[5,j],Print[j]]]; j+=2]]]

Эта программа существенно быстрее первоначальной, и даже за короткую летнюю ночь она сможет на весьма слабеньком ПК (по нынешним представлениям, конечно) найти n = 26607.

Ну и, наконец, мораль этой истории. Хотя поначалу казалось, что предварительная отбраковка сильно усложнит программу, оказалось, что в системе Mathematica есть все необходимые функции для того, чтобы компактно записать построение необходимой таблицы и тем самым ускорить выполнение программы более чем в 10 раз!

Случай k = 3

Критерий простоты чисел вида 3*2ⁿ + 1 несколько сложнее. Впрочем, вся сложность заключается в выборе основания а, для которого проверяется сравнение аm =-1(mod k2ⁿ +1). Если и не делится на 4, то в качестве а достаточно взять 5. Иными словами, если п не делится на 4, то 3*2ⁿ+ 1 будет простым тогда и только тогда, когда 52"~'* з-1 (mod £-2"+1).

Вот как можно реализовать этот способ. Сначала определим вспомогательную функцию:

MMkn[k_, n_]: = k*2An+l

Теперь запишем критерий простоты.

MMSnPrimeOl[n_]:= Module[{t=3*2^n+1},

If[Mod[n,4]!=0,PowerMod[5,(t-1)/2,t]==t-l,PrimeQ[t]]]

После этого можем написать программу поиска тех и, при которых число 3*2ⁿ +1 является простым.

ММ3n[n_]:=

Block[{i=l}, While [i<=n, {If[MM3nPrime01[i],Print[i]], i++}]];

Конечно, данная программа работает существенно быстрее, чем написанная нами ранее для той же цели. Но все же давайте попробуем применить предварительный отсев.

Конечно, метод перебора можно усовершенствовать, если найти арифметическую прогрессию таких показателей п, для которых число 3*2ⁿ+1 делится на некоторое простое число д. Тогда показатели n, являющиеся членами этой прогрессии, при переборе можно пропустить, если 3*2ⁿ+1< q. Иными словами, можно пропустить те показатели п из этой прогрессии, для которых число 3*2ⁿ+1>q. Можно, конечно, пойти и дальше. Можно, например, взять несколько небольших нечетных простых чисел <?, для которых существует решение сравнения 3*2ⁿ+1^0 (mod q). Пусть s — показатель 2 по модулю q: T=\1(mod q). (Такое s можно найти с помощью функции MultiplicativeOrder [2, q].) Тогда при всех tmt (mod s) число 3-2ⁿ +1 = 0 (mod q). Если q не является числом вида 3*2ⁿ+1 , все числа и=/ (mod s) можно опустить при переборе. Если же q является числом вида 3*2ⁿ +1, то нужно оставить только то число n=t (mod 5), при котором 3-2ⁿ+1 — q. Иными словами, мы сможем отбраковать все те показатели п, которые принадлежат хотя бы одной из построенных нами указанным выше способом арифметических прогрессий. Как мы видели на примере чисел вида 5-2ⁿ+1, эта идея значительно повышает быстродействие программы и практически не усложняет перебор. Однако в данном случае таблицы получатся, конечно, совсем другие, и потому оптимальные параметры (главный из них — размер таблицы) придется подбирать заново.

Сначала определим функцию, которая по заданному номеру п простого числа q находит t — решение сравнения 3*2ⁿ+1^0 (mod q) и 5 — показатель 2 по модулю q, если такое решение существует.

f3[n_]:=

Block!(q=  Prime[n],

s=MultiplicativeOrder[2,q],

 t=MultiplicativeOrder[2,q,{-PowerMod[3, -l,q]}]},

If[NumberQ[t],fs,t}]]

Теперь с помощью этой функции можно сгенерировать таблицу остатков и соответствующих им модулей.

Чтобы в таблице сначала шли меньшие модули s (они помогают отбраковать больше кандидатов), таблицу пришлось отсортировать, предварительно вычеркнув из нее элементы NULL, которые соответствуют тем простым модулям д, для которых сравнение 3*2ⁿ +1 = 0 (mod q) неразрешимо.

Каждая пара в этой таблице описывает арифметическую профессию из показателей, для которых выполняется некоторое тождественное сравнение. Пусть, например, в таблице имеется пара (s, t). Она была получена для некоторого простого числа q. Ее наличие в таблице означает, что 3*2ⁿ⁺¹+1 = 0 (mod q) для любых натуральных k.

Теперь давайте предварительно оценим количество чисел, которые может помочь отбраковать такая таблица. Для этого сначала составим программу, которая подсчитывает количество чисел, отбракованных с помощью таблицы. Для этой программы нам понадобится функция, отбраковывающая заданное число по заданной таблице. Вот код этой функции.

fx[n_,t_]:=

Block[{1= Length[t],i=l,c=(i<=l) }, While[c,

{s,r}=t[[i]]; answer= (Mod [M, s] !=r) ; i++;

c=(i<=l)S&answer]; answer]

Эта функция принимает значение True, если число я не было отсеяно с помощью таблицы t, т.е. если оно подлежит дальнейшему испытанию. Теперь можем составить программу подсчета отбракованных чисел.

prog:=

Block[{nn=l00000,Yes=0,No=0,j=l}, While[j]=nn,

If[fx[j,t],Yes++,No++]; J++1;

 Print["Yes=",Yes,"; No=",No]]

Заметьте, что программа отличается от аналогичной программы для чисел вида 5*2ⁿ+ 1. Отличие связано с тем, что на этот раз перебор не ограничивается только нечетными показателями. Конечно, как и для чисел вида 5-2ⁿ + 1, количество отбракованных чисел и время отбраковки зависят от размера таблицы t. Сначала давайте сгенерируем совсем небольшую таблицу.

t=Sort[DeleteCases[Array[f3,10,3] ,Null]]

{{3,1},{4,3},{10,7},{12,2],{18,14],{28,9),{36,28}}

Теперь запускаем программу.

prog//Timing Yes= 33650 ; N0= 66350

{4.937 Second,Null}

Как видите, менее чем за 5 секунд удалось отбраковать более 66 % чисел! Давайте попробуем увеличить таблицу.

t=Sort[DeleteCases[Array[f3,25,3],Null]]

{{3,1},{4,3},{10,7),{12,2},{18,14),{28,9},{36,28),{39,29},

{48,5},{51,4 2},{52,9},{58,37},{60,24},{66,60},{82,51},{100,81}}

Опять считаем процент отбракованных чисел и замеряем время.

prog//Timing Yes= 25645 ; N0= 74355

{7.188 Second,Null}

Время отбраковки возросло чуть более чем на 2 секунды, а отбраковали мы более 74 % чисел! Значит, таблицу стоит увеличить.

t=Sort[DeleteCases[Array[f3,100,3], Null]];

Опять измеряем время.

prog//Timing Yes = 21055 ; N0= 78945

{14.765 Second,Null}

Как видим, таблицу увеличивать стоило! Время отбраковки, конечно, возросло, притом более чем вдвое, но 15 секунд по сравнению с часами счета роли не играют. Так что увеличение таблицы окупает себя! Увеличиваем таблицу еще.

t=Sort[DeleteCases[Array[f3,1000,3],Null]];

Теперь снова измеряем время и процент отбраковки.

prog//Timing Yes= 15388 ; N0= 84612

{84.64 Second,Null}

Конечно, время возросло: теперь отбраковка занимает более одной минуты. Но проверять по-настоящему придется чуть более 15 % чисел! Потратив дополнительно на предварительную отбраковку немногим более одной минуты, мы почти в 8 раз уменьшим количество чисел, которые надо будет проверить на простоту. Так что увеличение таблицы оправдало себя и на этот раз. Поэтому еще раз увеличиваем таблицу.

t=Sort[DeleteCasestArray[f3,l0000,3],Null]];//Timing

{90.703 Second,Null}

На этот раз сама генерация таблицы занимает более полутора минут. Но и это время окупается.

prog//Timing Yes = 12123 ; N0= 87877

{630.734 Second,Null}

Количество чисел, которые подлежат проверке на простоту, мы уменьшили более чем в 8 раз! Может быть, стоит увеличить таблицу еще? Ну, на этот раз, во всяком случае, уж точно не в 10 раз. Ведь ждать генерации таблицы несколько часов — занятие весьма неприятное! Поэтому лучше сначала попытаться увеличить таблицу, скажем, в 2,5 раза.

t=Sort[DeleteCases[Array!f3,25000,3],Null]];//Timing

{629.781 Second,Null}

На генерацию таблицы понадобилось почти десять с половиной минут. Заметно, что время генерации таблицы растет нелинейно с ростом таблицы. Наверное, нужно проверить, не пора ли остановиться.

prog//Timing Yes= 11129 ; N0= 88871

{1405.2 Second,Null}

На отбраковку потрачено почти двадцать четыре минуты. Это существенно больше, чем в предыдущем случае. Несмотря на это, дополнительно отбраковать удалось чуть более одного процента чисел. Кажется, пора остановиться. (Конечно, это довольно грубый и притом субъективный критерий останова.)

Теперь можем приступить к написанию программы. Пусть ее заголовок (имя и список параметров) будет М3n[n_]. (Параметр n— верхний конец диапазона, в котором происходит перебор.) Прежде всего нужно решить следующий вопрос: как использовать таблицу так, чтобы не пропустить ни одного простого числа вида 3*2ⁿ+1 даже в том случае, если оно использовалось при построении таблицы. Конечно, можно заблаговременно составить список n для таких чисел. Но это значит, что список п для таких чисел нужно составить по другой программе, решающей фактически ту же задачу, «решением которой мы сейчас как раз и заняты. При решении этой вспомогательной задачи, правда, можно ограничиться перебором на меньших начальных отрезках натурального ряда. Конечно, этот способ решения вполне корректен. Но он ведет к программе, которая выглядит несколько искусственно. Фактически получится не программа, а подглядывание в раздел ответов в случае небольших значений п. Ничего плохого в этом нет. Просто этот способ реализовать нельзя, если мы не знаем нужную нам часть ответа для решаемой задачи. Поэтому мы поступим иначе. Мы вообще сделаем вид, что не знаем даже начальных значений п. Сначала найдем в программе все те начальные значения n, при которых числа вида 3*2ⁿ+1 не превосходят тех простых чисел q, которые использовались для построения таблицы. Хотя это и будет чистый перебор, перебирать придется недолго, поскольку числа вида 3*2ⁿ +1 с ростом и растут гораздо быстрее, чем n-е простое число р^а. Например, если мы будем строить таблицу, используя первые 25 000 простых чисел, то перебирать без дополнительной отбраковки придется лишь три-четыре десятка значений п. Затем можно будет построить таблицу и запустить процесс предварительной отбраковки. Поскольку проверка малых значений выполняется весьма быстро, о времени ее выполнения можно не беспокоиться. Конечно, вполне законным является и вопрос: не слишком ли рано мы запускаем отбраковку? Но мы видели, что даже отбраковка 100 000 чисел с помощью огромной таблицы, построенной с использованием первых 25 000 простых чисел, занимает не более 24 минут. Так что на предварительную отбраковку одного числа требуется совсем немного времени. Ну а выигрыш отбраковка дает уже при весьма малых значениях п. Поэтому не стоит беспокоиться из-за того, что на некотором, весьма малом отрезке отбраковка может оказаться менее эффективной, чем прямая проверка. Для таблицы, построенной с использованием первых 25 000 простых чисел, перерасход времени, например, не превысит десятка-двух секунд. Так что беспокойство по поводу того, что временные затраты на отбраковку малых значений n могут быть больше, чем на прямую проверку, необоснованно. Но перед запуском отбраковки нужно сгенерировать таблицу t. Даже если таблица строится с использованием первых 10 000 простых чисел, генерация таблицы занимает немного более полторы минуты. Кроме того, в данной программе есть еще один источник непредсказуемых временных затрат. Это показатели n, кратные 4. Давайте сначала посмотрим, что это будут за показатели. Вот нужная нам программа.

prog401 : =

Block[{nn=8000,Yes=0,No=0,j=4), While[j<=nn,

If[fx[j,t],Print[j,","];Yes++,No++]; j +=4];

Print["Yes=",Yes,";   No=",No]]

В пределах первых восьми тысяч будет найдено 401 число, кратное 4, такое, что его не удастся отсеять с помощью таблицы, для генерации которой использовались 25 000 простых чисел. (Отсеяно будет 1599 чисел.) Далее приведен список тех чисел, которые кратны 4 и выдерживают отсев.

Если показатель я равен одному из этих чисел, то наименьший делитель числа 3*2ⁿ+ 1, больший единицы, больше наибольшего простого модуля, использованного для составления таблицы. Вот примеры.

Factor-Integer [3*2АЗб+1]

{(206158430209,1}} Factorlnteger[3*2Л92+1]

{{1132314641089,1},{13119392730926401,1}} Factorlnteger[3*2л96+1]

{{392840481939253,1},{605040718740253,1}} Factorlnteger [3*2лЮ8+1]

{{805213,1},{1781311693519,1},{678750386188027,1}}

Таким образом, нетривиальные делители чисел 3*2ⁿ +1, показатели которых выдержали отсев, довольно велики. (Ведь если число 3*2ⁿ +1 делится на простой модуль, использованный при построении таблицы, то показатель не выдержал отсев.) Поэтому при применении функции PrimeQ могут произойти временные задержки. Давайте сосчитаем количество таких показателей в пределах первых 300 000. Вот нужная нам программа.

prog4:=

Block[{nn=30000,Yes=0,No=0, j=4}, While[j<=nn,

If[fx[j,t],Yes++,No++]; j+=4];

Print["Yes=",Yes,"; No=",No]]

Вот результаты счета.

prog4//Timing Yes= 14451 ; N0= 60549

{1893.61 Second,Null}

Как видите, в пределах первых 300000 придется проверить только 14451 число, кратное 4. Правда, отсев остальных чисел при этом у меня занял примерно 1893 секунды, т.е. чуть больше получаса.

Хотя, как и в случае чисел 5*2ⁿ +1, время на построение таблицы окупается, поведение программы может показаться несколько неожиданным из-за временных затрат на построение таблицы и возможных временных затрат на вычисление функции PrimeQ в случае показателей, кратных 4. Действительно, сначала очень быстро печатаются первые значения п, а затем после n = 534 (на моем компьютере) происходит весьма существенная задержка. Она связана как с отсутствием искомых значений и вплоть до п = 2 208, так и с тем, что для части чисел (чуть более 11 %) приходится выполнять полную проверку, которая теперь уже требует весьма ощутимых временных затрат, причем зачастую весьма непредсказуемых для показателей п, кратных 4. Затем выдача замедляется, но поведение программы выглядит вполне стабильно, пока не будет напечатан показатель n = 3 912. После этого идет большой перерыв, вплоть до w = 20 909. В приведенной ниже программе учтено все, о чем говорилось выше.

М3n[n_]:=

Block[{j=l,   nnprime=25000,primen=Prime[nnprime],nn=Min[n,primen]},

While   [MMkn[3,j]<= primen   &&   j<=n,

{If[MM3nPrime01[j],Print[j]], J++H; If[j]<n,

t=Sort[DeleteCases[Array[f3,nnprime, 3] , Null]] ;

 While[j]=nn,

If[fx[j,t],

  If[MM3nPrime01[j],Print[j]]] ; j++]]]

Эта программа существенно быстрее первоначальной, но если хотите по ней найти n = 20 909, понадобится время и ангельское терпение.

Как видим, предварительная отбраковка и в данном случае значительно повышает эффективность программы. Впрочем, эффективность программы все еще сильно определяется неотсеянными показателями n, кратными 4. Хотелось бы и для них найти такое основание а, чтобы для установления простоты числа 3*2ⁿ+1 достаточно было проверить выполнение сравнения ат k =-1 (mod /a2ⁿ+l). (Ранее для показателей n, не кратных 4, мы полагали а = 5.)

Но все дело в том, что если показатель п делится на 4, то выбрать основание а несколько сложнее. Если показатель п делится на 4, в качестве основания а можно взять любой квадратичный невычет г по модулю 3 * 2ⁿ +1. Поэтому если п делится на 4, то сначала нужно найти (желательно небольшой) квадратичный невычет t по модулю 3*2ⁿ+1, а затем проверить, выполняется ли сравнение n2^n-1=-1(mod k*2ⁿ+l). Но как найти квадратичный вычет? Для этого можно использовать квадратичный закон взаимности.

Если Р>1 n Q>1 — положительные нечетные взаимно простые числа, то

Прежде всего заметим, что если Р — 3*2ⁿ +1, то

Поэтому

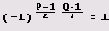
Как видим, для поиска квадратичного невычета r можно использовать функцию JacobiSymbol. В качестве г можно брать небольшие нечетные числа и вычислять для них символ Якоби. (Для квадратичного невычета символ Якоби равен -1.) Как только мы найдем квадратичный невычет r, можем проверить, выполняется ли сравнение r_{2 k} =-1 (mod 32ⁿ+l). Теперь легко написать функцию, вычисляющую квадратичный невычет.

ММ3nr[nn_]:= Module[{r=5,

JS=JacobiSymbol[5, nn]}, While[JS!=-1   &&   r<nn, r+=2; If[GCD[r,nn]= =1,

JS=JacobiSymbol[r,nn]]];r]

Чтобы запрограммировать критерий простоты, воспользуемся функцией PowerMod.

MMSnPrime[n_]:= Module[{t =  3*2^n+1), If[Mod[n,4]!=0,

PowerMod[5,(t-1)/2,t]==t-l,

PowerMod[ММЗnr[t],(t-1)/2,t]==t-l]]

Теперь, наконец, можем написать окончательную версию программы.

M3nv01[n_]:=

Block[{j=l» nnprime=25000,primen=Prime[nnprime],

nn=Min[n,primen]},

While   [MMkn[3,j]<= primen && j<=n,

 {If[MM3nPrime[j],Print[j]], J++H; If[j<n,

t=Sort[DeleteCases[Array[f3,nnprime,3],Null]]; While[j<=nn,

If[fx[j,t], If[MM3nPrime[j],Print[j]]];j++]]]

Запуская программу с параметром nnprime = 10000 и 25000, убеждаемся, что при этих (и всех промежуточных) значениях генерация таблицы начинается после вывода показателя 12, но до вывода показателя 18. Затем программа довольно быстро добирается до показателя 3912, после вывода которого "уходит в себя" аж до вывода показателя 20 909. (Заметьте, что, в отличие от предыдущей версии программы, перерыв между показателями 534 и 2 208 не слишком заметен — эту "достопримечательность" вы запросто можете пропустить, если выйдете выпить чашечку кофе!)

Оказывается, что число 3*2ⁿ+ 1 является простым при n = 1, 2, 5, 6, 8, 12,

18, 30, 36, 41, 66, 189, 201, 209, 276, 353, 408, 438, 534, 2 208, 2 816, 3 168, 3 189, 3 912, 20 909, 34 350,. 42 294, 42 665, 44 685, 48 150, 55 182, 59 973, 80 190, 157 169, 213 321. При всех других n, не превосходящих 300 000, число 3*2ⁿ + 1 яляется составным.

и основу основ модулярной арифметики

Мы рассмотрели определение частного (функция Quotient) и остатка (функция Mod), а также возведение в степень в модулярной арифметике (функция PowerMod) и основу основ модулярной арифметики — китайскую теорему об остатках (функция ChineseRemainder). Кроме того; мы затронули вопрос об извлечении квадратных корней (функции SqrtMod, SqrtModList и JacobiSymbol). Но мы не ограничились корнями второй степени, а научились находить первообразные корни по модулю n (функция PrimitiveRoot), а также показатели (функция MultiplicativeOrder). Как оказалось, некоторые из рассмотренных функций используют каноническое разложение (функцию Factorlnteger) и потому не могут справиться с вычислениями при очень больших аргументах. Однако на реальных примерах мы убедились в том, что эти функции очень полезны и вполне пригодны даже тогда, когда вычисления ведутся с очень большими числами, например с числами, близкими к тысячным, десятитысячным, стотысячным и даже миллионным степеням двойки.