Алгебра и пакет Mathematica 5
Функция Эйлера — EulerPhi
Если в полной системе вычетов по модулю nоставить только вычеты, взаимно простые с модулем, получим приведенную систему вычетов по модулю n. Мощность приведенной системы вычетов по модулю
n как множества обозначается φ(n), а функция
φ:n->φ(n) называется функцией Эйлера. Найдем, для примера, приведенную систему вычетов по модулю 10.
Select[Range[10],GCD[fl,10]==!&]
{1,3,7,9}
Приведенная система вычетов по модулю 10, как видим, содержит 4 элемента. Значит,φ(10) = 4. В системе Mathematica функция Эйлера имеет имя EulerPhi. Вот как можно вычислить φ(10).
EulerPhi[10]
4
Функция Эйлера имеет замечательные свойства и многочисленные применения. Например, она обладает следующим свойством:
Если а и т взаимно простые, то аφ(m) = 1(modm).
Это утверждение называется теоремой Эйлера и очень часто малой теоремой Ферма, который знал ее частный случай для простых модулей т. Эта теорема позволяет упростить вычисление остатков степеней чисел, взаимно простых с модулем. Рассмотрим пример.
Пример 8.1. "Бытие Бога". Во второй половине XIX века некоторых авторов привлекали числа 22, З3 , 44 . Вот что пишет об этих числах известный немецкий популяризатор математики Вальтер Литцман в середине XX столетия:
В одной, изданной в 1874 году книге под названием "Бытие Бога" (автор книги — Крениг) рассматривается ряд чисел: 22, З3 , 44 .О последнем из этих чисел автор говорит: "Представьте себе отрезок такой длины, что световому лучу понадобился бы квинтиллион лет, чтобы пройти этот путь. Затем представьте себе шар с диаметром, равным этому отрезку, наполненный типографской краской. Всей этой краски не хватило бы, чтобы четко напечатать это число даже самыми мелкими цифрами, какие только существуют". X. Маурер исследовал эти числа с точки зрения теории чисел. Обозначив для простоты число Xх через 3x: и введя затем общее обозначение nх = хm (где хил — целые положительные числа), он показал, как можно найти последние цифры этих числовых великанов. Так, например, 29 (т. е. 99) оканчивается на 89, 39 — на 289, 49 — на 5289, 59 — на 45 289 и так далее, наконец, 109 — на 9 392 745 289. Таким образом, последние n цифр числа "9 повторяются во всех последующих числах "+19, "+29 , ... и т.д. Аналогичными свойствами обладает и любой другой ряд 1х = х, 2х , 3х, ... и так далее, где х — целое.
Что вы чувствуете по мере чтения этого отрывка? Я чувствую интерес и нарастающее недоверие. Я, например, в захвате от сравнения с шаром. Но я сомневаюсь, заканчивается ли 109— на 9 392 745 289. И даже если последние и цифр числа "9 повторяются во всех последующих числах "+19, "+29, ... и так далее, то я полагаю, что это как-то связано с девяткой и с тем, что эти числа записываются в десятичной системе счисления. Едва ли такими свойствами обладает и любой другой ряд 1х = х, 2х , x , ... и так далее, где х — целое. И действительно, i2 = 2 заканчивается на 2, а 2 х = 4 — на 4. Уже последняя цифра не повторяется во всех последующих числах этого вида! Как можно говорить о повторении последних n цифр числа? Так что насчет таких свойств у любого другого ряда 1х = х, 2х , 3x... и так далее, где х — целое, то тут явное вранье. Вальтер Литцман, правда, говорит не о таких свойствах, а об аналогичных свойствах, но в чем отличие, не указывает явно. Такими свойствами не обладают, например, числа х = 3, 4, 8 и многие другие. Поэтому в чем именно состоит аналогия, для меня пока не совсем понятно. И мне, естественно, хочется прояснить этот вопрос и еще сильнее хочется вычислить последние и цифр числа n9.
Давайте начнем с вычисления последних n цифр числа n9. Как это сделать с помощью системы Mathematica?
Вот определение функции nх .
GodF[n_,x_]:=Module[{t=1},Do[t=xAt,[i,n}];t]
Функция "х возрастает очень быстро, значительно быстрее факториалов, поэтому, если нужно вычислить, скажем, последние k знаков какого-нибудь значения этой функции, необходимо использовать PowerMod.
GodFLastk[n_,x_,k_] :=
If [n==l,Mod[x,10Ak],PowerMod[x,GodF[n-l, х],IQ^k] ]
Пусть k = 50. Тогда мы в мгновение ока сможем вычислить последние 50 знаков чисел 19, 29 и 39. Но вот вычислить последние даже 10 знаков числа 49 так легко не удастся. Этот пример показывает, что в некоторых случаях применение функции PowerMod может продвинуть вычисления всего лишь на один шаг!
Но функция Эйлера (и малая теорема Ферма) позволяет быстро вычислить последние 50 знаков числа "9. Программа, конечно, будет другая.
PowerMod[9,PowerMod[9,9A9,EulerPhi[10^50]],1^50]
30363975097419408973491530163140828233401045865289
Можно ли быстро вычислить последние 50 знаков числа 59 по такой программе?
PowerMod[9,PowerMod[9,9Л9Л9,EulerPhi[10Л50]],10^50]
Едва ли.
В чем же причина такого медленного продвижения, почему мы продвигаемся только на один шаг? Это происходит потому, что мы на самом деле устраняем быстрый рост функции nx = x(nf} только на последнем шаге. Почему это происходит? Потому, что мы все время связаны с определением функции GodF. Именно она используется внутри функции GodFLastk. Даже фактически отказавшись от явного применения функции GodFLastk, мы все равно стремимся записать выражение для nх = х(nn) с некоторыми упрощениями для последнего или предпоследнего возведения
в степень. Конечно, это так естественно использовать выражение для "х = х(') Однако нужно иметь в виду, что использование подобных "прямолинейных" определений часто весьма неэффективно. Если уж мы решили повышать эффективность, то делать это нужно на всю "глубину" выражения. Правда, это неизбежно приведет к появлению новых функций. Нам, например, придется отказаться от функции GodFLastk. Как ни удивительно, но вместо нее нам понадобится только одна функция, притом довольно простая. Давайте найдем ее определение. Обозначим через С(n, х, k) остаток от деления "х на k. (Таким образом, G(n, х, m) — это последние т цифр числа nх .) Тогда 0(1, х, k) = Mod [х, k]. С другой стороны,
С(n+1,x,k)=Mod[ хn,k]=PowerMod[x,"x ,k].
Предположим теперь, что х и k взаимно просты. Тогда по малой теореме Ферма это выражение можно записать так: PowerMod [x, G(n, х, ср(А:)), k]. Так что в этом случае G(n+l, x, k) = PowerMod [x, G(n, x, <p(k)), k]. Это и есть нужное нам рекуррентное соотношение. С учетом этого соотношения определение нужной нам функции выглядит так.
GodFk[n_,x_,k_]:=
If[n==l,Mod[x,k],
If[GCD[x,k]==l,PowerMod[x,GodFk[n-l,x, EulerPhi[k]],k],
PowerMod[x,GodF[n-l,x] , k]]];
Теперь легко написать программу.
Do[Print["n=",n,":",GodFk[n,x=9,10/sk]],{n,k=50}]
Давайте теперь выполним аналогичные вычисления для числа 3. Вот так запишется программа.
Do[Print["n=",n,":",GodFk[n,x=3,10Ak]],{n,k=50}]
Теперь понятно, что имел в виду Вальтер Литцман под аналогичными свойствами. Начиная с некоторого и = и„ последняя цифра числа не изменяется, причем начиная
с и = «() + 1 повторяются уже две цифры, с n = n0+2 — три цифры, с n = n0+k — k цифр и т. д. (Через и„ (х) удобно обозначать наименьшее п0 с таким свойством.) Для некоторых х, например для х = 9, n(х) = 1, а для некоторых х (n)>1. Если п0(х)>1, то нельзя утверждать, что последние n цифр числа "х повторяются во всех последующих числах "+1x, "+2х, ... и т.д. Если п0(х)>1, то повторение последних nцифр начнется не с числа "х, а несколько позднее! Да уж, разбираться в популярных книжках иногда приходится с системой Mathematical
Пример 8.2. График функции Эйлера.
Давайте теперь построим график функции Эйлера. Сначала используем функции Table и EulerPhi для построения таблицы tl (точнее, списка) значений функции Эйлера.
t1= Table[EulerPhi[k],{k,1,n=10A3}];
Теперь можем использовать функцию ListPlot для построения графика.
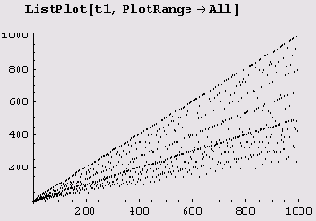
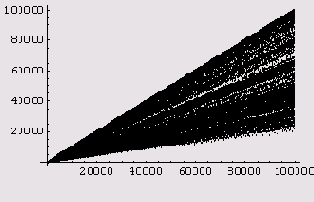
А вот график для n = 100000.
Функция Кармайкла λ(m) — CarmichaelLambda
Если а и т взаимно простые, то a4n-10 =}(modm). Но всегда ли φ(m) является наименьшим натуральным числом с таким свойством? Оказывается, нет. Например, для модуля 8 имеем следующую приведенную систему вычетов.
s=Select[Range[8],GCD[#,8]==!&]
{1,3,5,7}
Квадраты этих вычетов сравнимы с 1 по модулю 8.
Mod[%-2,8]
{1,1,1,1} Однако
EulerPhi[8]
4
Так что φ(8) не является наименьшим натуральным числом, удовлетворяющим сравнению an =l(mod8) для всех а, взаимно простых с 8.
Значения, меньшие φ(n), иногда доставляет обобщенная функция Эйлера ). Вдвое меньшие значения для модулей, кратных 8, дает функция Люка φ(x). А наименьшее натуральное число, удовлетворяющее сравнению аi =1 (mod от) для всех а,
взаимно простых с т, обозначается N/n). Функция А. называется функцией Кармайкла. В системе Mathematica у нее имя CarmichaelLambda.
Вот как можно вывести те натуральные числа, для которых k(m)<<р(m).
Do[If[EulerPhi[n]!=CarmichaelLambda[n],
Print[n,":",EulerPhi[n],":",CarmichaelLambda[n]]],{n,k=100}]Выполните эту программу, и вы увидите, что их довольно много.
Пример 8.3. График функции Кармайкла.
Давайте теперь построим график функции Кармайкла. Сначала мы используем функции Table и CarmichaelLambda для построения таблицы tl (точнее, списка) значений функции Кармайкла.
tl= Table[CarmichaelLambda[k],
{k,1,n=10A3)]; Теперь можем использовать функцию ListPlot для построения графика.

А вот график для n = 100000.

Сравните эти графики с графиками функции Эйлера. Сразу видно, что лучи на графике функции Кармайкла прижимаются к оси абсцисс гораздо ближе, чем на графике функции Эйлера.
Функция Мебиуса µ(m) — MoebiusMu
Функция Мебиуса µ(m) = 1, если т есть произведение четного числа различных простых чисел; µ(m) = -1, если m есть произведение нечетного числа различных простых чисел; (f(/n) = 0, если т делится на квадрат какого-либо простого числа. Вот как вычисляется эта функция.
MoebiusMu[210]
1
Пример 8.4. График функции Мебиуса.
Давайте теперь построим график функции Мебиуса. Сначала мы используем функции Table и MoebiusMu для построения таблицы tl (точнее, списка) значений функции Мебиуса.
tl= Table[MoebiusMu[k],
{k,1,п=10^3}]; Теперь можем использовать функцию ListPlot для построения графика.

Функции, связанные с делителями, — Divisors и DivisorSigma
Делители натурального числа легко найти с помощью системы Mathematica. Для этого предусмотрена функция Divisors. Найдем, например, делители 120.
Divisors[120]
{1,2,3,4,5,6,8,10,12,15,20,24,30,40,60,120} Эта функция работает и в области гауссовых чисел.
Divisors [24 + 301.]
(1,1+I,2,3,3+3I,4+5I,6,8+10I,9+11I,12+15I,24+30I,27+31I}
При необходимости нужно указать опцию Gaussianlntegers->True. Без этой опции делители натуральных чисел находятся только среди натуральных чисел.
Divisors[320]
{1,2,4,5,8,10,16,20,32,40,64,80,160,320}Если же указать эту опцию, то даже у натурального числа будут найдены все его делители в области гауссовых чисел.

Есть несколько важных числовых функций, связанных с делителями. Прежде всего это сумма k-x степеней всех делителей данного числа. Эта функция часто обозначается так: о", (n). При k = 0 получаем количество делителей t(n), а при k = 1 — сумму делителей 0(и). (В принципе совсем несложно получить и значения основных симметрических многочленов оn делителей, а значит, и составить алгебраическое уравнение, корнями которого являются делители заданного числа.) В системе Mathematica эта функция называется DivisorSigma [k, n].
Число делителей τ(n)
Давайте подсчитаем число делителей числа 360. Для этого можно просто вычислить длину списка делителей.
Length@Divisors[360]
24
Есть еще один способ. Можно найти сумму нулевых степеней делителей:
DivisorSigma[0,360]
24
Числа с заданным числом делителей
Существует единственное натуральное число n = 1, которое имеет только один делитель. Ровно два делителя имеют простые числа, и только они. (Они делятся на 1 и на себя.) Поэтому наименьшим числом, имеющим два делителя, является 2.
А какие числа имеют ровно 3 делителя? Если n = nmр-... рm-1 — каноническое разложение искомого числа, то т(л) = (m1+1) (m2+1) ... (mt+1). Если τ(n) = 3, то (m1-H) (m2+l) ... (mk+l) = 3. Поскольку 3 — простое число, то слева только один множитель может быть отличен от 1. Поэтому k = 1, а m =2. Поэтому ровно 3 делителя имеют квадраты простых чисел, и только они. Наименьшим числом с 3 делителями является, конечно, 4.
Так же легко найти и все числа, имеющие простое число делителей. Обозначим число делителей через τ(n) = q. Тогда (т,+1) (от2 +1) ... (mt +1) = q. Поскольку q — простое число, то слева только один множитель может быть отличен от 1. Поэтому k=l,aml = q— 1. Поэтому простое число делителей имеют степени простых чисел, и только в том случае, если показатель степени на 1 меньше простого числа. Наименьшим числом с простым числом делителей q является 2m1.
Теперь давайте найдем все числа, имеющие 4 делителя. В этом случае m(n) = 4 и (m,+l) (m,+l) ... (mt+l) = 4. Поэтому k<2. Если k= 1, то оm1 = 3, а если k = 2, то nm = 0m= 2. Поэтому ровно 4 делителя имеют кубы простых чисел и произведения двух различных простых чисел. Наименьшим числом с 4 делителями является, конечно, 6.
Наконец, давайте найдем все числа, имеющие 6 делителей. В этом случае m(n) = 6 и (оm,+1) (m, +1) ... (mt + 1) = 6. Поэтому k<2. Если k = 1, то оm1 = 5, а если k = 2, то оm =2, 1m = 1. Поэтому ровно 6 делителей имеют пятые степени простых чисел и произведения квадратов простых чисел на другое простое число. Наименьшим числом с 6 делителями является, конечно, 12.
В принципе этот метод можно использовать для вычисления наименьших натуральных чисел, имеющих заданное число делителей.
Впрочем, иногда легче отыскать такое число в таблице, указывающей количество делителей для различных чисел. Составить такую таблицу с помощью системы Mathematica не составляет труда.
Do[Print[n, ":",DivisorSigma[0,n]],
{n,k=50)]Но едва ли стоит иметь такую таблицу в напечатанном виде. Ведь в компьютерную эпоху поиск путем визуального просмотра нескольких сот страниц справедливо считается не наиболее легким решением. Проще модифицировать программу.
Пример 8.5. Наименьшее число, имеющее 14 делителей. Предположим, нужно найти наименьшее число, имеющее 14 делителей. Тогда программу можно модифицировать так.
m=14;
n=1;
While[DivisorSigma[0,n]!=m,n++];
Print[n, ":", DivisorSigma[0,n]]
Выполнив эту программу, получим результат.
192 : 14
Пример 8.6. Наименьшее число, имеющее 100 делителей. Предположим, нужно найти наименьшее число, имеющее 100 делителей. Тогда нужно выполнить следующую программу.
m=100;
n=1;
While[DivisorSigma[0,n]!=m,n++];
Print[n,":",DivisorSigma[0,n]]
Выполнив эту программу, получим результат.
45360 : 100
Честно говоря, здесь было немного риска. Ведь если бы числа с заданным числом делителей не оказалось, программа бы зациклилась. Но фокус в том, что всегда существует число, имеющее любое (натуральное, конечно) наперед заданное количество делителей.
Давайте, например, найдем все натуральные числа, количество делителей которых является произведением двух простых натуральных чисел.
Итак, пусть число делителей равно r s, где r и s — простые числа. Тогда n= рn-1 или n = pr-v > где p и n — произвольные простые числа.
Но, тем не менее, иногда программа, подобная приведенным выше, работает слишком долго. С ее помощью не удастся, например, за приемлемое время найти наименьшее число, имеющее миллион делителей.
Пример 8.7. Наименьшее число, имеющее миллион делителей. Известный немецкий популяризатор математики Вальтер Литцман в середине XX столетия писал, что согласно математическому бюллетеню Буэнос-Айреса в работе Мерсенна Cogitaeta physico-matematica, изданной в Париже в 1644 году, было указано, что наименьшее число, имеющее миллион делителей, есть
n=126765060022822940149670320537666-8472886094434.
Однако Вальтер Литцман заметил, что некоторые усомнились в этом и послали вопрос в Bolletino di Matematica (4-я серия, т. II, с. 28), было ли доказано это утверждение. Опять же, как сообщает Вальтер Литцман, ответ не был получен.
Давайте хотя бы частично проверим утверждение, сделанное в математическом бюллетене Буэнос-Айреса. Конечно, система Mathematica не может нам помочь проверить, действительно ли Мерсенн, а не кто-то другой нашел это число. Точно так же она не может нам помочь проверить, действительно ли в 1644 году, а не в каком-то другом было сделано это сообщение. Но зато система Mathematica может помочь при подсчете делителей этого числа.
nl=1267650600228229401496703205376;
n2=n!А66;
n3=847288609443; n4=n3А4; n5=n2*n4;
>DivisorSigma[0,п5] 666701
Как видите, миллионом здесь и не пахнет! Так что сомнения были не напрасными. Но опять же Вальтер Литцман указывает, что это число является 2028-значным. Это легко проверить.

Как бы не так! Тут аж 2035 цифр! Возможно, где-то прокралась опечатка. Но где? Вальтер Литцман указывает также, что число nl имеет 100 делителей. Проверим это.
DivisorSigma[0,nl]
101
Не волнуйтесь, с числом n1 все в порядке. Вальтер Литцман по традиции, восходящей к древним грекам, не учитывает при подсчете делителей само число. В отсутствии опечатки в числе легко убедиться.
FactorInteger [n1]
{{2,100}} Да это же сотая степень двойки! А что за зверь является основанием второго сомножителя? Не степень ли числа 3? Проверяем.
FactorInteger[n3]
{{3,25}} Так и есть! Теперь мы можем предположить, что Мерсенн указал число видаn-y. Чтобы найти х и у, достаточно решить уравнение (х+1)(у+1)-1 = 1000000 в натуральных числах. Приведем это уравнение к виду (х+1)ОН-1) = 1000001. Найдем каноническое разложение числа 1000001.
Factorlnteger[1000001]
{{101,1),{9901,1})Как видите, 1000001 = 101x9901. Так что либо х+1 = 101 и у+1 = 9901, либо jc+1 = 9901 и у+1 = 101. Иными словами, либо х - 100 и у = 9900, либо х = 9900 и у- 100. Как видим, вариантов не много. Все зависит от того, какое число меньше: 29900*3100 или 2100 - З9900. Конечно, 29900* 3100< 2100*З9900. Это очевидно, и тут Мерсенн ошибиться не мог. Так что х = 9900 и у = 100. Но это значит, что найденное Мерсенном число можно записать так: 29m-31m = (2100)"'(323)4. Так что опечатка, оказывается, в показателе степени: вместо 99 там указано 66. Если учесть технологию верстки книг до середины прошлого столетия (текст приходилось набирать в "перевернутом" виде), то нужно признать, что цифры 6 и 9 можно было запросто перепутать. Поэтому такая ошибка вполне вероятна. Давайте теперь проверим, что мы не ошиблись и найденное нами число действительно имеет миллион (не считая самого себя) делителей.
nl=1267650600228229401496703205376;
n2=n1А99;
n3=847288609443;
n4=пЗМ;
Сошлось, как в аптеке! Но беспокоит вот что: найденное нами число больше того, которое было указано Вальтером Литцманом. А указанное им число имело 2035 знаков, хотя он указал, что должно быть всего лишь 2048 цифр. Давайте посмотрим, какое число получилось у нас.

Это число имеет 3028 цифр! Ага, опять опечатка! А вдруг нет? Ведь мы еще не проверили, что найденное нами число наименьшее.
Пусть n = рm1 ,рm2...рmn — каноническое разложение искомого числа, причем в этом разложении простые числа записаны в порядке возрастания. Тогда τ(n) = (m1+1) (m+1)... (m1 + 1).
Так что (m1+l) (m1+l) ... (mt+1) = 101x9901. Поскольку о(и) = (mn + 1) (m1+1) ... (mt +1) не зависит от чисел pi, а только от показателей m1, m2, ..., mt, то наименьшее число и получится тогда, когда мы будем выбирать наименьшие возможные pi, т.е. должно выполняться условие р( = Prime [i]. (Иными словами, мы должны начать с наименьшего простого числа, а затем выбирать их по порядку. Так что pt = 2, 2 = 3 и т.д.) Так как число n - р™'р™...р™' наименьшее, то mi<m2<...mk. (В противном случае мы могли бы уменьшить число, переставив показатели m1 m2 ..., mk, что совершенно не повлияло бы на количество делителей.) Далее, поскольку (m, + 1)х x(m,+l) ... (mt+l) = 101x9901 и все множители в правой части простые, k<2. Если k = 2, то m1 = 2, рr = 3; все возможные варианты в этом случае мы только что исследовали. Если же k= 1, то р, = 2, но зато m = 1000000. Других вариантов в этом случае нет. Но 210СООО° имеет 301030 цифр.
IntegerPart[Log[10,2^1000000] ]
301029
Так что 21000000 > 29900 * 300. Итак, мы доказали, что наименьшим числом, имеющим
миллион (не считая самого числа) делителей, является 29900-3n10, имеющее 3048 цифр. Как видите, с помощью системы Mathematica мы провели полное исследование математической части сообщения, сделанного Вальтером Литцманом. Что же касается расследования по исторической части сообщения, то здесь я не могу похвастаться особыми успехами. Дело в том, как научный сотрудник, не связанный со спецслужбами, я не смог получить доступ к оригиналам работ Вальтера Литцмана. (Если вы не связаны с этими самыми спецслужбами, то вы хорошо знаете, что сотрудники "самой научной" библиотеки всегда найдут повод отказать вам в выдаче книги, которая, как кажется сотрудникам этих самых служб, может "недостаточно активно" восхвалять существующий строй. А тут зарубежные книги. Тем более популярные. Кто знает, что они там популяризируют?) Поэтому я видел работы Вальтера Литцмана только в переводе. Мне самому приходилось переводить различные книги, и я хорошо знаю, насколько пренебрежительно в некоторых издательствах относятся к словам автора. Особенно в советских. Там больше смотрели как бы чего не вышло, а далеко не за точностью передачи мысли автора и не за отсутствием опечаток в листингах. Опечатки в вышеупомянутом сообщении я обнаружил еще тогда, когда конструировал системы компьютерной алгебры. Но эти опечатки, конечно, я обнаружил в переводе. Вполне вероятно, что они были сделаны при печати перевода. Но ведь если бы в математическом бюллетене Буэнос-Айреса все было напечатано без опечаток, то почему в Bolletino di Matematica был направлен вопрос? В'чем было сомнение? В математических способностях Мерсенна? В энциклопедии Britannica сказано, что Мерсенн действительно публиковал работу Cogitaeta physico-matematica и издана она была в Париже в 1644 году. Там же сказано, что он был хорошо знаком с работами Ренэ Декарта, Блеза Паскаля, Галилео Галилея, Христиана Гюйгенса, Пьера Ферма... В 1635 году он основал (частную) Парижскую Академию Наук (Academic Parisienne), которая затем стала Академией Наук Франции... В чем, собственно, было сомнение? В том, что Мерсенн смог найти разложение 1000001 = 101x9901? При его-то энергии? В том, что Мерсенн знал формулу для числа делителей τ(n) = (m+1) (n +1) ... (mt +1)? Едва ли, без нее даже подсчитать число делителей было бы весьма трудно. Да и формулу для суммы делителей, очень похожую на формулу для количества делителей, вывели Пьер Ферма и Ренэ Декарт. Причем своими изысканиями в области дружественных чисел Пьер Ферма и Ренэ Декарт занимались независимо, хотя и пришли к тем же формулам, что и один из самых выдающихся арабских математиков абу-Хасан Сабит ибн Корра ибн Марван аль-Харани (836—901). Пьер Ферма сообщил Мерсенну о своем открытии правила Сабита в 1636 году (письмо Мерсенну датировано 24 июня), а Ренэ Декарт — в 1638 году (письмо Мерсенну датировано 31 марта), т.е. за 8 и 6 лет до выхода работы Мерсенна Cogitaeta physico-matematica. Так что наиболее вероятным мне кажется, что опечатки все же были не только в переводах или в работах Вальтера Литцмана... Если вспомнить, что в средние века в книгах слова печатались подряд, без пробелов, а математическая символика практически отсутствовала, то вполне вероятной выглядит версия об опечатке в показателе степени...
Пример 8.8. График количества делителей.
Теперь давайте построим график количества делителей. Сначала используем функции Table и DivisorSigma для построения таблицы tl (точнее, списка) количества делителей первых n чисел. tl= Table[DivisorSigma[0,k],{k,1,n=10^3}];
Теперь можем использовать функцию ListPlot для построения графика.
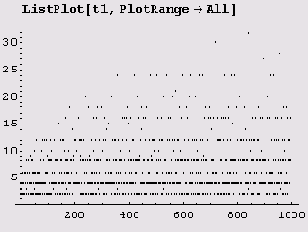
А вот график для n = 100000.

Обратите внимание, несмотря на то что большинство точек расположено весьма невысоко, отдельным точкам удается занять позицию, расположенную выше всех своих предшественников. Абсциссы этих точек являются сверхсоставными числами.
Сверхсоставные числа
Натуральное число и называется сверхсоставным, если у всех натуральных чисел, меньших п, количество делителей меньше, чем у я. Первым сверхсоставным числом является 1 просто потому, что у него нет предшественников. (Парадокс терминологии: 1 является сверхсоставным числом, но не относится к составным. Вторым, конечно, идет 2, третьим — 4, четвертым — 6, пятым — сразу аж 12. Ну а как найти /п-е сверхсоставное число? Вот нужная нам функция.
SuperComposite[m_]:=
Module[{t=l,tmax = l,n=1, n0=l),
While[n<m,{nO++,t = DivisorSigma[0,nO],
If[tmax<t,{tmax=t,n++}]}] ;nO]
Вот как с помощью этой функции можно составить таблицу первых m сверхсоставных чисел.
tl= Table[SuperComposite[k],{k,l,n=m}]
Однако у этой программы есть существенный недостаток: поиск в ней организован весьма неэффективно. Ведь программа для поиска очередного сверхсоставного числа повторяет все вычисления, выполненные для поиска всех предшествующих сверхсоставных чисел. Поэтому она ищет очередное сверхсоставное число слишком медленно. Для составления списка сверхсоставных чисел лучше использовать другую программу.
Module[{t=l,tmax = l,n=l, n0=l, m=10000},
While[n<m,{n0++,t = DivisorSigma[0,n0],
If[tmax<t,{tmax=t,n++, Print[n, ":", nO]}]}]]
В составленной по результатам выполнения программы таблице для каждого сверхсоставного числа указано количество и сумма делителей, а также его каноническое разложение.
Заметьте, что в каноническом разложении сверхсоставных чисел простые числа следуют без пропусков (т.е. за Prime [i] в каноническом разложении следует Prime [i+1], а не большее простое число), а показатели степеней — в невозрастающем порядке. Все сверхсоставные числа, за исключением 1, четные. Начиная с четвертого все они делятся еще и на 3 и потому кратны 6. Начиная с пятого все они делятся не только на 2, но и на квадрат двойки, т.е. на 4, и потому кратны 12. Но не думайте, что если n-е сверхсоставное число делится на простое число р, то и все последующие сверхсоставные числа будут делиться на это простое число р. 25-е сверхсоставное число делится на простое число 11, а 26- и 27-е сверхсоставные числа на 11 не делятся. Потом, правда, 11 опять появляется в каноническом разложении. Так что вы, возможно, склонны считать это исключением или аномалией. Но в таком случае придется признать, что это исключение (или аномалия — как вам больше нравится?) не единичное. Ведь 53-е сверхсоставное число делится на простое число 17, а 54-е сверхсоставное число на 17 не делится. В данном случае, правда, аномалия еще короче: 17 появляется в каноническом разложении уже 55-го числа. Как вы думаете, для всякой ли степени данного простого числа найдется такое сверхсоставное число, что все последующие за ним сверхсоставные числа делятся на эту степень данного простого числа? Если вам это очевидно, то заметьте, что из этого немедленно следует, что все сверхсоставные числа, начиная с некоторого, номер которого, конечно, зависит от заданного натурального числа, делятся на это заданное натуральное число. Действительно уж, сверх-составные — антиподы простых! Впрочем, все эти свойства в нашей программе не учитываются. (В программе не учитывается даже, что сверхсоставных чисел бесконечно много.) Зато эту программу легко модифицировать так, чтобы поиск сверхсоставного числа можно было продолжить начиная с любого ранее найденного. Вот как, например, можно продолжить поиск сверхсоставных чисел после 64-го.
Module[{t=l,tmax = 1200,n=64, n0=551350800, m=10000},
While[n<m,{n0++,t = DivisorSigma[0,n0],
If[tmax<t,{tmax=t,n++,Print[n,":", n0]}]}]]
Тем не менее, нужно заметить, что гораздо более эффективно поиск сверхсоставных чисел можно было бы организовать по их каноническому представлению или же с применением решета, основанного на нахождении чисел, имеющих заданное число делителей. Методы решета позволили бы сразу вычеркнуть из таблицы большинство чисел, поскольку, как мы видели на графике, большинство чисел имеют совсем немного делителей. Ведь при больших n на долю каждого из первых n натуральных чисел в среднем приходится лишь Inn делителей.
Сумма делителей σ(n)
Давайте найдем сумму делителей числа 360. Для этого можно просто просуммировать все элементы списка делителей.
Plus@@Divisors[360]
1170
Есть и еще один способ. Можно найти сумму первых степеней делителей.
DivisorSigma[1,360]
1170
Пример 8.9. График суммы делителей.
Давайте теперь построим график суммы делителей. Сначала мы используем функции Table и DivisorSigma для построения таблицы tl (точнее, списка) сумм делителей первых n чисел.
t1= TabletDivisorSigma[l,k],{k,l,n=10A3}];Теперь можем использовать функцию ListPlot для построения графика.

А вот график для n = 100000.

Обратите внимание на то, что все точки графика расположены не ниже прямой у = х, поскольку в сумму делителей включается и само число. Если же само число не включать в сумму делителей, то программа и графики будут несколько иными.

А вот график для n = 100000.
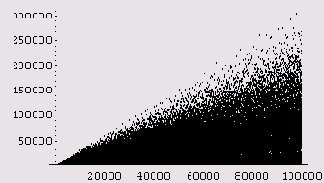
Ниже приведен также график функции у = σ(n)/n.

Интерес представляет также график функции у = σ(n)/(n In n).
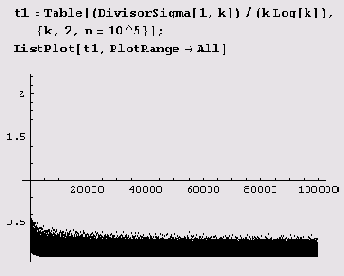
Недостаточные, избыточные, совершенные и дружественные числа
Нумерология (или гематрия, как ее еще иногда называют) была распространенным увлечением у древних греков... Делители или аликвотные части играли важную роль в нумерологии.
Поскольку в Древней Греции числа изображались буквами греческого алфавита, каждому написанному слову, каждому имени соответствовало некоторое число. А раз так, можно было сравнивать свойства чисел, соответствующих именам людей, со свойствами (характером) человека. Было сходство или нет, достоверных исторических сведений нет, а вот о свойствах чисел, как мы уже не раз убеждались, есть сведения вполне достоверные, хотя и далеко не полные. Идеальными греки считали совершенные числа, т.е. натуральные числа, равные сумме своих натуральных делителей, меньших самого числа. (Здесь следует отметить, что древние греки не считали само число его делителем.) В некоторой степени это можно понять. Ведь если натуральное число равно сумме своих натуральных делителей, меньших самого числа, то можно сказать, что оно равно сумме своих аликвотных частей. Перенесите это свойство на человека. Получится, что человек с этим свойством как бы самодостаточный, он сможет, подобно Робинзону, преодолеть длительную разлуку с родными, друзьями, сможет преодолеть все стихии. (Ведь такой человек "равен сумме своих частей".) Конечно же, поиску совершенных чисел уделялось огромное внимание. Но мы не станем останавливаться на этом, поскольку, как доказал Эйлер, всякое четное совершенное число имеет вид p = 2n-1-Мр, где Мp =2p -1 — простое число Мерсенна. О том, что числа такого вида являются совершенными, писал еще Евклид в IX книге "Начал". Так что каждое простое число Мерсенна порождает четное совершенное число. И, конечно же, наибольший простой делитель каждого четного совершенного числа является простым числом Мерсенна. Так что в некотором роде мы о четных совершенных числах знаем столько же, сколько о простых числах Мерсенна. Что же касается нечетных совершенных чисел, то тут вполне уместен вопрос: а разве совершенные числа бывают нечетными, разве идеал может быть нечетным? Ответ на этот вопрос до сих пор неизвестен. Не попытаться ли найти его с помощью системы Mathematica? Вполне возможно, что система Mathematjca может помочь найти ответ и на этот вопрос. Но пока лобовой атакой, даже при поддержке системы Mathematica, крепости Нечетных Совершенных Чисел не удастся не только взять, но и даже дойти до нее. Ведь как показал автор одного из лучших учебников классической теории чисел Александр Адольфович Бухштаб, наименьшее нечетное совершенное число, если оно существует, имеет не менее двух с половиной тысяч цифр (в десятичной системе счисления). Для прямого перебора всех нечетных чисел это слишком много. Впрочем, всегда были смельчаки, которые пытались перебирать нечетные числа, используя те или иные дополнительные ухищрения. Еще в 1968 году Брайен Такерман из IBM подобрался, например, к 36-значным числам. К 1977 году всевозможные ухищрения позволили отбраковать все числа до 1050. Если нечетные простые числа существуют, то они имеют не менее 2800 различных простых множителей и имеют вид p4t+1 N2, где р — простое число вида 4n+l, a # взаимно просто с р. Давайте же уточним нижнюю оценку количества цифр в наименьшем нечетном совершенном числе. Как только что было сказано, такое число содержит не менее 2800 различных простых множителей, причем все они, кроме, возможно, одного, входят в степени не ниже 1. Поскольку рассматриваемое число нечетное, то 2 среди этих простых чисел отсутствует. Значит, чтобы получить нижнюю границу, мы можем возвести в квадрат произведение 2800 простых чисел рr = 3, Р3 = 5, ..., рrm = 25409 и разделить ее на наибольшее число в этом произведении, т.е. на р[n] = 25409. С системой Mathematica нет проблем.

Конец я опустил, потому что в полученном результате 21 892 цифры.
IntegerPart[Log[10,nn]]
.21891
Это результат, которого еще никому не удалось достигнуть! Хотя вычисленное нами число имеет вид р4М -N2, оно не совершенное, так как сумма всех его делителей, не считая самого числа, является числом, имеющим 21 893 цифры.
IntegerPart[Log[10,DivisorSigma[l,nn]-nn]]
21892
Значит, сумма всех делителей этого числа, не считая самого числа, больше самого числа. Число, сумма всех делителей которого, не считая самого числа, больше самого числа, называется избыточным. Иными словами, число п называется избыточным, если о(n)>2n. Честно говоря, несколько удивительно то, что это число оказалось избыточным. Сейчас объясню, почему. Давайте найдем все избыточные нечетные числа, меньшие 100 000. Вот нужная нам программа.

Как видите, первым нечетным избыточным числом является 945. А избыточных нечетных чисел, меньших 100 000, всего 210. Это очень мало! Так что нам очень повезло: первое встреченное нами число оказалось избыточным нечетным. Остальные нечетные числа, меньшие 100 000, являются недостаточными. (Число, сумма всех делителей которого, не' считая самого числа, меньше самого числа, называется недостаточным. Иными словами, число л называется недостаточным, если о(n)<2и.) Как много бедных, как мало богатых... Ох, простите, я хотел сказать как много чисел недостаточных, как мало избыточных среди нечетных чисел, меньших 100 000. Если через А(х) обозначить число избыточных чисел, меньших или равных х, то 0,1241х<^(х)<0,314х, так что большинство чисел является недостаточным. Хотя существование предела отношения
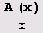
А может ли последовательность х0 = a, n, = σ(n)-n, ..., xn+1 = σ(xn)-nr1, ... иметь период? Ведь если бы такое случилось, то, с точки зрения древних греков, этот период был бы "самодостаточным"! Известны случаи, когда эта последовательность вообще постоянна. Конечно, это происходит в том случае, если л — совершенное число. Но совершенных чисел так мало, а опасных, дальних дорог (хотя бы за золотым руном) так много! На все дороги не напастись совершенных чисел. Может быть, в такие дальние путешествия можно отправлять не только совершенные числа, но и периоды из таких последовательностей? С точки зрения древних греков, думаю, неплохая идея. Но длинные периоды — многочисленные экипажи. А для многочисленных экипажей нужны очень большие суда. Другое дело постоянные последовательности. У постоянных последовательностей длина периода равна 1. Но эти последовательности встречаются, как мы знаем, весьма редко. (Только отчаянные смельчаки могут рискнуть отправиться в дальнее одиночное плавание.) К тому же неизвестно, бесконечно ли их число. Затем идут последовательности, у которых длина периода равна 2. Есть ли такие? Период таких последовательностей состоит всего из двух чисел, таких, что сумма делителей одного числа равна другому (напомним, что сами числа при подсчете суммы не учитываются). Фактически такой период является идеальной "супружеской" парой, в которой недостаток "чувств" (слагаемых) одного "супруга" (числа) компенсируется избытком "чувств" (слагаемых) другого. Такие пары чисел называются дружественными. Иными словами, пара (а, b) различных натуральных чисел афЬ называется дружественной, если о(n)—а = b, a a(b)—b — а. Увы, грекам не повезло: они знали лишь одну дружественную пару: 220 и 284. Лишь в 1636 году (письмо Мерсенну датировано 24 июня) Пьеру Ферма удалось найти еще одну: (17296, 18418). А сколько сможем найти мы? С помощью системы Mathematica, разумеется. Попробуем. Сначала определим функцию, определяющую, есть ли у избыточного числа а недостаточный "супруг". Заметьте, что избыточное число всегда меньше своего недостаточного "супруга". Вот нужная нам функция.
Friend[n_]:=Module[ft},
If[(t=DivisorSigma[1,n]-n)>n,
If[DivisorSigma[1,t]-t==n,t,0],0]]
Эта функция находит большего (значит, недостаточного) "супруга", если он есть, и "рекомендует" число 0, если большего "супруга" нет. Осталось определить, что мы будем печатать, и запустить перебор. Давайте печатать номер найденной пары, ее избыточное (меньшее) число, его каноническое разложение, а затем недостаточное (большее) число и его каноническое разложение.
prn:=Print[n,":",а,":",FactorInteger[a],":",b,":",
FactorInteger[b]]
Запускаем перебор.
For[n=0;а=1,а<10^7,a++,If[(b=Friend[a])>0,n++;prn]]
Результаты перебора оформляем в виде таблицы.
Как видно из таблицы, в пределах первой тысячи есть только одна дружественная пара (220, 284) — та, которую знал еще Пифагор! В пределах первых десяти тысяч есть всего лишь 5 дружественных пар, а в пределах первых ста тысяч их только 13. Не удивительно, что поиск, дружественных чисел напоминал охбту за редкой дичью. Недостижимым чемпионом долгое время был Эйлер. Его рекорд побил бельгиец Поль Пуле, который в Брюсселе в 1929 году издал двухтомную монографию по теории чисел под многозначительным названием "La chasse aux nombres" ("Охота за числами"). Кроме всего прочего, в ней приведены 62 новые пары дружественных чисел. Пуле (как ранее Лежандр и Чебышев) пошел по пути открытия новых критериев простоты чисел. Значительная часть его исследований посвящена развитию идей французского математика Люка, открывшего в высшей степени эффективные критерии простоты.
Новый "мировой рекорд" установил американец Э. Эскотт, а затем рекорд перешел к его соотечественнику Элвину Дж. Ли. По существу, они также пользовались методами Эйлера, хотя и в усовершенствованной форме. Правда, Ли нарушил правила спортивного соревнования — он был первым, кто прибегнул в столь больших масштабах к помощи ЭВМ. Зато он нашел 390 дружественных пар! Весьма любопытна таблица "чемпионата" .
Наконец, использованный нами метод перебора был применен в Йельском университете на IBM 7094, — там были проверены все числа до миллиона, и было обнаружено, что в пределах миллиона имеется всего 42 дружественные пары. При этом были найдены (в небольшом количестве, правда) ранее неизвестные пары.
С наступлением эры ЭВМ появилась новая возможность, о которой Эйлер не мог и помышлять, — заставить машину перебирать все числа подряд, пока хватит машинного времени. Конечно, нашлись люди, которые только и ждали, когда появится возможность производить громадные вычисления. Они занимались ими в течение двух лет, не считаясь с затратами, и добрались до десятизначных чисел. (По некоторым сведениям еще до 1968 году путем перебора с некоторыми ухищрениями поиски пар дружественных чисел разной четности были проведены до трех миллиардов, но результатов не дали.) Некоторые квалифицировали это как грубый нажим конкурентов на таких тонких и искусных ловцов чисел, какими были Эйлер, Пуле и Ли. Как к этому относиться? Блюстители "чистоты" спортивных соревнований даже сравнивают тонких и искусных ловцов со страстными рыболовами-любителями, неожиданно замечающими у ручья людей, которые просто осушают русло и затем спокойно собирают рыбу! Впрочем, при этом обнаружилось, что рыболовы удили весьма успешно и выловили почти всю рыбу, так что "браконьерам" досталась лишь довольно скромная добыча. Впрочем, те из блюстителей чистоты спортивных традиций, которые сами были успешными рыболовами, сознались, что они тоже... Нет, упаси Боже, они не подходили к пульту ЭВМ, они просто просили (я бы сказал истошно взывали) других людей найти простые числа в довольно длинной последовательности чисел определенного вида...
Как же получилось так, что дружественные пары открывались не последовательно, а "вразброс"? Почему после пары Пифагора (220, 284) Пьер Ферма нашел пару (17296, 18418), пропустив, как видно из нашей таблицы, сразу 6 пар?'Оказывается, Пьер Ферма (и Ренэ Декарт) открыли способ получения дружественных чисел (правило), который знал арабский математик, врач и астроном Сабит (тот самый абу-Хасан Сабит ибн Корра ибн Марван аль-Харани) еще в IX веке. Этот способ получения дружественных чисел звучит на современном языке так.
Теорема Сабита. Если все три числа р= 3-2n-1-1, q= 3-2n-1 и r-=9-22n-1-1 — простые, то числа А- M *p-q и 5 = Т *rr — дружественные.
При n = 2 получается пара чисел, найденная Пифагором. Однако теорема Сабита дает дружественные числа и при других п, например при n = 4 и n = 7. С помощью "вульгарного" применения ЭВМ блюстители чистоты спортивных традиций обнаружили, что этими тремя случаями исчерпываются все значения и<20 000, при которых все три числа р = 3-2n-1—1, q= 3-2n-1 и r= 9*22n-1-1 — простые. Иными словами, для и<20 000 указанный способ дает дружественные числа только при n = 2, n = 4 и n = 7. Использовал ли сам Сабит свою теорему для отыскания дружественных чисел при я>2, неизвестно. Открытие второй (n = 4) и третьей (n = 7) пар дружественных чисел приписывалось ранее Ферма и Декарту соответственно. Однако в одном из трактатов марокканского ученого ибн аль-Банны (1256—1321), сына архитектора, были обнаружены следующие строки: "Числа 17296 и 18416 являются дружественными; одно из них избыточно, другое недостаточно. Аллах всеведущ".
С течением времени формулы, предложенные Сабитом, были забыты, а его книгу открыли заново лишь в XIX веке. Впрочем, многие античные и арабские ученые, а также ученые средневековья посвящали в своих трактатах одну из глав совершенным и дружественным числам. Однако большей частью в этих трактатах было мало новых сведений и много ошибок. Правда, очень удивляет то поразительное единодушие, с которым авторы этих сочинений настаивают на возможности практического использования дружественных чисел. Например, ибн Хальдун прилагает к своему трактату руководство по изготовлению талисмана дружбы, а мадридский ученый аль-Маджрити (ум. в 1007 г.) приводит рецепт, позволяющий добиться взаимности в любви: надо записать на чем-либо числа 220 и 284, меньшее дать съесть предмету страсти, а большее съесть самому; ученый добавляет, что действенность этого способа он проверил на себе.
Пьер Ферма в 1636 году и Ренэ Декарт в 1638 году независимо друг от друга вновь открыли формулы Сабита. О датах и обстоятельствах этих открытий имеются самые точные сведения, потому что Ферма и Декарт написали Мерсенну, который в предисловии к своей ближайшей книге (Les nouvelles pensees de Galilee (1639)) назвал их открытие крупным достижением гениальных математиков. (Между прочим, в ходе своих исследований Ферма и Декарт вывели формулу, дающую сумму делителей числа по его представлению в виде произведения степеней простых чисел. Можно ли сомневаться, что Мерсенн ее знал?)
Так вот, Вальтер Боро, один из тех весьма удачливых рыбаков, что сознались в том, что просили других вычислителей (Херман те Риле был наиболее удачливым из них) посчитать кое-что на ЭВМ, придумал вот что. Раз способ Сабита дает столь мало дружественных пар, значит, нужно придумать целую серию таких правил. С этой целью он придумал свой рецепт.
Рецепт Вальтера Боро. Если для пары дружественных чисел вида А= а-n и В = a-s числа s и р = n + s+l являются простыми, причем а не делится на р, то при всех тех натуральных и, при которых оба числа qt = (n + 1)рn+> -1 и nr= (u + l)(s + 1)р"-I просты,числа В1 = N//</, и Вr = apn*q2 —дружественные.
Рассмотрим пример применения правила. Возьмем пару Пифагора: А = 220 = 22-55 и 5= 284= 22-71. Положим а = 22, и = 55, s =71.
Числа s = 71 и р = n + s+ 1 = 55 + 72 = 127 — простые. Поэтому можно использовать указанное правило. При n= 1 числа <?, = (м + 1)р"+1-1 и <?2 = (u + l)(s + l)pa-1 не являются простыми, но уже при n = 2 мы получаем пару дружественных чисел В, = 220-1272-903223, В, = 4-1272-65032127.
Эти довольно большие числа, полученные из пары (220, 284) почти без всяких вычислений, не были известны до открытия "рецепта"!
Еще один пример. Возьмем пару Эйлера А = З4*5 * 11 * 29* 89 = а *n и В= 3n-5-11-2699 = a*s.
Здесь также числа s = 2699 up=u + s+l = 5281 являются простыми. Таким образом, по этой паре Эйлера тоже можно построить соответствующее "правило Сабита-Боро". В этом случае уже при a= 1 числа <?, = (n + 1)Mn-1-1 и q2 = (u + l)(s + l)pa-1 будут простыми, и мы получаем дружественные числа
В1 = 34-5-11-29-89-5281-13635541,
В2 = 34-5-11-5281- 36815963399.
Рецепт работает! Но как его нашел Вальтер Боро? Он решил искать дружественные пары, в которых оба числа имеют вид Bl-b1-pn-q1 с простыми р, q, и <?, (1= 1, 2). Иными словами, выбираются и фиксируются три числа B1, B2,р,и при каждом n - 1, 2, 3, ... ищутся N и Nr. Поскольку В1 и В2 — дружественные числа, то а( В,) = В, + В2 = о( В2), откуда следует, что
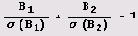
Теперь, вспоминая, что сумма делителей мультипликативна, т.е. а(ху) = а(х)а(у) для взаимно простых х и у, причем

(р — простое), получим:
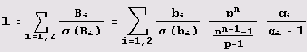
Замечаем, что при n числа n и M, также стремятся к бесконечности. Таким образом, переходя в последнем равенстве к пределу при n->-1, получаем основное уравнение
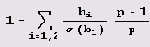
Это соотношение связывает три числа q1,q2 и p, которые следует подставлять в исходную формулу Bi=bi*pn*qi. Отыскивая простейшие решения основного уравнения
 1= 220, B2= 4и из основного уравнения найдем для р значение 127. Тем самым мы получим ранее наиденную пару B1=220.1272 903223 и B2=4*1272 *65032127 .
1= 220, B2= 4и из основного уравнения найдем для р значение 127. Тем самым мы получим ранее наиденную пару B1=220.1272 903223 и B2=4*1272 *65032127 .Правда, вначале одно из больших чисел ,, и ь все время оказывалось составным. Но второго октября 1972 года Херман те Риле сообшил, что по Формуле приведенной в качестве примера для пары Эйлера А - 3 -5.11-29-89 -а ы и 5 =34-5-11-2699 = а-5, при я = 19 получаются числа 9|=(« + 1)Р 1 и а -(« + 1)(,+1)/-1 по меньшей мере псевдопростые (под псевдопростьш числом здес2ь подразумевается такое число ,. для которого выполняется сравнение малой теоремы Ферма.
Число А имеет 800 различных делителей, а число В — 3200.
DivisorSigma[О,А]
800
DivisorSigma[О,В]
3200
Простым перебором эту пару, конечно, не найти. Система Mathematica позволяет в мгновение ока найти канонические разложения чисел этой пары.
Ну, теперь хоть можете узнать те сомножители, которые эта пара "заимствовала" у пары Эйлера? Без системы Mathematica их бы без усилий не найти!
с важными числовыми функциями мы
В этой главе знакомство с важными числовыми функциями мы начали с функции Эйлера ф(m), дающей количество классов приведенной системы вычетов. Эта функция удовлетворяет сравнению a*1n-1 =l(modm). Однако наименьшее натуральное число, удовлетворяющее сравнению ax=1l(modm) для всех а, взаимно простых с т, доставляет функция Кармайкла λ(m). Эти функции связаны с каноническим разложением аргумента. По каноническому разложению аргумента легко также вычисляется и функция Мебиуса µ(x), отличная от нуля только в том случае, если ее аргумент свободен от квадратов, т.е. представляет собой произведение (возможно, пустое) различных простых чисел. Наконец, рассматривая функции, связанные с каноническим разложением аргумента, мы особо выделили функции, связанные с делителями. Функция Divisors позволяет найти все делители числа, а функция DivisorSigma — сумму k-x степеней всех делителей σ(n). При k = 0 получается количество делителей τ(n), а при k = 1 — сумма делителей σ(n). Изучая случай k = 0, т.е. количество делителей т(/г), мы обратили внимание на сверхсоставные числа. Рассматривая же случай k = 1, т.е. сумму делителей τ(n), мы нашли, что числа бывают недостаточные, избыточные, совершенные и дружественные. Но даже обсудив совершенные числа и дружбу между числами, мы решили далеко не все задачи элементарной теории чисел. (Сальвадор Дали сказал бы: мы не достигли совершенства.) Но эта книга предназначена для первого (хотя и серьезного) знакомства с системой Mathematica. И потому пришло время обратить свой взор не только на дружбу чисел, но и на те разделы математики, с которыми так дружна теория чисел. Иными словами, на все остальные разделы математики. И раз уж мы вспомнили об искусстве, предварим свое знакомство с возможностями системы Mathematica в других разделах математики коротеньким разговором об искусстве построения графиков.