Алгебра и пакет Mathematica 5
         

в своем историческом развитии повторяет



Компьютерная графика в своем историческом развитии повторяет путь аналитической геометрии. Когда-то давно', когда возникла аналитическая геометрия, т.е. во времена Пьера Ферма и Ренэ Декарта, она мыслилась в основном как аналитическая геометрия на плоскости (а зачастую даже как аналитическая геометрия в первом квадранте). Это был способ изучения плоских образов (кривых) с помощью метода координат на плоскости. Распространение методов аналитической геометрии на пространственные образы (линии и поверхности) было сделано столетием позже французским математиком Клеро (1713—1765). Облик, близкий традиционному, придал аналитической геометрии Леонард Эйлер в 1748 году, посвятив ей второй том "Введения в анализ". Однако еще более столетия курс аналитической геометрии делился на два раздела: аналитическая геометрия на плоскости и аналитическая геометрия в пространстве. Лишь в 60-е годы XX века в мехматовских учебниках мало-помалу исчезло это деление, сохранившееся в учебных планах педагогических институтов кое-где и по сей день. Впрочем, более чем за три десятилетия до конца XX века были сделаны (в основном, Анатолием Ивановичем Мальцевым и Алексеем Васильевичем Погоре-ловым) первые попытки преподавания многомерной аналитической геометрии, логическим завершением которых стали многочисленные (в 80-х годах XX века) объединенные курсы аналитической геометрии и линейной алгебры.

Нечто подобное наблюдается и в компьютерной графике. Поначалу графические редакторы (притом с весьма ограниченными возможностями) были предназначены для вычерчивания весьма ограниченного набора графических примитивов (в основном, точек и отрезков) на плоскости. Несколько позже набор графических примитивов был значительно расширен. Затем появились графические операции для изображения трехмерных образов, потом было добавлено еще одно измерение — время. Так в графические редакторы вошло движение и появилось компьютерное немое кино, которое почти сразу же обрело звук и тем самым превратилось в полноценное мультимедиа. Говорят, что пространство запахов оказалось 33-мерным, и вскоре в кинотеатрах и в компьютерах появятся устройства для воспроизведения запахов. С другой стороны, многие средства, впервые появившиеся в графических редакторах, впоследствии были встроены и в программы, первоначально вовсе не предназначавшиеся для художников. В систему Mathematica, например, встроены все средства мультимедиа, кроме отображения 33-мерного пространства запахов. Вы можете, например, увидеть и послушать синус, тангенс, ^-функцию Римана... (Трудно передать словами чувства, возникающие при прослушивании некоторых функций. Скажу лишь, что сбегались все домашние, чтобы посмотреть, что за зверь в компьютере издает такие звуки...) Но пока что средства воссоздания пространственных трехмерных образов лишь проектируются, и потому экраны всех компьютерных мониторов двухмерные (обычно плоские). И по этой причине наиболее простыми графическими примитивами являются те, которые предназначены для отображения плоских образов. Потому знакомство с графическими возможностями современных программ следует давней традиции, возникшей в курсах аналитической геометрии: сначала изучается аналитическая геометрия на плоскости... Ох, простите, я хотел сказать средства 2О-графики, т.е. средства изображения плоских образов (точек, кривых и других плоских фигур) с помощью метода координат на плоскости. И опять, по той же традиции основательному курсу аналитической геометрии на плоскости предшествует небольшое введение в основы метода.

Введение, или основные графические примитивы



График — это некоторый объект, с которым можно выполнять определенные операции, главнейшей из которых является отображение. Фактически двух- и трехмерные рисунки состоят из графических примитивов, таких как точки, линии, многоугольники, круги, диски, параллелепипеды и даже текст. Некоторые из этих примитивов являются составными, они сами состоят из других объектов. Например, линия есть на самом деле ломаная линия, состоящая из отрезков прямых, соединяющих последовательные угловые точки этой линии. Точка двухмерного рисунка как графический примитив есть выражение вида Point [ [х, у]}, где х и у суть декартовы координаты точки на плоскости.

Графические примитивы и их отображение на экране





Графический примитив и его изображение — разные вещи. Как же отобразить графический примитив на экране? Разберемся в этом на примере следующих двух графических примитивов: точки р = Point[{1,1)1 и линии 1 = Line[{{0,0}, {1/2,2}, {3/2,2}, {2,0}}].

Превратить их в рисунок на экране дисплея можно следующим способом. Сначала к ним нужно применить функцию Graphics, которая превратит их в один из шести графических объектов (Graphics, Density/Graphics, ContourGraphics, GraphicsSD, SurfaceGraphics или GraphicsArray). Полученный результат уже можно отобразить на экране с помощью функции show.

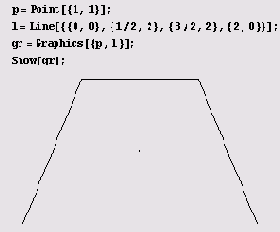
Конечно, я показал все промежуточные шаги. На самом деле все можно было сделать за один шаг.

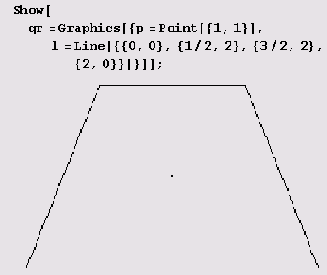
Присваивания, конечно, тоже не обязательны, но я хотел показать, что с результатами функций, используемых для задания графических примитивов, можно обращаться так же, как и с любыми другими.

Точка — графический примитив Point

Поворотным пунктом в изобразительном искусстве была Декартова переменная величина. Благодаря ей в изобразительное искусство вошли движение и тем самым эклектика, и благодаря этому в изобразительном искусстве революция, о необходимости которой так долго не говорили только те, кто ее не хотел, свершилась. Теперь рисовать может каждая кухарка.

Основоположник искусства расстановки точек на экране

Для представления точки служит графический примитив Point [coords], где coords— координаты точки. Они могут быть представлены либо в виде {х, у] или Scaled[{х, у}] в случае плоскости, либо в виде {х, у, z} или Scaled! {х, у, r)} в случае пространства. На экране точки, конечно, изображаются в виде кружков, радиус которых задается графическим примитивом Pointsize. Для раскраски точек используются параметры CMYKColor, GrayLevel, Hue и RGBColor.

Ломаная линия — графический примитив Line

Ломаная линия, соединяющая точки /я,, pt2, рц, ..., представляется графическим -примитивом Line [ { pt, , pt-, , pt}, ,...}]. Здесь pt, — координаты точки. Представленные ниже два выдающихся произведения изобразительного искусства созданы исключительно из двух серий однозвенных ломаных (отрезков прямых). Они оба называется скромно — муар.

 

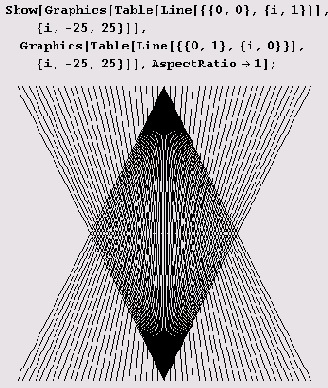
Муар — это, можно сказать, важный технический прием. Подбирая параметры, с его помощью можно создать достаточно замысловатый образ.


Графические директивы



Кроме графических примитивов, имеются графические директивы, определяющие опции представления примитивов на экране, такие как размер, цвет и стиль. Если они не указаны явно, то устанавливаются по умолчанию.

Относительная и абсолютная величина диаметра круга, изображающего точку, — директивы PointSize [d] и AbsolutePointSize[d]

Директивы PointSize [d] и AbsolutePointSize [d] определяют относительную и абсолютную величину диаметра круга, изображающего точку. В директиве PointSize [d] аргумент d есть отношение диаметра к ширине графика, и потому он обычно задается как дробь. По умолчанию d = 0.008 для двухмерных графиков и d = 0.001 для изображений трехмерных объектов. Вот график, в котором этот параметр задан по умолчанию.

А вот тот же график с иным значением этого параметра.

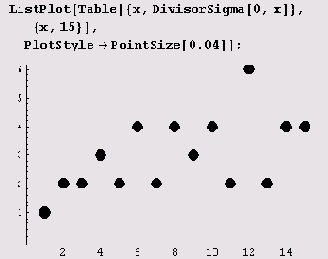
Точки теперь такие жирные, что одна даже не влезла в область, отведенную для графика!

В директиве AbsolutePointSize[rf] значение параметра d определяет диаметр круга в единицах длины, приблизительно равных одной семьдесят второй дюйма. Вот как может выглядеть парабола.

Как видите, директива ставится перед примитивом, и оба эти объекта заключаются в фигурные скобки. Кроме того, директива может действовать на несколько однородных примитивов, стоящих за ней. Вся группа также заключается в фигурные скобки. Графических директив может быть несколько, и они должны предшествовать тем примитивам, на отображение которых они должны влиять. Вычисление выражения

Show[Graphics[{PointSize[0.03],Hue[0],

Table[Point[{O.lj,0.05j}], {j,10}]}]];

приводит к появлению на экране десяти точек красного цвета относительного диаметра 0.03.

Относительная и абсолютная толщина линии — директивы Thickness и AbsoluteThickness

Как и в случае точек, управлять можно не только цветом, но и толщиной линии. Директива Thickness [r] определяет относительную ширину линии, а директива AbsoluteThickness [r] — абсолютную ширину. Вот пример указания относительной ширины линии.

Ниже приведен пример указания абсолютной ширины линии.

Пунктиры, штрихпунктиры и другие стили линии — директива Dashing

Директива Dashing [{rl, r2, ...}] позволяет указать, что линия рисуется в виде последовательности отрезков длиной rl, r2 и т.д., которые повторяются циклически. Вот как можно нарисовать окружность.

А вот параллельные прямые, нарисованные черточками разной длины.


Аналитическая геометрия на плоскости, или 2D-графика



Более чем за 100 лет до н.э. греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести хорошо теперь известные географические координаты: широту и долготу — и обозначить их числами.

В XIV в. французский математик Н. Оресм ввел, по аналогии с географическими, координаты на плоскости. Он предложил покрыть плоскость прямоугольной сеткой и называть широтой и долготой то, что мы теперь называем абсциссой и ординатой.

Это нововведение оказалось чрезвычайно продуктивным...


Графические примитивы



Графические примитивы в графике играют ту же роль, что и основные фигуры в геометрии. Именно из них составляются все остальные фигуры.

Многоугольник — примитив Polygon

Графический примитив Polygon! {{х1, y1], (х2, у2}, ...}] представляет собой закрашенный многоугольник, ограниченный замкнутой ломаной линий, проходящей через точки {х1, y1}, {х2, у2), .... Вот как рисуется равносторонний треугольник салатного цвета.

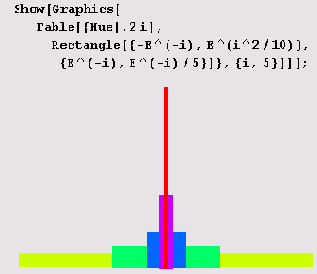
Прямоугольник — примитив Rectangle

Частный случай многоугольника — прямоугольник — можно получить с помощью примитива Rectangle [{xmin, ymin}, {хmах, уmах} ], в котором (xmin, ymin} — координаты левого нижнего угла прямоугольника, а {хmах, уmах} - координаты правого верхнего угла прямоугольника. Показанная ниже фигура состоит из пяти прямоугольников. Все они имеют разный цвет.

Окружности, эллипсы, их дуги, диски и сектора Окружность и ее дуга — примитив Circle

Дугу окружности создает графический примитив Circlet {х, у}, r, {thl,th2}]. Здесь {х,у} — координаты центра окружности, г — радиус, {thl,th2} — граничные значения полярного угла. Чтобы нарисовать окружность, достаточно вызвать прими- , тив Circlet {х, у}, г]. Ниже представлено произведение искусства, состоящее исключительно из окружностей.

Чтобы было легче разобраться в этом шедевре, скажу, что он состоит из п = 8 семейств малых окружностей, вокруг которых имеется два "обода". Внешний (тонкий) обод — окружность. Внутренний (толстый) обод — семейство концентрических окружностей. Эти два обода как бы служат рамкой для шедевра. Сам шедевр состоит из п = 8 семейств маленьких окружностей, центры которых также лежат на окружности. Теперь, чтобы разобраться в шедевре, достаточно знать значения следующих величин, использованных при его построении:

n = 8 — количество семейств маленьких окружностей;

m= 40 — количество маленьких окружностей в каждом семействе;

r= 10 — радиус маленьких окружностей;

R = lr — расстояние от начала координат до наиболее удаленного (от начала координат) конца проведенного через начало координат диаметра окружности, на которой расположены центры маленьких окружностей; в программе положено i = 3;

i — номер семейства окружностей; отсчет номера начинается с 0;

j — номер маленькой окружности в семействе; отсчет номера начинается с 0;

Rtheta[t] — вектор с координатами {Cos[t], Sin[t]};

i*2*Pi/n — угол между осью абсцисс и отрезком, соединяющим начало координат с центром окружности, на которой расположены центры маленьких окружностей i-го семейства;

R*Rtheta[i*2*Pi/n] — координаты наиболее удаленного (от начала координат) конца проведенного через начало координат диаметра окружности, на которой расположены центры маленьких окружностей i-го семейства;

kr— расстояние от начала координат до ближайшего (к началу координат) конца проведенного через начало координат диаметра окружности, на которой расположены центры маленьких окружностей; в программе положено k = 1;

 k*r*Rtheta[i*2*Pi/n] — координаты ближайшего (к началу координат) конца проведенного через начало координат диаметра окружности, на которой расположены центры маленьких окружностей i-го семейства;

R1 = (R+k*r)/2 — радиус окружности, на которой находятся центры тех окружностей, на которых расположены центры маленьких окружностей семейств;

Rl*Rtheta[i*2*Pi/n] = (R+k*r)*Rtheta[i*2*Pi/n]/2 — координаты середины проведенного через начало координат диаметра окружности, на которой расположены центры маленьких окружностей /-го семейства; иными словами, это центр той окружности, на которой лежат центры окружностей i-го семейства;

rl = (R-k*r) /2 — радиус окружности, на которой расположены центры маленьких окружностей семейства;

Rl*Rtheta[i*2*Pi/n]+rl*Rtheta [i*2*Pi/n+j/m*Pi] — координаты центра у окружности i-го семейства.

Здесь умышленно сохранено большое количество параметров, так как это облегчает подбор нужного рисунка. Ниже изменены только два параметра.

На представленном ниже рисунке немного смещен центр окружностей семейства.

На представленной ниже вариации на эту же тему радиус окружности семейства переменный.

Пример 9.1. Колесо со спицами. Примитивов Circle и Line вполне достаточно для изобретения, простите, изображения колеса.

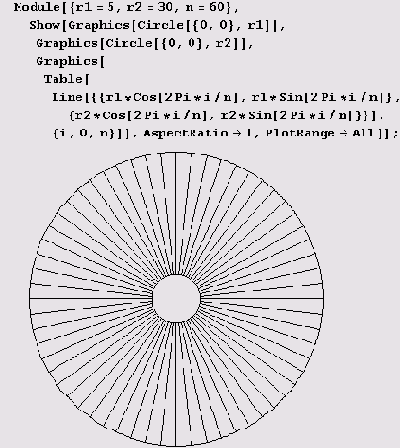
Но не перепутайте синус и косинус, а то получится колесо Эшера.

Эллипс и его дуга — примитив Circle

Дугу эллипса с полуосями rх и rу создает графический примитив circle [ {х, у], (rх, rу}]- Здесь {х, у] — координаты центра эллипса. Графический примитив Circle[{х, у], {rх, rу}, {thl, th2}] рисует дугу эллипса, которая получается из соответствующей дуги окружности. Центр эллипса находится в точке с координатами [х, у], rх и rу — полуоси, a (thl, th2] — граничные значения полярного угла для дуги окружности. Чтобы нарисовать эллипс, достаточно вызвать примитив circle ({x, у], (rх, rу}]. Ниже нарисован эллипс, окружность, диаметр которой совпадает с меньшей осью эллипса, и дуга окружности.

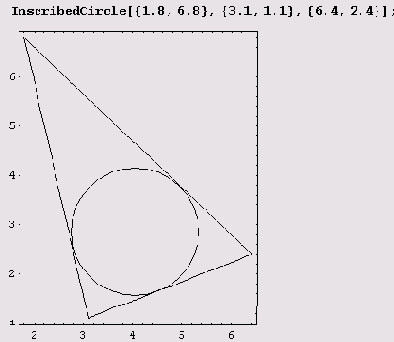
Пример 9.2. Окружность, вписанная в треугольник. Давайте напишем функцию inscribedcircle, которая по заданному своими вершинами треугольнику вписывает в него окружность. Предварительно нам понадобится функция, назовем ее inscribedCircleData, которая вычисляет радиус и координаты центра окружности, вписанной в треугольник.

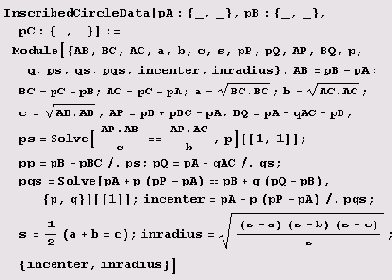
Теперь можем написать функцию, отображающую стороны треугольника и вписанную в него окружность.

(Здесь Sequence превращает Sequence@@InscribedCircleData[pA,pB,pC] в Sequence [рА,рВ,рС].)  Теперь можем приступить к рисованию.

Диски (закрашенные эллипсы, окружности и их сектора) — примитив Disk

Закрашенный диск получается с помощью примитива Disk, параметры которого в точности совпадают с параметрами примитива Circle. В частности, закрашенный круг получается с помощью примитива Disk[[х, у), r].

Текст

С помощью графического примитива Text [expr, {х, у} ] задается текст.

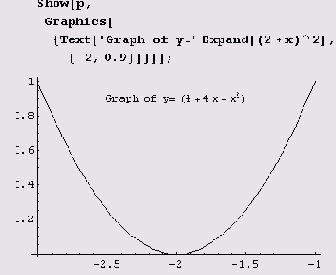
Здесь ехрr — любое выражение, причем центр печатной формы вычисленного его значения помещается в точку с координатами (х, у]. Предположим, мы нарисовали график параболы у = (2 + х) ^2 на отрезке [-3, -1] и обозначили через р графический объект р = Plot[ (2+х) ^2, {х,-3,-1}]. Тогда полученный нами рисунок можно снабдить поясняющим текстом.

В графическом примитиве Text можно задать еще один параметр — смешение offset Text [expr, coords, offset]. Этот параметр определяет смещение текста. По умолчанию он равен {0, 0}, а это означает, что центр текста должен находиться в точке с координатами coords. При установке {-1, 0} левый край текста начинается в точке с координатами coords; {l, 0} — правый край текста находится в точке с координатами coords; {0, -1} — текст центрируется выше точки с координатами coords; {0, 1} — текст центрируется ниже точки с координатами coords.

Вот пример использования смещения offset.

Наконец, параметр dir позволяет указать направление чтения текста: Text[ex/w, coords, offset, dir]. Если dir = {1,0}, то текст располагается как обычно, т.е. горизонтально. Если dir = {0, 1}, то текст размещается вертикально и читается снизу вверх. Если dir = {0,-!}, то текст располагается вертикально и читается сверху вниз. Если dir = (-1,0), то текст располагается горизонтально, но перевернутым, т.е. "вверх ногами".

Кроме того, добавить текст или другие графические примитивы в рисунки, созданные встроенными графическими функциями, можно с помощью опций Prolog и Epilog. По умолчанию они равны пустому списку {}. Однако в любой из этих списков можно добавить любые подходящие случаю примитивы. Разница между рассматриваемыми опциями состоит в том, что примитивы опции Prolog рисуются до основного рисунка, а примитивы опции Epilog — после.

В Приведенном ниже примере до рисования графика функции рисуется окружность.

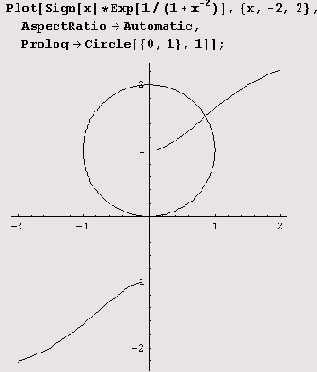
Ниже приведен пример использования опции Prolog вместе с вызовом в графическом примитиве Text функции FontForm, аргументами которой являются строка с текстом, название и размер шрифта для текста. На рисунке нарисовано два графика — график функции Эйри (решение дифференциального уравнения уn-ху = 0) и ее производной.


Вычерчивание графиков



Для вычерчивания графиков функций одной переменной имеется несколько функций. Самой важной из них является, пожалуй, Plot.

Функция Plot

Эта функция уже неоднократно встречалась нам ранее. Количество ее опций просто поражает.

Эта функция позволяет чертить сразу несколько графиков функций. Чтобы начертить сразу несколько графиков функций, в качестве первого аргумента функции Plot задается список функций. Для того чтобы различить графики, обычно используется опция PlotStyle -> {{dirl}, {dir2},...}, где dir1— совокупность графических директив, относящихся к 1-му графику, dir2— совокупность графических директив, относящихся к 2-му графику, и т.д. Ниже вычерчено два графика: парабола — жирной линией и прямая — потоньше. Кроме того, эти графики различаются цветом (на экране, конечно).

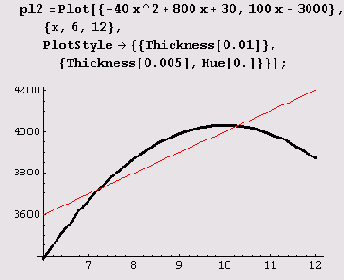
Заметьте, что координатные оси пересекаются на этом рисунке не в начале координат (не в точке с координатами (0, 0)). Однако если установить опцию AxesOrigin-> {xorigin, yorigin}, то оси будут пересекаться в точке с координатами (xorigin, yorigiri).

Рассмотрим пример построения графиков нескольких функций. Пусть функции, графики которых мы хотим построить, получаются с помощью функции Table или NDSolve. Для определенности пусть это будут полиномы Чебышева. Следующая строка ошибочна.

Plot[Table[ChebyshevT[n,x] ,{n,l,4}],{x,-l,l})

Дело в том, что здесь система Mathematica не сможет вычислить функции. Почему? Давайте разберемся. Начнем сначала. Вот график, который строится без проблем.

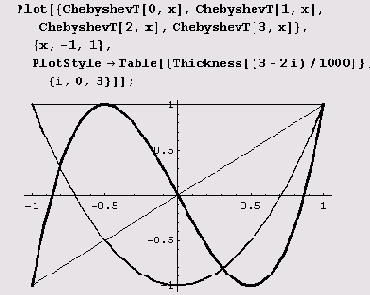
Здесь построены графики первых четырех полиномов Чебышева первого рода: ChebyshevT[0, x] — полином нулевого порядка, равный тождественно единице, ChebyshevT[l,x] = х, а также полиномы ChebyshevT[2,z] и ChebyshevT[3,x]. Но вот так график построить не удастся. 

list01={ChebyshevT[0,x],ChebyshevT[1,х],ChebyshevT[2,х],ChebyshevT[3,x]}

{1, х, -1 + 2х2, -Зх + 4х3} Plottlist0l,{х,-1,1}];

Plot::plnr: list0l is not a

machine-size real number at x =-1.. More...

Оказывается, система Mathematica не может вычислить значения list01! Почему? Потому что функция Plot имеет атрибут HoldAll.

Attributes[Plot] {HoldAll,Protected)

Этот атрибут указывает, что аргументы функций вычисляться не должны. Обычно аргументы функций вычисляются.

hh[1+2,2+3,3+4] hh[3,5,7]

Но если функции приписать атрибут HoldAll, вычисления аргументов выполняться не будут.

SetAttributes[hh,HoldAll] hh[l+2,2+3,3+4] hh[l+2,2+3,3+4]

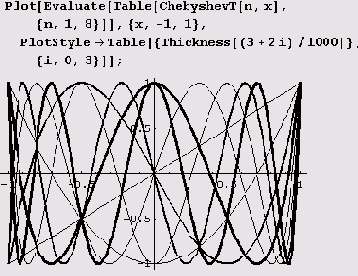
Чтобы в таких случаях выполнить вычисления, можно использовать функцию Evaluate. Выражение Plot [Evaluate [list0l], {x,-l, 1} ]; строит предыдущий график без проблем. Ниже построены графики 8 полиномов Чебышева.

Иногда на рисунке через точки координатных осей с координатными отметками нужно провести сетку вертикальных и горизонтальных прямых. Для этого достаточно установить опцию GridLines равной Automatic.

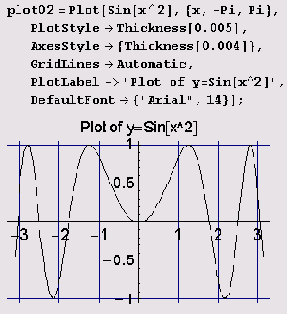
В данном случае сетка видна на графике функции у = sin x2, приведенном выше.

Опция PlotStyle задается так же, как и опции AxesStyle и FrameStyle, но определяет графический стиль линий.

При построении графиков система Mathematica использует адаптивный алгоритм, который предусматривает получение достаточно гладких кривых. Одним из критериев гладкости является величина угла между последовательными отрезками, аппроксимирующими график функции между соседними точками, в которых вычисляются ее значения. Величина этого угла устанавливается опцией MaxBend, по умолчанию он равен 10°. Вот график функции у = e-f .

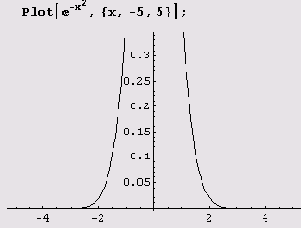
Как видите, график построен не полностью. Причина заключается в том, что вверху мы имеем слишком острый пик. Но если увеличить опцию MaxBend, например, до 15, пик будет нарисован полностью.

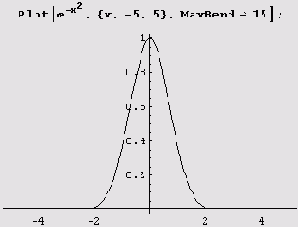
Иногда значение этой опции приходится уменьшать.

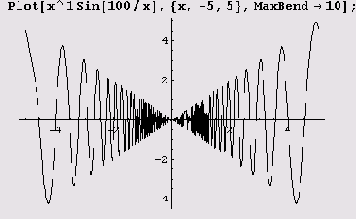
Слева хорошо заметен излом. Этот недостаток легко исправить.

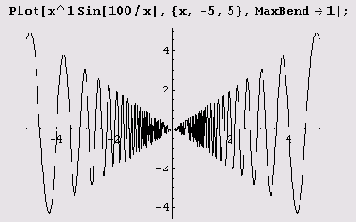
Как видите, несколько изъянов исчезло.

Количество точек, в которых производятся вычисления, регулируется опцией PlotPoints, которая по умолчанию равна 25. Если угол между последовательными сегментами превосходит значение опции MaxBend, то производится дробление интерзала между соседними точками, но таких шагов дробления не может быть больше, чем значение опции PlotDivision. Если это значение мало, график получится угловатым.

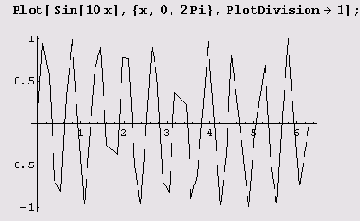
Если же использовать значение по умолчанию (оно больше 1), график будет более гладким.

Для уменьшения времени вычисления функций в выбранных по адаптивному алгоритму точках производится их компилирование, заключающееся в создании некоторого псевдокода. Однако это может привести к уменьшению точности вычислений. Чтобы избежать подобной потери точности, нужно применить опцию Compiled->False. Давайте посмотрим, для каких функций по умолчанию установлена опция Compiled->True. 
Block[{$Messages={}}, Select[Names["*"],

Options[ToExpression[I],Compiled]=={Compiled->True}&]]

 {ContourPlot,DensityPlot,FindMaximum,FindMinimum,FindRoot,

NDSolve,NIntegrate,NProduct,NSum,ParametricPlot,

 ParametricPlot3D,Play,Plot,Plot3D}

Построение графиков функций, заданных параметрически, — функция ParametricPlot

Функция ParametricPlot позволяет рисовать кривые и семейства кривых, заданных параметрически. Эта функция имеет те же опции, что и функция Plot. В некотором смысле эта функция универсальна. Если не учитывать неявно заданных функций, то именно функция ParametricPlot позволяет построить графики всех мыслимых функций, включая и многозначные. Без проблем строятся и графики, заданные в полярной системе координат. Фигуры Лиссажу, кривые Уатта, овалы Кассини, Декарта, Мюнгера, улитки Паскаля, однолистники, листы Декарта, всевозможные розы и розетки, рулеты, годографы, эволюты и эвольвенты всех мыслимых и немыслимых кривых, циклоиды, всевозможные спирали, циссоиды, конхоиды, строфоиды, астроиды, кардиоиды, неоиды, лемнискаты, узлы, квадратрисы, клотоиды, кохлеоиды, трохоиды, элипсиды, катакаустики, всевозможные параболы, локсодромы и лоциклики, трезубцы, трисектрисы, трилистники, верзиеры, брахистохроны, подэры, кривые с именами древнегреческих и средневековых ученых — вот далеко не полный перечень всевозможного зверья, которое может быть нарисовано функцией ParametricPlot.

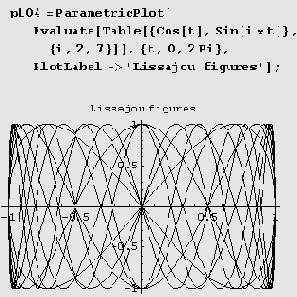
Пример 9.3. Фигуры Лиссажу. Это классический пример применения функции ParametricPlot. Рисуются эти фигуры совсем просто, и потому мы нарисуем сразу несколько.

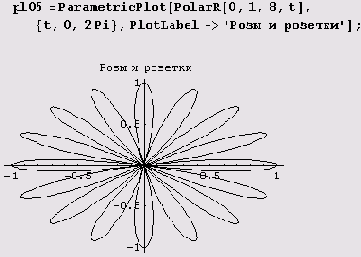
Пример 9.4. Розы и розетки. Эти цветы весьма многочисленны, выглядят, как правило, очень мило и легко рисуются. Процесс вычерчивания совсем прост, если предварительно определить следующую функцию. 
PolarR[al,a2_,omega_,phi_]:=Module[{r=al+a2*Cos[omega*phi]},

<r*Coi[phi],r*Sin[phi]}]

Вот как, например, с помощью этой функции рисуется многолепестковая роза.

А вот еще один милый цветок.

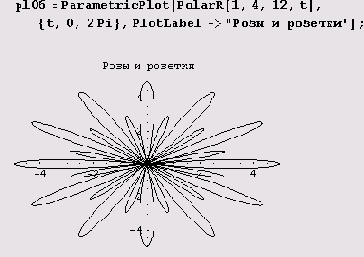
Цветы эти столь разнообразны, что согласия относительно количества их видов нет. Одни насчитывают более полтора десятка видов, другие — не менее сотни.

Пример 9.5. Кривые в полярных координатах. Построение кривых в полярных координатах значительно упрощается, если предварительно определить функцию PolarXY.

PolarXY[r_,phi_]:=

{r*Cos[phi],r*Sin[phi]}

Вот как, например, с помощью этой функции рисуется улитка Паскаля.

Пример 9.6. Полярные зверинцы. Иногда приходится подбирать параметры в семействе кривых, заданных в полярных координатах. Этот процесс значительно упрощается, если предварительно в определение функции PolarXY ввести параметры, которые определяют кривую семейства.

PolarXYAB[r_,phi_, а_,b_]:=

{r*Cos[a*phi],r*Sin[b*phi]}

Вот как, например, с помощью этой функции рисуется одна из кривых семейства.

Как вам эта зверушка? Понравилась? Если да, вы подобрали параметры! Если нет, пробуйте другие параметры.

Ну а эта зверушка? Неужели не нравится? Тогда продолжайте перебирать параметры...

Пример 9.7. Годографы. Иногда приходится вычерчивать годографы семейства вектор-функций, заданных в полярных координатах. В определении такой функции часто участвует некий вектор (очень часто единичный), который с течением времени вращается вокруг начала координат. Пусть, например, нужно вычертить годограф вектор-функции r(t) = аte + Rt+a(e) + АRwt+p(e), где e — единичный вектор, Rф — поворот на угол ф вокруг начала координат, а а, а, А, w, p — заданные параметры. Тогда, чтобы упростить определение функции PolarXYAB, можно поступить так. Сначала определим следующую функцию.

Rphi[phi_]:={Cos[phi],Sin[phi]}

С ее помощью значительно упрощается определение функции PolarXYAB, которое упрощает задание кривой семейства.

PolarXYAB[t_,a_,alpha_,aa_,omega_,beta_]:=

{0,a*t}+Rphi[t+alpha]+aa*Rphi[omega*t+beta]

Вот как, например, с помощью этой функции рисуется одна из кривых семейства.

Как вам эта зверушка? Если думаете, что они все такие, вы ошибаетесь.

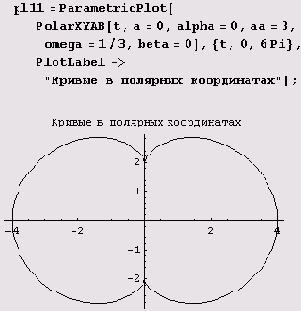
Вращающийся единичный вектор очень часто полезен и при вычерчивании других кривых, например циклоид.

Пример 9.8. Циклоиды. Циклоиды (высших порядков) описываются уравнением Z = l0+l1tiwt+l2tiwt+..+lntiwn. Вот как, например, выглядит определение функции PolarXYAB для циклоид некоторого определенного типа.

PolarXYAB[t ,rl_,r2_,a_,omega_]:=

r1+r2*Rphi[t]+a*Rphi[omega*t]

Вот как теперь рисуется одна из циклоид.

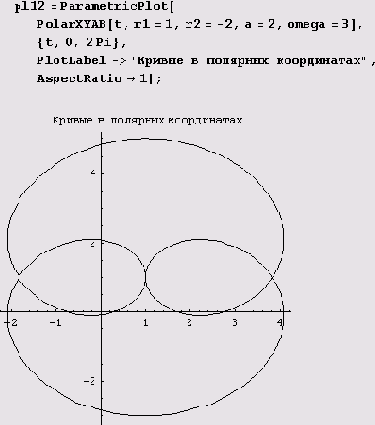
Пример 9.9. Гиперболы в полярных координатах. Введенную нами функцию

PolarXY[r_, phi_] : = { r*Cos [phi], r*sin [phi]} удобно использовать также в определении функции PolarXYAB для многих функций, заданных в полярных координатах. Посмотрим, как это делается на примере вычерчивания полярных гипербол.

Вы знаете, как выглядит полярная гипербола 

Если нет, вас ждет сюрприз!

Сначала дадим определение функции PolarXYAB для полярных гипербол.

PolarXYAB[t_,a_,b_]:= PolarXY[r=a+ b/t,t]

Вот как теперь рисуется полярная гипербола.

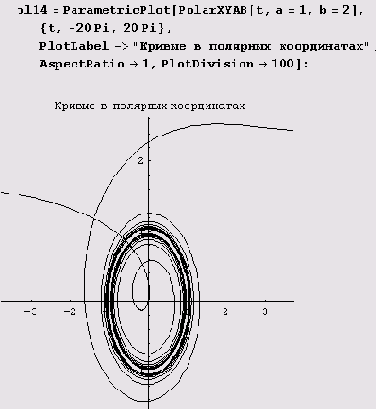
Позвольте вас спросить, а сколько асимптот у полярной гиперболы?!

Пример 9.10. Параболы в полярных координатах. Применим теперь введенную нами функцию PolarXY[r_, phi_] : = {r*Cos [phi], r*sin[phi] } для вычерчивания полярных парабол r= аφ2+bφ+с. Сначала дадим определение функции PolarXYAB для полярных парабол.

PolarXYAB[t_,а_,n ,с_]:=

PolarXY[r=a*t~2+b*t+c,t]

Вот как теперь рисуется полярная парабола.

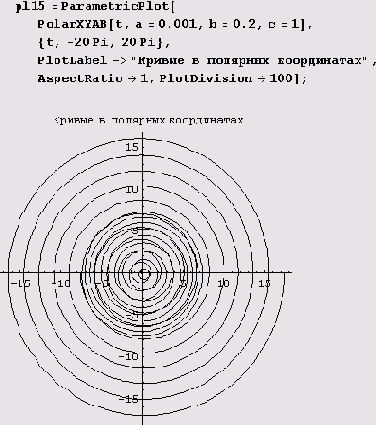
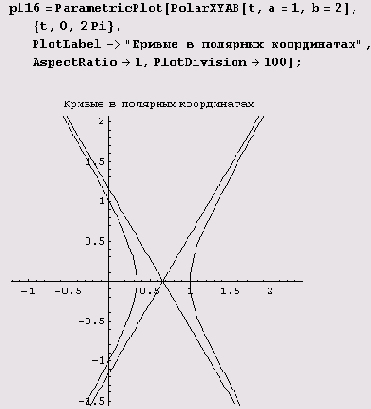
Пример 9.11. Кривые второго порядка в полярных координатах. Ну а сложно ли вычертить в полярных координатах обычную кривую второго порядка? Нисколько. Сначала дадим определение функции PolarXYAB для обычных кривых второго порядка.

PolarXYAB[t_,a_,b_]:=

Pol^rXY[r=l/(a+b*Cos[t]) , t]

В зависимости от параметров у нас получится обычная кривая второго порядка, причем фокус будет находиться в начале координат. Вот как рисуется обычная гипербола.

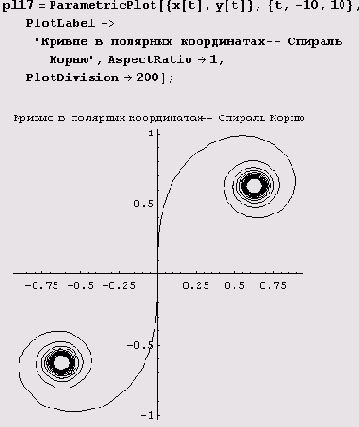
Пример 9.12. Спираль Корню. Предположим, нужно начертить кривую, которая имеет сложные параметрические уравнения х = x(i) и у = y(t). Тогда лучше всего предварительно определить функции х = x(t) и у - y(t) и именно их использовать в функции ParametricPlot. Покажем, как это делается на примере спирали Корню. В соответствии с рекомендацией сначала определяем x(f) и y(f) для спирали Корню.

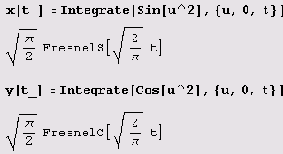
Как видите, система Mathematica заметила, что x(t) и y(f) являются интегралами Френеля. Теперь, определив x(t) и y(t), можем построить график.

Специальные типы графиков

Как мы видели, функция ParametricPlot практически универсальна. Однако часто приходится строить графики специального вида. Тогда можно воспользоваться более специализированными функциями.

Графики в полярной системе координат

Построение графиков в полярной системе координат зачастую упрощается, если воспользоваться функцией PolarPlot из пакета Graphics`Graphics`. Пакет этот загружается как обычно. <<Graphics` Graphics`

Ниже показано, как нарисовать эллипс и улитку на одном графике.

Пример 9.13. Несколько графиков в разных системах координат на одном чертеже.

Иногда на одном листе (чертеже) нужно начертить несколько графиков, притом в разных системах координат. Предположим, на одном листе нужно начертить четыре графика, расположив их в два ряда по два графика, т.е. два графика в верхнем ряду и два — в нижнем. Два графика создадим с помощью функции ParametricPlot, a два — с помощью функции PolarPlot. Сначала загружаем нужный графический пакет.

<<Graphics `Graphics`

А теперь задаем радиус-вектор как функцию угла

Сlearг[r]

г[theta_]=Sin[8 theta/7];

и определяем первый график.

ppl=ParametricPlot[{г[theta]Cos[theta],r[theta]Sin[theta]},

{theta,0,14Pi},AspectRatio->Automatic,DisplayFunction->Identity] ;

После этого точно так же готовим второй график. 
Clear[r]

r[theta_]=theta*Cos[ theta];

pp2=ParametricPlot[{r[theta]Cos[theta],r[theta]Sin[theta]},

{theta,-19Pi/2,19Pi/2},AspectRatio->Automatic,PlotPoints->200,

DisplayFunction->Identity];

Аналогично строим третий график, но в полярных координатах с помощью функции PolarPlot. 
Clear[r]

r[theta_]=Exp[Cos[ theta]]-2Cos[4theta]+Sin[theta/12]Л5;

pp3=PolarPlot[r[theta],{theta,0,24Pi},AspectRatio->Automatic,

PlotPoints->200,PlotRange->{{-4,5},{-4.5,4.5}},

DisplayFunction->Identity];

Последний, четвертый, график тоже строим в полярных координатах с помощью функции PolarPlot. 
Cleart[r]

pp4=PolarPlot[{Sqrt[l/theta],-Sqrt[I/theta]},{theta,0.1,lOPi},

AspectRatio->Automatic,PlotPoints~>200,

PlotRange->All,DisplayFunction->Identity] ;

Наконец, группируем четыре графика в двухмерный массив с помощью функции GraphicsArray и отображаем все четыре графика (полученный массив из двух строк по два графика в строке) с помощью функции show.

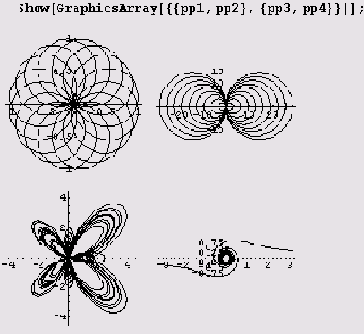
Как видите, все очень просто! Зато сейчас вам предстоит ответить на очень трудный вопрос: какая из функций PolarPlot и ParametricPlot лучше подходит для создания графика функции, заданной в полярных координатах? По собственному опыту могу сказать, что часто ответ очевиден, но иногда легче начертить по сотне графиков с помощью обеих функций, чем обосновать без ссылок на личные предпочтения выбор конкретной функции!

График функции, заданной на дискретном множестве точек, — функция ListPlot

Функция ListPlot предназначена для построения графика функции, заданной на дискретном множестве точек. Поэтому ее первый аргумент является либо списком значений функции (в этом случае считается, что эти значения функция принимает в точках 1, 2, 3, ...), либо списком пар вида [абсцисса, ордината]. Конечно, этот список можно создать и какой-либо функцией, например Table. У этой функции есть одна отличительная особенность: размером точек управляет графическая директива Pointsize, а не Thickness, потому что в данном случае мы имеем точки, а не линии. Впрочем, иногда точки на графике нужно соединить отрезками прямых. Для этого в функции ListPlot нужно установить дополнительную опцию PlotJoined->True. К другим часто используемым опциям относятся AxesOrigin, GridLines и PlotStyle.

Плоские графики функций двух переменных

Казалось бы, плоскость двухмерна, и потому на ней можно рисовать графики только одной переменной. Но, оказывается, что на самом деле, хотя плоскость и плоская, ее можно раскрасить и с помощью цвета отобразить значение функции от двух независимых переменных! До этого давно додумались картографы. Система Mathematica тоже умеет использовать эту возможность. Функции ContourPlot и DensityPlot позволяют графически изображать функции двух независимых переменных. Функция ContourPlot, например, строит линии уровня. Первым аргументом рассматриваемых

функций является выражение, задающее функцию двух переменных. Независимые переменные и области их изменения определяются с помощью двух списков вида [переменная, минимальное_значение, максимальное_значение], следующих за первым аргументом.

Линии уровня

Вы наверняка видели топографические карты какой-нибудь местности и физические карты материков, океанов и островов. И, несомненно, вы не могли не заметить на них линии уровня. Вдоль таких линий высота над уровнем моря постоянна. Если двигаться по таким линиям, высота над уровнем моря не будет изменяться. Но высоту над уровнем моря можно рассматривать как функцию точки. Линии (точнее, множества) точек, на которых функция постоянна, называются линиями уровня, или изолиниями (данной функции). В системе Mathematica есть две функции, предназначенные для вычерчивания графиков с линиями уровня: ContourPlot и ListContourPlot.

Функция ContourPlot

Эта функция вычерчивает графики функций, заданных аналитически. Вот как, например, можно вычертить график функции z — sin xy с линиями уровня.

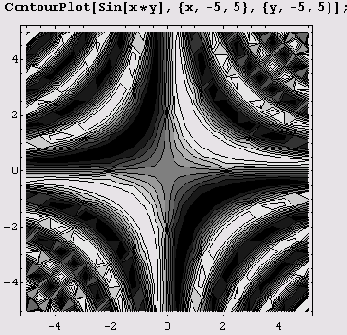
Как видите, это подобно раскраске физической карты. Иногда нужно оставить только линии уровня, а сам график не раскрашивать. Тогда нужно воспользоваться опцией ContourShading->False.

Иногда, наоборот, нужно оставить только раскраску, а изолинии сделать невидимыми. Тогда нужно воспользоваться опцией ContourLines->False.

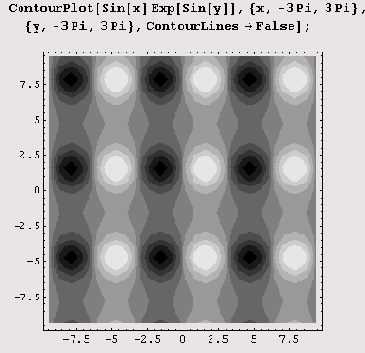
Контурный график можно раскрасить. Для этого нужно воспользоваться опцией ColorFunction->Hue. (По умолчанию установлено ColorFunction->Automatic, что приводит к раскраске оттенками серого.) В случае опции ColorFunction->Automatic области с меньшими значениями функции имеют более темные оттенки серого цвета, чем области с большими значениями функции. Иногда нужно подобрать цвета. Тогда придется поэкспериментировать с этой опцией. Можно, например, установить ColorFunction->(Hue[l-t]&), ColorFunction->(Hue[Abs[0.5-i]]&) или ColorFunction-> (Hue [1-Sin [Pi (l-#) ] ] &). По возможности можете руководствоваться правилами цветового дизайна, я же советов давать не буду, поскольку, как известно, на вкус и на цвет товарища нет...

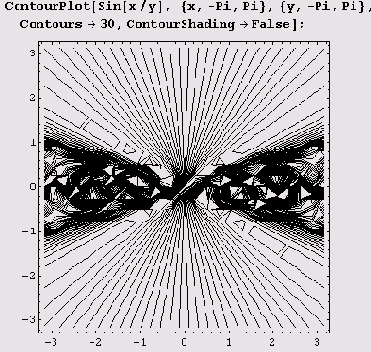
Как быть, если нужно отображать только изолинии, соответствующие заранее заданному количеству уровней, или только изолинии заданных уровней? Нет проблем! Для этого есть опция Contours. По умолчанию число линий уровня на рисунке равно десяти, но если установить Contours->1 то будут отображаться только изолинии и уровней, равномерно распределенных между максимальным и минимальным значениями функции. На следующем графике отображаются только изолинии 30 уровней.

Если же нужно отображать только изолинии заданных уровней, то опцию Contours нужно установить равной списку этих уровней.

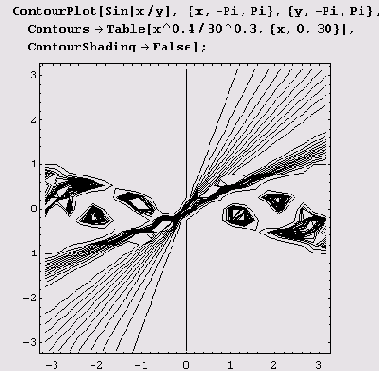
Список стилей контурных линий можно задать в опции ContourStyle. Например, если установить ContourStyle->{{RGBColor[1,0,0]},{RGBColor[0,0,l]}}, то будет чередоваться красный и синий цвета контурных линий.

По умолчанию значение опции PlotPoints равно 25. При увеличении этого значения на графике могут появиться дополнительные детали. Вот как изменится предыдущий график, если его установить равным 50.

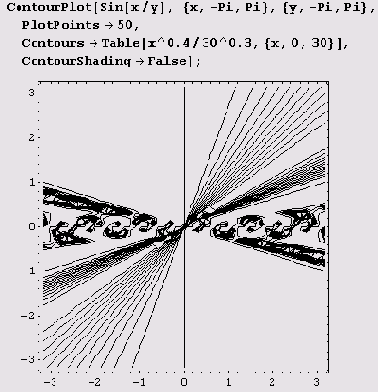
Кроме перечисленных, функция ContourPlot имеет также опции AxesOrigin, Compiled и ContourSmoothing.

При установке ContourSmoothing->True происходит сглаживание линий уровня.

Функция ListContourPlot

Эта функция вычерчивает фафики функций, заданных таблично. В приведенном ниже примере таблица значений функции сгенерирована с помощью функции Table.

Фактически в таблицу заносятся значения функции cos(sin(;c2 + ;y2)), к которым добавляется случайное возмущение с помощью функции Random [Real, {-0.2,0.2}].

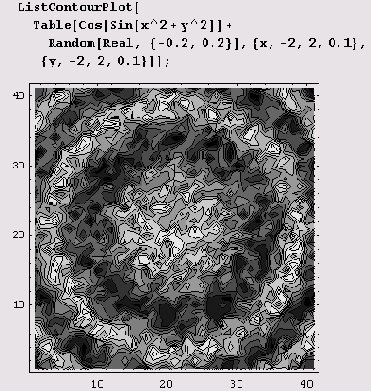
Графики плотности

Для построения графиков плотности в системе Mathematica имеются функции DensityPlot и ListDensityPlot.

Функция DensityPlot

Эта функция отображает значения исследуемой функции в ячейках регулярной сетки с помощью окрашивания этих ячеек либо в серый цвет, либо в цвета палитры, задаваемой функцией Hue. Ниже приведен пример такого графика с окраской в серые тона.

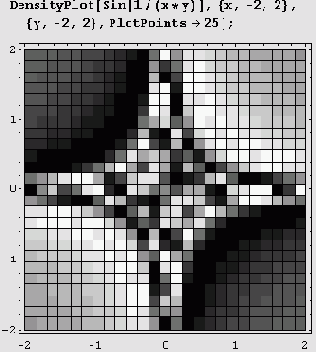
При увеличении значения опции PlotPoints количество деталей, естественно, возрастает.

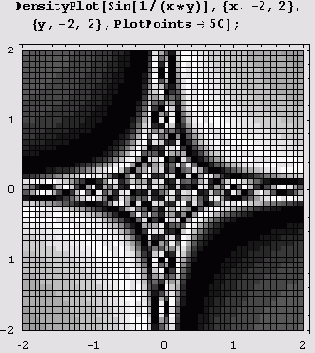
Если хотите убрать разграфку на ячейки (сетку), установите Mesh->False.

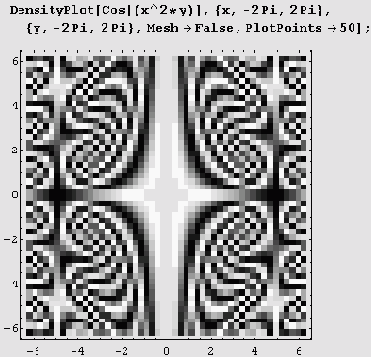
Стиль ячейки определяет опция MeshStyle. В этой опции можно использовать Dashing, Thickness, GrayLevel, Hue И RGBColor.

Дополнительно у функции DensityPlot есть опции ColorFunction и Compiled.

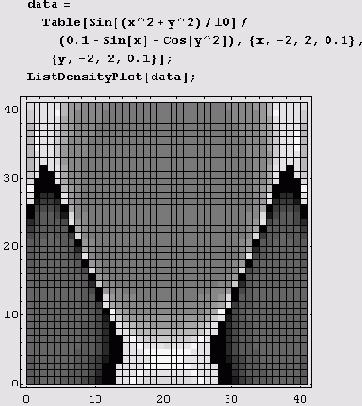
Функция ListDensityPlot

С помощью этой функции строится график плотности таблично заданной функции. В приведенном ниже примере сначала генерируется таблица, а затем применяется функция ListDensityPlot для построения графика плотности по табличным данным.

Конечно, по умолчанию отображается сетка.

Специальные виды графиков

К специальным видам графиков относятся диаграммы, графики с текстовыми данными и огромное множество других видов.

Диаграммы и гистограммы

Этот вид графиков в системе Mathematica весьма многочисленный. Ни численностью, ни возможностями оформления этого вида графиков система Mathematica не уступает самым лучшим специализированным пакетам. Рассказывать обо всем этом богатстве с помощью черно-белых рисунков — значит отвергать пословицу: лучше один раз увидеть, чем сто раз услышать. Поэтому я не стану утомительно перечислять всевозможные опции и приводить серенькие рисунки. Если есть потребность, вызовите справочную систему И найдите описание функций BarChart, GeneralizedBarChart, StackedBarChart, PercentileBarChart, PieChart, Histogram и их многочисленных опций, призванных удовлетворить самые изысканные вкусы. Впрочем, мне кажется, что все диаграммы наиболее эффектно смотрятся лишь в цвете.

Графики с текстом

Что бы вы сказали о картине, на которой художник с помощью текста подписал бы все детали. Ну, например, чтобы вы сказали о Джоконде, если бы она пестрела надписями вроде "левая рука", "правая рука", "левый мизинец", "правый мизинец", "портьера", "штора", "левый глаз", "правый глаз", "улыбка" и т.д. Думаю, Джоконда потеряла бы свой шарм. Но бывают случаи, когда надписи просто необходимы. На географических картах, например. Вы знаете, как их сделать. Но, оказывается, есть специальные функции, которые для изображения точки используют не маленький кружочек, а цифры или даже любое выражение системы Mathematica! При этом вы можете отображать точку или только надпись.

Функции TextListPlot и LabeledListPlot

Функции TextListPlot и LabeledListPlot можно вызвать тремя способами.

1-й способ. TextListPlot [ у1 , у2, ...} и LabeledListPlot [ y1 , у2, ...]. При этом способе точка с координатами (/', у,) помечается с помощью числа /. Если используете TextListPlot, то даже точки не увидите — только число. Вот первые 25 десятичных знаков основания натуральных логарифмов.

data=First[RealDigits[N[E,25]]]

{2,7,1,8,2,8,1,8,2,8,4,5,9,0,4,5,2,3,5,3,6,0,2,8,7}

А вот как полученные данные можно отобразить на графике.

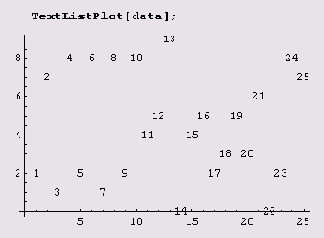
Точки графика просто изображаются их номерами. А вот функция LabeledListPlot отображает точки и перенумеровывает их.

2-й способ. TextListPlot [ {x1, у1 }, { х2, у2}, ...] и LabeledListPlot [ { х1, у1 }, { х2, у2}, ...]. При этом способе точка с координатами (*,, yt) помечается с помощью числа .

3-й способ. TextListPlot [{ х1, у1, выражение^, {х2, у2, выражениег}, ...] и LabeledListPlot [{ х}, у1 , выражение^ , { х1, у2, выражение?.}, ...]. При этом способе точка с координатами (х1, y1) помечается с помощью выражение,.

Пусть, например, имеем следующее.

А вам написать Спираль по спирали слабо?

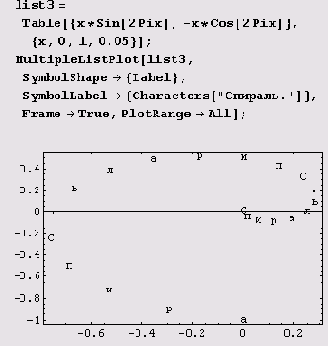
Функция MultipleListPlot

Честно говоря, строку "Колебаться, колебаться, колебаться завещал нам Великий Синус... " записывать по синусоиде с помощью функции LabeledListPlot несколько хлопотно, так как нужно написать выражение, выбирающее нужный символ из списка. В пакете <<Graphics`MultipleListPlot` функция MultipleListPlot делает это автоматически. Вообще-то, эта функция предназначена для создания графиков нескольких табличных функций и потому вызывается так: MultipleListPlot [сиисок,, список^, ...]. Вот синус и косинус, заданные таблично, на одном графике.

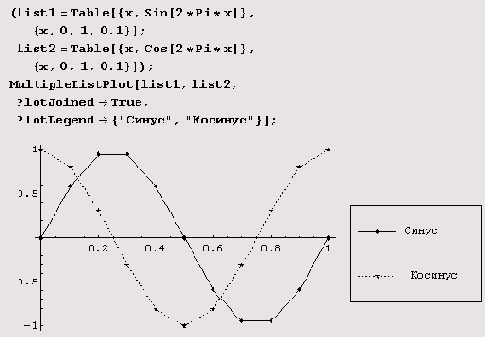
Количество опций этой функции просто поражает. Опция SymbolLabel позволяет указывать последовательность символов, которые используются для пометки точек графика.

Пусть имеем следующее.

list3=Table[{x*Sin[2 Pi x],-x*Cos[2 Pi x] }, {x,0,1,0.05 } ];

Тогда получим вот это.

Построение графиков неявно заданных функций — функция ImplicitPlot пакета Graphics`ImplicitPlot`

Труднее всего, пожалуй, рисовать графики неявно заданных функций. Для вычерчивания графиков таких функций в системе Mathematica предусмотрен пакет Graphics`ImplicitPlot`, который загружается обычным образом: <<Graphics`ImplicitPlot`. В нем для построения графиков неявно заданных функций имеется функция ImplicitPlot. Ее первым параметром всегда является уравнение, определяющее неявно заданную функцию. Функция одной переменной задается неявно с помощью уравнения. Вид этого уравнения может быть любым допустимым в системе Mathematica; совсем не обязательно его приводить к виду F(x, у) = 0. Уравнение в системе Mathematica имеет вид левая часть == правая часть. Обратите внимание на двойной знак равенства, соединяющий левую и правую части. Уравнение нельзя записать с одним знаком равенства, т.е. в виде левая часть = правая часть, поскольку это присваивание. Функция ImplicitPlot пакета Graphics`ImplicitPlot` используется для построения графиков неявно заданных функций одной и двух переменных.

Построение графика неявно заданной функции одной переменной

При построении графика неявно заданной функции одной переменной применяются два метода:

 решение уравнения; нужно задать интервал изменения переменной;  нахождение линии уровня; задаются интервалы изменения обеих переменных.


Построение графика неявно заданной функции одной переменной при изменении переменной на заданном интервале методом решения уравнения

При построении графика неявно заданной функции одной переменной различаются два случая:

 построение графика неявно заданной функции одной переменной при изменении переменной на заданном интервале;  построение графика неявно заданной функции одной переменной при изменении переменной на заданном интервале, из которого исключено несколько точек.


Чтобы построить график решения уравнения, найденный функцией Solve на интервале изменения переменной (xmin, xmax), нужно вызвать функцию ImplicitPlot [уравнение, {переменная, xmin, xmax}].

Пример 9.14. "Кривая дьявола". Эта кривая задается уравнением dс4 -9cn:2 = уn -100y2. С помощью функцииImplicitPlot рисуется она совсем просто.

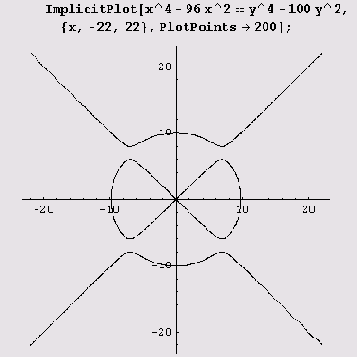
Пример 9.15. Кривая х4 + у4 = х2 + у2. Эта кривая с помощью функции ImplicitPlot рисуется совсем просто, если заметить, что в полярных координатах она задается  уравнением вида 



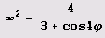
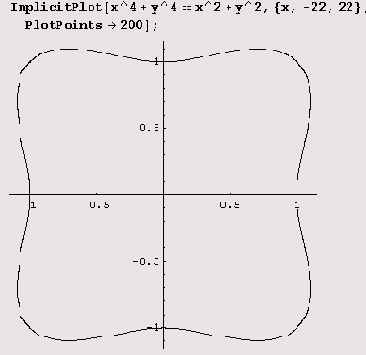
Заметьте, что хотя для х интервал изменения был взят с большим запасом, график увеличен за счет того, что функция ImplicitPlot сообразила, что отображать весь заданный интервал нет необходимости.

Пример 9.16. Кривая у5 + x4 = ху2. Эта кривая с помощью функции ImplicitPlot рисуется совсем просто, если заметить, что все интересные детали лежат в интервале (-10, 10).

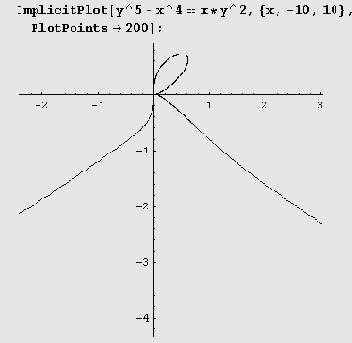
По поводу этого и других графиков неявно заданных функций нужно сделать следующее замечание. Система Mathematica вычерчивает графики очень аккуратно и весьма точно. Однако в случае неявно заданных функций свойства вычерчиваемых кривых далеко не всегда очевидны из уравнения. Аккуратное вычерчивание иногда также может скрывать эти свойства. Например, иногда очень трудно отличить криволинейную дугу от отрезка прямой, а из-за этого можно пропустить точку перегиба. В ГУ квадранте вычерченного системой Mathematica графика, например, есть точка перегиба. Однако на глаз заметить ее очень трудно, поскольку криволинейная дуга почти сливается с прямой. В учебных пособиях в таких случаях обычно жертвуют точностью и приводят эскиз графика, на котором характерные точки кривой легко заметны на глаз. Система Mathematica же точностью жертвовать не может, и потому иногда требуется дополнительное исследование графика, которое можно провести, конечно же, с помощью системы Mathematica.

В первом квадранте, например,

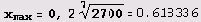
Пример 9.17. Кривая x5 + у5 = ху2. Эта кривая с помощью функции ImplicitPlot рисуется совсем просто, если заметить, что все интересные детали лежат в интервале (-1, 1).

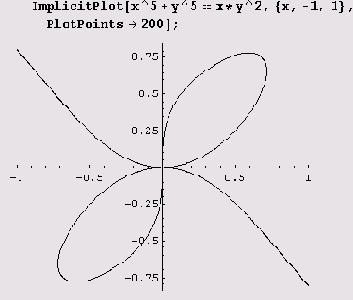
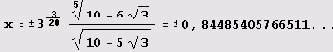
График опять вычерчен очень аккуратно и весьма точно. И опять очень трудно отличить криволинейную дугу от отрезка прямой, и из-за этого абсциссы    точек локальных экстремумов в I и III квадрантах, а также уравнения вертикальных касательных  2 с первого взгляда.

Трудные случаи построения графика неявно заданной функции одной переменной в заданном интервале изменения переменной с помощью функции ImplicitPlot. Построение графика неявно заданной функции одной переменной даже в заданном интервале изменения переменной — весьма непростая задача. Функция ImplicitPlot во многих случаях справляется с ней блестяще. Но далеко не во всех случаях. Вот тривиальный пример. 

ImplicitPlot[Min[x,у]==1,(х,-22,22},PlotPoints->200];

 Solve::dinv :

The expression Min'0'1* [x, y] involves unknowns in more than one argument,

 so inverse functions cannot be used. More...

ImplicitPlot::epfail: Equation Min[x,y]==l

could not be solved for points to plot.

Конечно, уравнение Min[x,y]= =1 определяет неявно заданную функцию, график которой представляет собой прямой угол с вершиной в точке (1; 1), причем стороны его параллельны осям координат. Потому с этим примером должен без труда справляться даже шестиклассник. Впрочем, функция ImplicitPlot с этим графиком тоже может справиться, но после некоторой подсказки.

Вот еще один трудный (для функции ImplicitPlot) случай.

С этим примером должен без труда справляться даже восьмиклассник. (Правда, если он хочет участвовать в районной (городской) олимпиаде или поступить на мехмат.) И вот еще один совсем "позорный" пример.

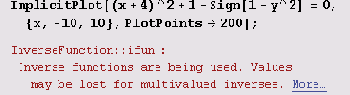
А вот этот простенький пример считается неоправданно долго.

Это поистине удивительно, потому что графики для всех сомножителей строятся очень быстро!

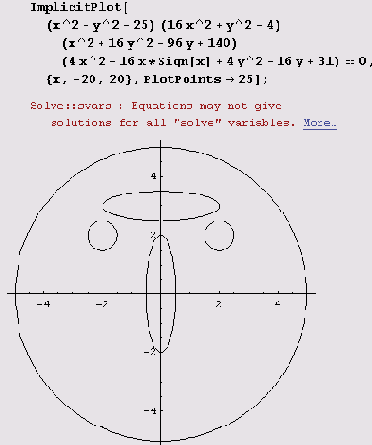
Предостережение. Заглянув в справочную систему, вы можете попытаться построить этот график так 
ImplicitPlot[x^2+y^2-25==0,16 х^2+у^2-4==0,

х^2+16у^2-96у+140==0,

4x^2-16x*Sign[х]+4у^2-16у+31==0,

{х,-20,20},

PlotPoints->25];

или так 
ImplicitPlot[x^2+y^2-25==0,16

х^2+у^2-4==0,

х^2+16у^2-96у+140==0,

4х^2-16х*Sign[х]+4у^2-16у+31==0,

{х,-20,20},{у,-20,20),

 PlotPoints->25];

Вы увидите, что ничего не произойдет! На самом деле вызов нужно записать вот так 
ImplicitPlot[{x^2+y^2-25==0,16

х^2+у^2-4= =0,

х^2+16у^2-96у+140==0,

4х^2-16х*Sign[х]+4у^2-16у+31==0},

{х,-20,20},

PlotPoints->25];

или так 
ImplicitPlot[{x^2+y^2-25==0,16

 x^2+у^2-4==0,

х^2+16у^2-96у+140==0,

4хл2-16х*Sign[х]+4у^2-16у+31==0},

{х,-20,20},{у,-20,20),

PlotPoints->25];

Фактически это построение графиков нескольких неявных функций. Мы этот случай рассмотрим чуть позднее.

Построение графика неявно заданной функции одной переменной при изменении переменной на заданном интервале, из которого исключено несколько точек.

Чтобы построить график решения уравнения, найденного функцией Solve на интервале изменения переменной (xmin, xmax) , из которого исключено несколько точек, нужно в вызове функции ImplicitPlot [уравнение, (переменная, xmin, xmax}] между xmin, и хmах через запятую перечислить все исключаемые точки. Впрочем, функция ImplicitPlot, как правило, сама избегает значений, которые доставляют хлопоты, и потому прибегать к этой форме вызова не приходится даже в следующих двух классических случаях.


 

Построение графика неявно заданной функции одной переменной при изменении переменных на заданных интервалах методом нахождения линии уровня

Уравнение F, (х, у) = F2 (х, у) можно записать в виде F, (х, у) - F, (х, у) = 0. Так что фактически вместо решения уравнения F, (х, у) = F2 (х, у) можно найти линию уровня функции F, (х, у) - F2 (х, у), на которой она равна 0. Как дать такую подсказку функции ImplicitPlot? Очень просто: нужно указать интервалы изменения обеих переменных. Рассмотрим примеры, когда это полезно.

Ранее с помощью вызова ImplicitPlot[Min[x,у] ==1, {x,-22,22},PlotPoints-> 200]; мы не смогли построить график неявной функции Min[x,y]==l. А вот с подсказкой ImplicitPlot[Min[x,y]==l,{х,-22,22},(у,-22,22},PlotPoints->200]; график строится мгновенно. Вызов

ImplicitPlot[ (х^2+у^2-25) (16 х^2+у^2-4)*

*(х^2+16у^2-96у+140)

 (4х^2-16х*Sign[х]+4у^2-16у+31)==0,

{х,-5,5}, (у,-5,5),

PlotPoints->25];
строит график более десяти минут, а вызов
 ImplicitPlot [(х^2+у-2-25) (16 х^2+у^2-4)

 (х^2+16у^2-96у+140)

 (4x^2-16x*Sign[х]+4у^2 -1бу+31)==0,

{х,-5,5}, {у,-5,5),

 plotPoints->250];

нужно менее трети секунды.

Вот еще один график, который без подсказки не строится вообще.

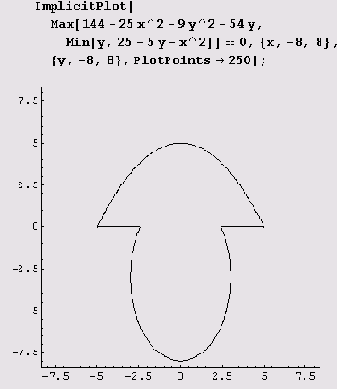
График

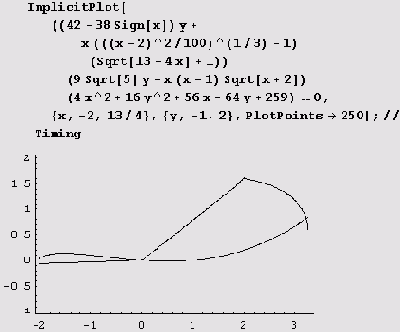
строится за 0,344 секунды. Важна ли тут подсказка (у,-1,2}? Оказывается, график можно построить и без нее, но это займет немалое время даже при PlotPoints->25.

Построение графиков нескольких неявных функций

Построение таких графиков теоретически сводится к построению графика одной неявной функции. Пусть нужно построить графики неявных функций, заданных уравнениями

F1(х, у) = Ф1(х, у), F2 (х, у) = Ф2(х, у), F3 (х, у) = Ф3(х, у), ..., Fn (x, у) = Фn(х, у).

Тогда мы можем привести эти уравнения к виду F1(х, у) - Ф1(х, у) = 0, F2 (х, у) - Ф2(х, у) = 0, F3 (х, у) - Ф3(х, у) = 0, ..., Fn (х, у) - Фn(х, у) = 0 и построить график (F1 (х, у) - Ф1(х, у))( F2(х, у) - Ф2(х, у))( F3 (х, у) - Ф3(х, у))...( Fn (х, у) - Фn(х, у)) = 0.

Но на практике лучше поступать не так, а совсем наоборот. Например, построение графика 
ImplicitPlotf

((42-38Sign[x])y+x^(х-2) ^2/100) ^ (1/3) -1)

 (Sqrt [13-4х]+1) )

 (9Sqrt[5]-x(x-l)Sqrt[x+2])(4х^2+16у^2+56х-64у+259)==0,

{х,-2,13/4),
PlotPoints->25];//Timing

можно заменить построением следующего графика.

График 
ImplicitPlot[((4у+х^2)^2+Sign[х^2+2х]+1)

((х^2+у^2)^(5/2)-4х(х^2-у^2))==0, {х,-5,5},
PlotPoints->25];//Timing

можно строить часами, а график

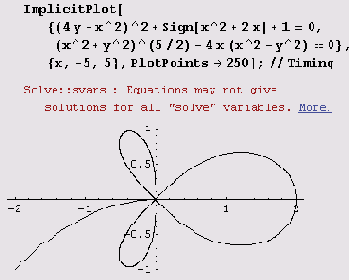
строится всего за 21,641 секунды. Этот график можно попытаться построить и как линию уровня.

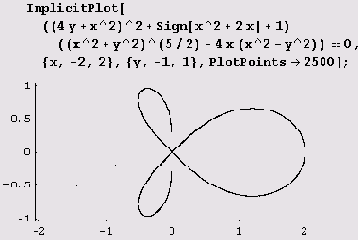
Этот способ потребует всего лишь 17,859 секунды. Но обратите внимание на отсутствие ножки у трилистника. Вместо нее на экране всего лишь несколько почти незаметных точек. Попытка же увеличения значений параметров PlotPoints и PlotDivision может привести к неоправданно большому запросу виртуальной памяти и к пробуксовыванию. Мораль: при построении контурных линий некоторые ветви могут пропадать.

Вот что происходит при построении некоторых графиков.

График 
ImplicitPlot[
Sqrt[(х^2+у^2)^5]- 2*(Abs[у]+у)*(х^2+у^2)==0,

(х,-10,10},{у,-10,10},
PlotPoints->300];//Timing

вообще выглядит пустым. График же

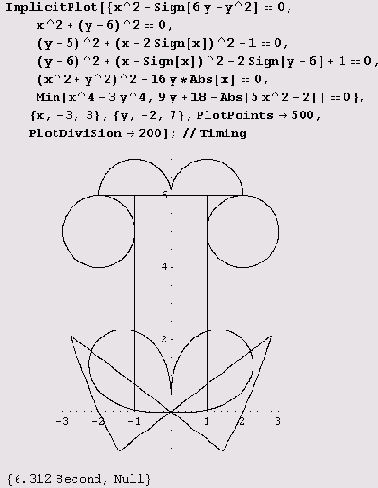
рисуется, но не без проблем: некоторые параметры (PlotPoints->500, PlotDivision->200) пришлось подбирать, иначе мелкие штрихи пропадают. Еще большие проблемы возникают при вычерчивании следующего графика.

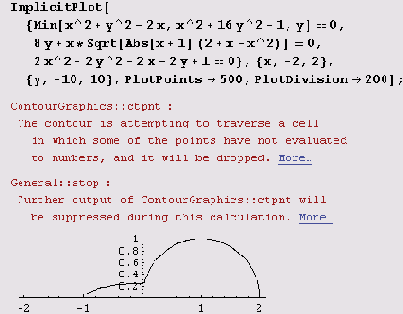
График же

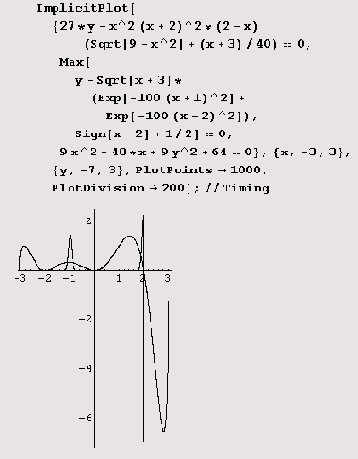
вычерчивается без проблем.

Так же легко вычерчивается и следующий график.

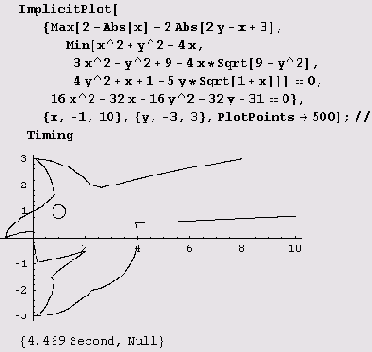
График же

построению почти не поддается: при изменении параметров PlotPoints->l000, PlotDivision->2500 в нем часто исчезают те или иные детали. Не удается его построить ни вот так 
ImplicitPlott((х+4)^2+1-Sigm[1-у^2])
((х+3)^2+у^2+2Sign[х+3]+1)




((2х+3)^2+у^2-1)((х^2-х)^2-Sign[1-у^2]+1) 
(у^2+Sign[х^2-х]+1) ((х-3)^2+у^2+2Sign[х-3]+1)

((х-2)^2+(у-1)^2+Sign[2-х]+Sign[y-1]+1)

 ((х^2-9х+20)^2-Sign[1-у^2]+1)

((y+Abs[x-4]+Abs[x-5])^2-Sign[(х-4)(21/4-х)]+1)==0,

(х,-4,5},

PlotPoints->1000,PlotDivision->250];

ни вот так 
ImplicitPlott{(х+4)^2+1-Sign[1-у^2]==0,

 (х+3)^2+y^2+2Sign[х+3]+1==0,

 (2х+3)^2+у^2-1==0, (х^2-х)^2-Sign[1-у^2]+1==0,

y^2+Sign[x^2-x]+l==0, (х-3)^2+y^2+2Sign[x-3]+l==0,

(x-2)^2+(y-l)^2+Sign[2-x]+Sign[y-l]+l==0,

(х^2-9х+20)^2-Sign[l-y^2]+l==0,

(y+Abs[x-4]+Abs[x-5])^2-Sign[(x-4)(21/4-х)]+1==0},

{х,-4,5},PlotPoints->1000,

PlotDivision->250];

В лучшем случае получаем кучу предупреждений и вот что.

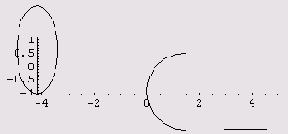
Мораль: графики многих неявных функций легко строятся с помощью функции ImplicitPlot, однако существуют невинно выглядящие мехматовские "приколы", при построении которых либо теряются дуги, отдельные точки, отрезки, либо же графики не строятся совсем. Иногда проблем удается избежать, если изменить метод построения графика (от решения уравнения перейти к построению линии уровня или наоборот). Однако это помогает далеко не всегда. Тогда приходится брать мехматовские учебники. Они не покажутся такими недоступными, если вы будете читать их, а система Mathematica будет делать то, что там написано! Очень часто всего лишь нескольких подстановок (их может выполнить система Mathematica) достаточно, чтобы перейти к параметрическому заданию графика.


Несколько графиков на одном чертеже — функция GraphicsArray



Как вы уже знаете, функция GraphicsArray позволяет на одном листе (чертеже) нарисовать несколько графиков, расположив их в одну строку или в виде двухмерного массива. Однако если вы все графики вычерчиваете с помощью одной функции, например ParametricPlot, удобно предварительно установить те значения ее опций, которые совпадают у большинства графиков. Пусть, например, мы хотим установить опции AspectRatio->Automatic и Axes->False. Вот как это делается.

SetOptions[ParametricPlot,AspectRatio->Automatic,Axes->False] ;

Теперь можем определить нужные нам графики и при необходимости задать значения тех опций, которые отличаются от установленных ранее. Пусть, например, на первом и третьем графиках вычерчиваются оси координат. Тогда для этих графиков устанавливаем Axes->True. 

Block[{$DisplayFunction=Identity},

pl=ParametricPlot[{Cos[t],Sinft]},{t,0,2Pi},Axes->True];

p2=ParametricPlot[{2Cos[t],Sin[t]),{t,0,2Pi}];

p3=ParametricPlot[{ (2Cos [t] -1) Cos [t-] , (2Cos [t]-1) Sin [t] },

{t,0,2Pi},Axes->True];

p4=ParametricPlot[{t Cos[t],t Sin[t]},{t,0,12Pi}];

p5=ParametricPlot[{t Cos[t]Sin[t],t Sin[t]Л2},{t,0,8Pi}];

 p6=ParametricPlot[{Sin[2t]+Sin[5t],Cos[2t]+Cos[5 t]},{t,0,2Pi}];

p7=ParametricPlot[{Sin[2t]Sin[5t],Cos[2t]Sin[5t]},{t,0,2Pi}];

p8=ParametricPlot[{Cos[t]+l/2Cos[7t]+l/3 Cos[-17t+Pi/2],

Sin[t]+l/2 Sin[7 t]+l/3Sin[-17t+Pi/2]},{t,0,2Pi}];]

После этого формируем массив фафиков и отображаем его.

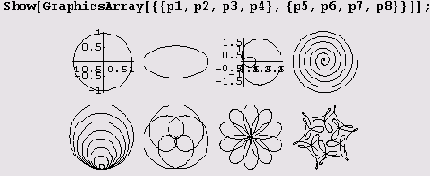
Функция GraphicsArray может быть полезна при подборе параметров.

Пример 9.18. Подбор параметров с помощью функции GraphicsArray. Предположим, вам нужно среди двухпараметрического множества кривых (напоминающих цветы) вида (R cos(az), R sin(fe)), где R = sin 5r, выбрать ту, которая ближе всего к окружности при условии, что параметры а и b принимают целые значения, причем 1<а<9 и 1<6<6. Можно, конечно, пересмотреть все 54 кривые по одной. Но если вы не уверены, что среди них есть окружность, лучше расположить все графики на одном чертеже. Однако в отличие от предыдущих примеров, где количество графиков было небольшим, в данном случае формирование массива лучше всего поручить системе Mathematica. Для этого как нельзя лучше приспособлена функция Table. Именно с ее помощью удобнее всего сначала сформировать двухмерный массив шириной 6 и высотой 9 графиков. Затем эти графики лучше всего отобразить на одном чертеже и выбрать (на глаз) те, которые, как вам кажется, наиболее подходят для вашей цели. Отобранные графики затем можно будет рассмотреть в деталях и выбрать наиболее подходящий из них. Вот как это делается в нашем случае. 
Block[{k=5},Block[{a,b,r=Sin[k*z]},

Block[{XY={r*Cos[a*z],r*Sin[b*z]}),

Show[GraphicsArray[ Table[Table[ParametricPlot[XY,{z,0,2 Pi}],
{b,6}],{a,9}]]]]]]

Когда будете выполнять эту программу, перед вами промелькнет 54 графика, которые рассмотреть вы, конечно, не успеете. Зато в конце вы увидите следующую картинку.

Я думаю, вы без труда найдете здесь окружность.

Конечно, в рассмотренном примере нам немного повезло. Ведь параметры были последовательными натуральными числами. Благодаря этому было так легко организовать перебор их значений с помощью параметра функции Table. Но что делать, если нужно вычертить, скажем, четыре десятка кривых, параметры которых просто заданы таблицей?

Пример 9.19. Циклоиды. Пусть семейство циклоид задается параметрическим уравнением
ф — поворот вокруг начала координат на угол φ. Пусть параметры г,, г2 и а заданы таблицей (всего 40 наборов параметров в таблице).

№ n/n
 r1
 r2
 а
1
 2
 -1
 1
2
 3
 - 1
 1
3
 3
 -2
 2
4
 4
 -1
 1
       


Как начертить все нужные нам кривые, не задавая в их уравнениях параметры вручную? Для этого придется превратить таблицу в список наборов параметров.

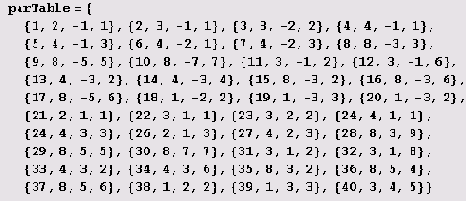
Заметьте, что порядковый номер включен в набор параметров первым элементом. Это значительно облегчает поиск нужного набора параметров в таблице. Теперь мы хотим написать программу, которая печатает на одном чертеже графики с порядковыми номерами в заданном диапазоне, располагая их по т штук в ряду.

Сначала определим вращающийся единичный вектор.

Rphi[phi_]:={Cos[phi],Sin[phi]}

После этого можно дать определение функции PolarXYAB для наших циклоид.

PolarXYAB[t_,г 1_,r2_,a_,omega_]= r1+r2*Rphi[t]+a*Rphi[omega*t]

Теперь определим функцию, рисующую отдельный график. 

gg[n_]:=Block[{plot,rl=parTable[[n]] [[2]],r2=parTable[[n]] [ [3]],

a=parTable[[n]] [[4]]},

plot=ParametricPlot[PolarXYAB[t,rl,r2,a,omega],

{t,0,2 Denominator[omega]Pi}, Axes->False,

PlotLabel->"n="oToString [n] ] ]

Теперь можем нарисовать, например, первые 15 циклоид, параметры которых соответствуют порядковым номерам с 1 по 15 в нашей таблице. (Они все будут круговыми циклоидами.) Вот как это делается. 
Block[{n,m=5,omega=l/7},

Show[GraphicsArray[

Table[Table[gg[n=(a-l)*m+b],{b,m}],{a,3}]]]]

Перед вами промелькнут 15 графиков, а в конце вы увидите вот что.

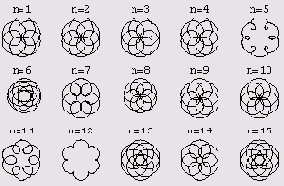
Чтобы начертить графики 16 и 17, в программе изменяется лишь m и начальный порядковый номер. 
Block[{n,m=2,omega=l/7},

Show[GraphicsArray[

Table[Table[gg[n=15+(a-1)*m+b],{b,m}],{a,!)]]]]

В конце вы увидите следующее.

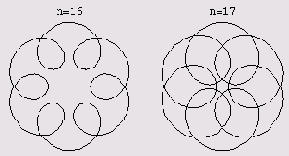
Это развернутые циклоиды. Нарисуем, наконец, развернутые циклоиды, которые образуются, когда подвижная окружность содержит внутри себя неподвижную. (Это графики с 18 по 20.) 
Block!{n,m=3,omega=l/7},

Show[GraphicsArray[

Table[Table[gg[n=17+(a-1)*m+b],{b,m}],{a,1}]]]]

В результате вы увидите вот что.

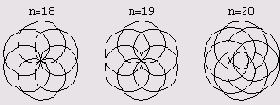
Теперь нарисуем 2 ряда развернутых циклоид. (Это графики с 20 по 30.) 
Block[(n,m=5,omega=l/7),

Show[GraphicsArray[

Table[Table[gg[n=20+(a-1)*m+b],{b,m}],{a,2}]]]]

Вы увидите следующее.

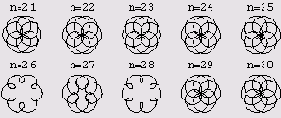
Вспоминаем, наконец, об оставшихся 10 графиках. В программе достаточно изменить лишь начальный порядковый номер. 
Block[{n,m=5,omega=l/7},

Show[GraphicsArray[

Table[Table[gg[n=30+(a-1)*m+b],{b, m}], {a, 2}]] ] ]

А вот и сами графики.

Графические примитивы и опции трехмерной графики



Если вместо заголовка Graphics воспользоваться заголовком Graphics3D, то можно получать трехмерные рисунки. При этом примитивы Point, Line, Text и Polygon с учетом третьей координаты переносятся на трехмерный случай.

Рисуем параллелепипед — графический примитив Cuboid

Единственным новым трехмерным примитивом является Cuboid [ {xmin, ymin, zmin], {xmax, ymax, zmax} ], с помощью которого рисуется параллелепипед, противоположные вершины которого имеют координаты (xmin, ymin, yniri) и (xmax, ymax, zmax).

Как и в двухмерном случае, рисунок создается с помощью примитивов. -

Опции трехмерной графики

Многие опции являются общими для функций двухмерной и трехмерной графики. К таким опциям относятся AspectRatio, Axes, AxesLabel, AxesStyle, Background, Color-Output, DefaultColor, DisplayFunction, Epilog, PlotLabel, PlotRange, PlotRegion и Ticks. Опишем теперь те опции, которые присущи именно функциям трехмерной графики.

Координатный параллелепипед, или коробочка, — опция Boxed

Обычно графики трехмерных объектов заключаются в коробочку. Однако от нее иногда лучше отказаться. Для этого укажите опцию Boxed->False.

Закрашивание поверхности — опция Shading

Опция Shading устанавливает или отменяет закрашивание поверхности в серый или иные цвета в зависимости от расположения соответствующего участка поверхности. Если установить Shading->False, то представление о поверхности можно получить по имеющейся на ней криволинейной сетке, образованной линиями пересечения плоскостей х = const и у = const с поверхностью.

В случае Shading->True окраска поверхности определяется высотой точки поверхности или освещением (опция Lighting->True).

Дополнительное освещение (опция Lighting), его тип (опция AmbientLight) и источники света (опция LightSources)

Опция Lighting определяет, будет ли использована искусственная подсветка двухмерной поверхности. Если установлено Lighting->True, то тип подсветки определяется опцией AmbientLight (фоновый цвет), а координаты источников света — опцией LightSources (источники света).

С помощью опции AmbientLight->GrayLevel [уровень освещения] (неотрицательное число уровень освещения не должно превышать 1) осуществляется равномерное окрашивание поверхности в серый цвет, а если установить AmbientLight->Hue [оттенок] (неотрицательное число уровень освещения не должно превышать 1), осуществляется окрашивание в указанный оттенок (цвет Hue-палитры). Можно также указать Пие[оттенок, насыщенность, яркость] (неотрицательные числа оттенок, насыщенность, яркость не должны превышать 1). Hue [h] эквивалентно Hue [h, 1, 1].

В то же время может осуществляться подсветка поверхности источниками света различной окраски, расположенными в точках с заданными координатами (х, у, г}. Вот пример.

По умолчанию сделаны установки AmbientLight->GrayLevel [0] и LightSources->{(U.,0.,1.}, RGBColor[1,0,0]}, {{l.,l.,l.}, RGBColor[0.,1.,0.]}, { {0 . ,1.,1.}, RGBColor[0.,0.,1]}

При установке Lighting->False точки поверхности с меньшими значениями координаты z подкрашиваются в более темные оттенки серого.

Точка зрения — опция ViewPoint

Опция viewEoint определяет точку зрения (называемую также центром перспективы, центром проекций или полюсом), т.е. ту точку, из которой рассматривается сцена. Иными словами, все объекты рисуются так, как они видны из этой точки. Координаты точки зрения задаются в специальной системе координат, центр которой находится в центре коробочки. Иными словами, центр коробочки в этой системе координат имеет координаты {0,0,0}. Длина единичного орта этой системы координат равна наибольшей стороне коробочки. По умолчанию задана опция ViewPoint->{l.3,-2.4,2). Часто выбираются следующие координаты точки зрения: {0, -2,0} — вид спереди (на фасад коробочки), {0, -2,2} - вид сверху спереди, {0, -2, -2} — вид снизу спереди, {-2, -2, 0} — вид из левого угла, {2, -2,0}— вид из правого угла, {0,0,2} — вид сверху. Точка зрения должна находиться вне коробочки. Чем дальше находится центр проекций от сцены, тем меньше искажения вследствие центрального проектирования. Чтобы получить представление, как изменяется рисунок при изменении точки зрения, сравните следующие два графика.



Коробочка, ее размеры (опция BoxRatios) и положение на рисунке (опции ViewCenter и ViewVertical)

Относительные размеры других сторон коробочки определяются опцией BoxRatios. Чтобы увидеть, как эта опция влияет на вид графика, сравните следующие два рисунка.

Положение коробочки в поле, отведенном для рисунка, определяют опции ViewCenter-и ViewVertical. Если установить ViewCenter->{!/2, 1/2, 1/2}, центр коробочки будет помещен в центр рисунка. По умолчанию установлено View-Center->Automatic, при этом центр коробочки находится в центре рисунка. Координаты центра коробочки могут принимать значения от 0 до 1.

Опция viewVertical указывает направление, которое будет считаться вертикальным в окончательном рисунке. Настройка по умолчанию ViewVertical->{0, 0, 1} определяет, что в основной' системе координат вертикальной осью будет ось аппликат (ось z)- Координаты вектора, указывающего вертикальное направление, могут принимать значения от 0 до 1. Ниже одна и та же поверхность изображена в разных положениях.



Сетка — опция Mesh

Иногда криволинейная сетка линий мешает рассмотреть поверхность. Чтобы убрать сетку, установите Mesh->False.

Раскраска гор и впадин — опция ColorFunction

Интенсивность и цвет точки на поверхности зависят от ее координаты z и определяются опцией ColorFunction. По умолчанию ее значение равно Automatic.

Отображение отсекаемых частей — опция ClipFill

Если значение функции в какой-то области выходит за диапазон, указанный в опции PlotRange, часть поверхности отсекается. Опция ClipFill определяет, как будут отображаться плоскости отсечения. Если установить dipFill->Automatic, то плоскости отсечения будут отображаться так же, как и сама поверхность. Иными словами, те части поверхности, которые выходят за диапазон, указанный в опции PlotRange, заменяются частями отсекающих плоскостей. Части отсекающих плоскостей как бы становятся крышей (или дном) над (соответственно под) теми областями, над (под) которыми поверхность отсекается.

Если установить dipFill->None, то плоскости отсечения не будут отображаться вообще. Иными словами, те области, над (или под) которыми поверхность выходит за диапазон, указанный в опции PlotRange, окажутся без крыши (или дна).

Если установить clipFill->цвет, то плоскости отсечения будут окрашены в указанный цвет. Иными словами, дно и крыша окрашиваются в указанный цвет.

Если все же хотите раскрасить потолок и пол (крышу и дно) в разные цвета, их придется указать вот так: ClipFill->{ цвет пола, цвет потолка}.

Отображение скрытых поверхностей — опция HiddenSurface

Объекты, расположенные ближе, могут скрывать те, которые расположены от наблюдателя дальше. Очень часто части поверхности, расположенные ближе, скрывают те, которые расположены дальше. По умолчанию опция HiddenSurface равна True. В этом случае поверхность подсвечивается и подкрашивается так, как если бы она была поверхностью непрозрачного тела. Конечно, при этом с выбранной точки зрения некоторые участки поверхности могут быть невидимы. Убрав раскраску, их можно сделать видимыми. Для этого установите опцию HiddenSurface->False.

 

Вычерчивание графиков



Для вычерчивания графиков образов в трехмерном пространстве чаще всего используются следующие функции трехмерной графики: Plot3D, ParametricPlot3D и ListPlot3D.

Построение графика функции двух переменных

Простейшими способами задания функции двух переменных являются явный (т.е. в виде равенства z=fix, у)) и табличный. Для изображения графика функции двух переменных, заданной в виде равенства z=fix, у), предназначена функция Plot3D, a графики таблично заданных функций двух переменных можно начертить с помощью функции ListPlot3D.

Построение поверхности, заданной уравнением z = f(x, у), — функция Plot3D

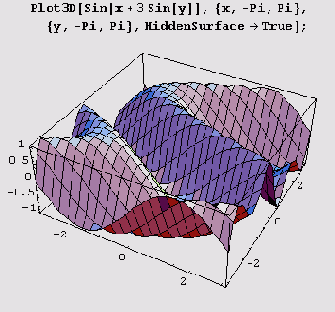
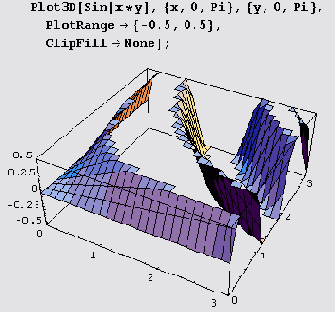
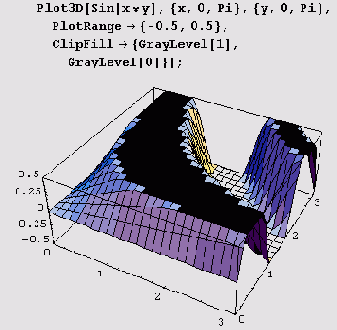
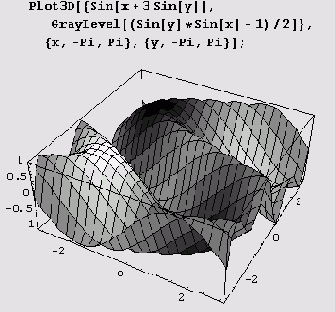
Вызов Plot3D[/, [х, xmin, xmax}, (у, ymin, ymax}} генерирует график/как функции х и у. То же самое делает и вызов Plot3D[{/, оттенок], (х, xmin, xmax), {у, ymin, ymax} ], но при этом указывается оттенок графика. Функция оттенок должна возвратить одну из директив GrayLevel, Hue или RGBColor либо объект SurfaceColor. На приведенном ниже рисунке с помощью функции оттенок на пересеченной местности, описываемой уравнением z = sin(x+3 sin у), нанесены "солнечные пятна" и "тени" (по всей видимрсти, от туч).

Построение графика таблично заданной функции двух переменных — функция ListPlot3D

Функция ListPlot3D служит для построения графика таблично заданной функции двух переменных. Вызов функции имеет вид ListPlot3D [таблица] или ListPlot3D [таблица, таблица оттенков]. Таблица должна быть прямоугольным массивом вещественных чисел. Иными словами, она должна быть списком списков одинаковой длины. Числа в ней интерпретируются как значения функции. Если таблица имеет размер /пхл, то таблица оттенков должна иметь размер (m- 1)х(n- 1). Элемент таблицы оттенков и в самом деле должен быть оттенком — он должен либо быть объектом SurfaceColor, либо иметь тип GrayLevel, Hue или RGBColor. Ниже показан горный ландшафт, сгенерированный с помощью таблицы функции г = е~5а*'у, к которой добавлены случайные возмущения.

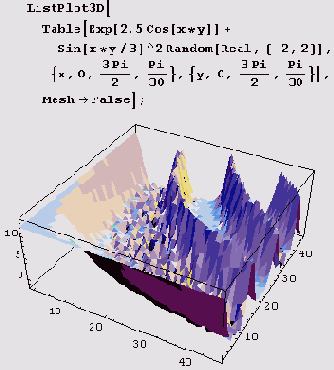
Построение параметрически заданных кривых и поверхностей — функция ParametricPlot3D

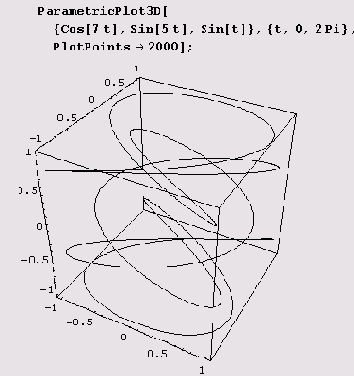
Далеко не все поверхности можно задать уравнением z = f(x,y)) или таблично. Часто гораздо удобнее задавать их параметрически. Параметрически можно задать также кривые в пространстве. Параметрически заданные в трехмерном пространстве двухмерные поверхности или одномерные кривые можно рисовать с помощью функции ParametricPlot3D. Проекцией нарисованной ниже кривой является фигура Лиссажу.

Вызов ParametricPlot3D[ {xt, yt, it], {t, tmin, tmax}] возвращает пространственную кривую, параметризованную переменной /, изменяющейся от tmin до tmах.

Вызов же ParametricPlot3D[ {xt, yt, zt}, {t, tmin, tmax}, {u, umin, umax}] возвращает поверхность в пространстве, параметризованную переменными t и и, изменяющимися от tmin до tmax и от umin до итах соответственно. Можно указать оттенок рисуемого образа, для этого вызов нужно записать так: ParametricPlotSD [{xt, yt, zt, оттенок}, ...]. Ну и, конечно, можно нарисовать несколько образов. Для этого вызов записывается так: ParametricPlotSD [{(xlt, ylt, zJt}, (x2t, y2t, z2t), ...}, ...]. На рисунке ниже хорошо видно, что кривые x=tcost, y=tsint, z= 2t и х= 2 t cos t, у = 2t sin t, z = 2 t лежат на конусах.

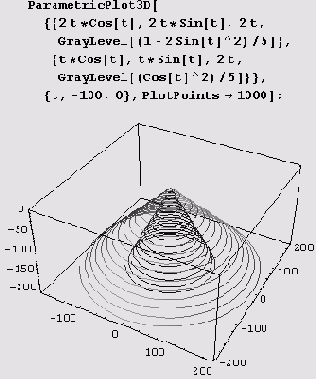
Для оттенения этих конических винтовых линий (создания эффекта их освещения) применялась функция GrayLevel. Это "освещение" несколько необычно: там, где одна коническая винтовая линия темнеет, вторая светлеет.

На следующем рисунке показаны конусы с общей вершиной.

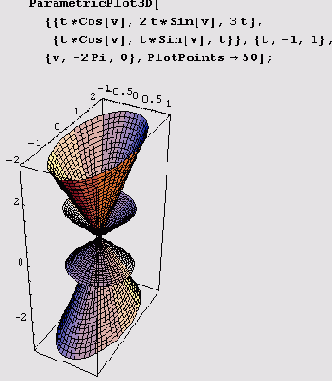
Поверхности вращения — пакет Graphics`SurfaceOfRevolution`

Для рисования поверхностей вращения удобнее применять пакет Graphics`SurfaceOf Revolution`, который загружается как обычно: <<Graphics`Surf асеOf Revolution`. Вызов SurfaceOfRevolution [t, {x, xmin, xmax}] строит поверхность, которая получается в результате вращения кривой z = f(x) вокруг оси аппликат. Вот пример.

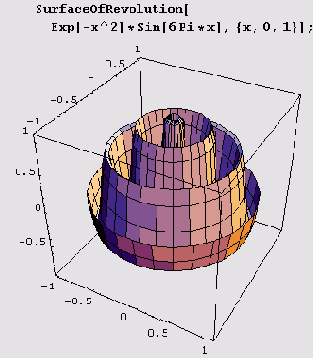
Вращать можно и плоскую параметрически заданную кривую х = fx(t), у = fy(t), но тогда вызов нужно записать вот так: SurfaceOfRevolution[ (fx, fy], {t, a, b}].

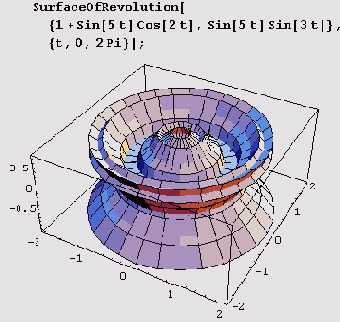
Более того, вращать можно и пространственную параметрически заданную кривую x=fx(t), у = fy(f), z=fz(t), но тогда вызов нужно записать вот так: SurfaceOf Revolution[ [fx, fy, ft}, {t, a, b)].

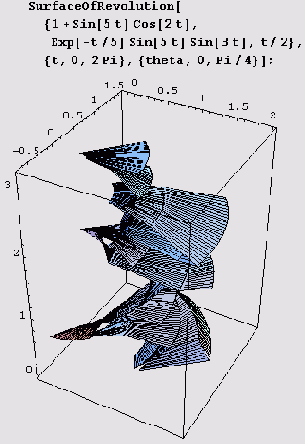
Иногда нужно нарисовать не всю поверхность вращения, а только ее часть, соответствующую углам вращения в, таким, что θ min< θ < θmax . Тогда в вызов нужно добавить диапазон углов (theta, thetamin, thetamax}. Например, в случае поверхности, образованной вращением кривой, заданной уравнением у =f(x), вызов нужно записать так: SurfaceOfRevolution[t, {х, xmin, xmax}, {theta, thetamin, thetamax}}. Конечно, аналогичное добавление нужно сделать и для случаев параметрического задания вращаемой кривой. Ниже представлено изображение абстрактной скульптуры, полученное таким способом из параметрически заданной пространственной кривой.

Наконец, иногда нужно указать ось вращения, проходящую через начало координат. Для этого можно воспользоваться опцией RevolutionAxis. Если ось вращения лежит в плоскости xOz, то в опции RevolutionAxis достаточно указать координаты х и г точки, отличной от начала координат: RevolutionAxis->{x, r). В иных случаях придется указать все три координаты любой, отличной от начала координат точки, инцидентной оси вращения: RevolutionAxis->{x, у, r)

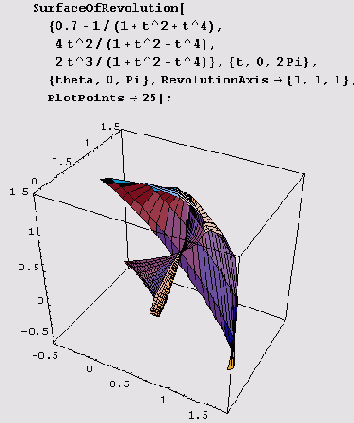
Вращать, конечно, можно и таблично заданные кривые. Для этого предназначена функция ListSurfaceOfRevolution. Вот возможные обращения к ней: 

ListSurfaceOf Revolution [{точка1, точка2,...}},

ListSurfaceOfRevolution [{точка1,точка2, ...},

(theta, thetamin,thetamax}}.


Другие миры — другие измерения



Жаль, конечно, расставаться с геометрией двухмерного и трехмерного миров, ведь мы еще только начали знакомиться с возможностями системы Mathematica в этой области. Но все же прежде чем перейти к другим разделам математики, поговорим немного о других измерениях. Прежде всего это время. И потому мы собираемся поговорить немного об изменяющихся во времени геометрических образах.


Четвертое измерение — время. Движущиеся картинки — кино



Система Mathematica позволяет проводить визуализацию динамических процессов. Серию графических рисунков можно оживить подобно тому, как из серии неподвижных картинок-кадров можно- создать мультфильм. Технологию создания мультфильма продемонстрируем на простом двухмерном примере: бегущей синусоидальной волне.

Мультипликация. Немой мультфильм "Бегущая волна"

Мультипликация является единственным подлинным искусством в настоящее время. Потому что в ней, и только в ней, художник абсолютно свободен в своей фантазии и может делать все, что угодно.

Чарли Чаплин

Создание мультфильма выполняется в два этапа. Сначала нужно создать рисунки, т.е. выполнить раскадровку, а затем смонтировать их.

Раскадровка

Сначала сделаем серию из 11 рисунков, каждый из которых представляет собой график функции Sin [x-t] на отрезке оси х от 0 до 4n для / = 0,2n/10, 4n/10, ..., 2mс. Вы и оком моргнуть не успеете, как эти рисунки будут помещены в последовательные ячейки блокнота.

Table[Plot[Sin[x-t],{х,0,2Pi}],(t,0,2Pi,2P1/10}]; Раскадровка выполнена!

Секреты раскадровки

При подготовке рисунков к анимации следует проявить известную предусмотрительность.

Секреты раскадровки двухмерных образов

Совсем не обязательно, чтобы области значений функций для всех графиков совпадали. Однако если они совпадать не будут, то при автоматическом выборе ее эффекты увеличения или уменьшения объекта могут не воспроизводиться. Вместо этого вы увидите растяжение (или сжатие) масштаба на осях. Если это не желательно, нужно установить подходящее значение опции PlotRange. Очень часто в качестве ее значений устанавливаются константы, обеспечивающие обзор всей сцены.

Секреты раскадровки трехмерных образов

Для трехмерных образов есть еще один источник нежелательных эффектов: перемещение коробочки с графическим объектом. Это может создать впечатление, что сцена прыгает! Чтобы устранить этот эффект, нужно установить опцию SphericalRegion -> True, обеспечивающую неподвижное положение коробочки (сцены) с графическим объектом во всех рисунках.

Монтаж

Монтаж выполняется очень просто: нужно выделить все 11 ячеек блокнота с кадрами.

Просмотр

Чтобы просмотреть смонтированный таким образом мультфильм, достаточно нажать <Ctrl+Y> или выбрать команду Ячейка<=>Анимация Видео. В той ячейке, которая полностью видна на экране дисплея, будет начата демонстрация фильма. Внизу экрана при этом появятся шесть кнопок, которые позволяют изменить направление времени (прокрутить фильм в обратном направлении), ускорить, замедлить показ или приостановить его.

Еще одно измерение — звук



В системе Mathematica предусмотрены различные способы задания и воспроизведения звука.

Воспроизведение звука с аналитически заданной амплитудой — функция Play

Вызов функции Play[/, {t, tmin, tmax}} запускает проигрывание звука. Амплитуда звука определяется функцией времени f(t), причем t изменяется между tmin и tmax. (Единица измерения— секунда.) Например, вызов Play [Sin[220*2*Pit], {t, 0,1} ]; проигрывает чистый тон (частоты 220 Гц) в течение 1 с. Вызов Play [ {/7, /2}, {t, tmin, tmax}] проигрывает стереозвук, причем// задает левый канал, t2 — правый. Для проигрывания многоканального звука используется вызов вида Р1ау[{t2, t2, ...}, ...}. Частота оцифровки задается в опции SampleRate. По умолчанию она равна 8192. Количество бит, используемых для запоминания амплитуды, можно указать в опции SampleDepth. По умолчанию оно равно 8. Диапазон проигрываемых амплитуд можно указать в опции PlayRange. Есть также опции Prolog и Epilog. По умолчанию они равны {}.

Воспроизведение звука с таблично заданной амплитудой — функция List Play

Вызов функции ListPlay [список] запускает воспроизведение звука. Значения амплитуды звука задаются списком. Вызов ListPlay [{список1, список2}] воспроизводит стереозвук, причем список1 задает левый канал, а список2 — правый. Для проигрывания многоканального звука используется вызов вида ListPlay [ {список1, список2, ...}]. Частота оцифровки задается в опции SampleRate. По умолчанию она равна 8192. Количество бит, используемых для запоминания амплитуды, можно указать в опции SampleDepth. По умолчанию оно равно 8. Диапазон проигрываемых амплитуд можно указать в опции PlayRange. Есть также опции Prolog и Epilog. По умолчанию они равны {}. Вот как можно прослушать число я.

Честно говоря, каких-либо существенных отличий от белого шума я найти не смог.

Функция ListPlay генерирует примитив SampledSoundList, который может использоваться внутри объектов Sound, Graphics и Graphics3D. SampledSoundList [{а1, а2, ... }, r] представляет собой оцифрованный звук с амплитудами а,, аb ..., причем частота оцифровки равна гГц.

Кроме того, есть специальный пакет Miscellaneous`Audio4`, в котором предусмотрены самые разнообразные функции как для создания, так и для обработки звуков.


с поддержанной многими выдающимися математиками



В соответствии с поддержанной многими выдающимися математиками концепцией Давида Гильберта, математика может обойтись без чертежей и графиков, а тем более без мультимедиа. Но многие выдающиеся математики (в их числе и Давид Гильберт), не говоря уже о выдающихся художниках-математиках (таких, как Анатолий Тимофеевич Фоменко), всегда объясняли самые абстрактные идеи математики с помощью не только выкладок, но и ярких, часто цветных чертежей и рисунков — подлинных произведений изобразительного искусства. Это и понятно. Ведь не только, а подчас и не столько формулы служат стимулом для генерации новых идей, сколько яркие, запоминающиеся образы. И в системе Mathematica предусмотрены разнообразные средства создания графиков, чертежей и даже произведений компьютерного искусства, способных удовлетворить самый изысканный вкус и оживить лекцию по самым абстрактным разделам математики. Что же касается других наук, как естественных, так и гуманитарных, то здесь без средств визуализации данных просто не обойтись. И уж совсем невозможно представить себе инженерную деятельность и производство без чертежей. И потому в системе Mathematica есть не только традиционные средства построения графиков функций одной и нескольких переменных, но и средства построения разнообразных диаграмм, применяемые представителями гуманитарных наук. Кроме того, система Mathematica умеет работать со звуком, и в ней легко проводить визуализацию динамических процессов.