Алгебра и пакет Mathematica 5
Замена выражений в формулах
Одним из наиболее распространенных видов алгебраических преобразований является замена выражений, часто называемая также подстановкой, в результате выполнения которой какая-либо часть алгебраического выражения заменяется новым выражением. В системе Mathematica предусмотрено два способа подстановок. Первый способ выполняется с помощью функции
Set.
Вычисление выражения Set [левая часть, правая часть], или левая часть = правая часть, выполняется следующим образом. Сначала вычисляется правая часть, а затем получившийся результат (вычисленное выражение) присваивается в качестве значения невычисленной левой части. Всюду в дальнейшем левая часть, в какие бы выражения она ни входила, будет заменяться выражением, полученным в результате вычисления правой части. Левая и правая части могут быть списками, и поэтому операцию замены (подстановки)
Set можно записать в виде присваивания списков {левая часть,, левая часть2, ...} = {правая часть,, правая часть2, .. .}. В этом случае результат вычисления /-и правой части будет присвоен /-и левой части. В качестве примера присвоим символу х значение а и после этого вычислим выражение (х+1)^2.
х=а
а
(х+1)^2
(1 + а)2
Вот более сложный случай.
{х,х}={а,b}
{а,b}
х^2 b^2
Обратите внимание, что никакого предупреждения не было. Это подобно тому, как в языках программирования вполне допустим оператор х = х+1 потому, что действия выполняются не одновременно, а в определенном порядке.
А вот случай, когда значения функции задаются в определенных точках.
Evaluate[ff/@{a,b,с,d}]={1,23,45,678}; ff[b] 23
Как видите, теперь везде ff [b] заменяется своим значением. Пусть теперь b = 1. Заменится ли ff [1] своим значением? Оказывается, нет.
b=1
1
ff[l] ff[l]
Более того, теперь даже ff [b] не заменяется своим значением.
ff [b] ff1]
Это происходит потому, что аргумент функции вычисляется в данном случае раньше.
Иногда глобальную! подстановку нужно отменить. Если левая часть есть переменная, это можно сделать с помощью функции Clear. Вызов clear [переменная], переменная2, .. .} отменяет все подстановки значений, присвоенных переменным переменная!, переменная!, ... . Для отмены подстановки значения одной переменной можно использовать присваивание вида переменная = . b=N[Pi,50]
3.1415926535897932384626433832795028841971693993751
b=.
b
b
Присваивание вида переменная = . является синонимом выражения Unset [переменная].
b=N[Pi,50]
3.1415926535897932384626433832795028841971693993751
Unset[b]
b
b
Присваивание, или функция Set, задает глобальную подстановку, т.е. такую подстановку, которая выполняется во всех последующих вычислениях до ее явной отмены. Если же подстановку одного выражения вместо другого нужно сделать в одном конкретном выражении или же в нескольких, то удобнее использовать функцию Rule.
Выражение Rule [левая часть, правая часть], записываемое также в виде левая часть->правая часть, задает правило, в соответствии с которым вместо левой части подставляется вычисленная правая часть. При этом правая часть вычисляется в момент
вызова функции Rule. Если правую часть нужно вычислять в момент применения правила, то нужно вызвать не функцию Rule, а функцию RuleDelayed, вызов которой можно записать в виде левая часть :> правая часть.

Для всех дальнейших вычислений х сохраняет свое значение.
х+у
5.8598744820488384738229308546321653819544164930751+ у
Подстановки удобно задавать в виде поименованных правил. Например, можно определить подстановку r1= х->а, и после этого она может быть применена к конкретному выражению с помощью функции ReplaceAll, имеющей также постфиксную форму /.:
r1 = х -> а x+1/.rl
1+а
То же самое можно сделать и так:
ReplaceAll[х + 1, r1]
1+а
Вот пример последовательных замен.
{а,b, с}/.a->b/.b->d
{d,d,c}
Функция ReplaceAll позволяет осуществить несколько подстановок одновременно. Тогда эти подстановки должны быть оформлены в виде списка и заданы вторым аргументом этой функции. Вот пример одновременной замены:
{а,b,с}/.(a->b,b->d)
{b,d,c}
Однако функция ReplaceAll выполняет замену в каждом подвыражении только
раз, рекурсивно замена не выполняется.
а
ReplaceAll [х + х2 , {х -> а, х2 -> х} ]
а+х
Если же нужно делать подстановки повторно, необходимо использовать функцию
ReplaceRepeated.
ReplaceRepeated[x + х2, {х->а, х2-» х} ]
2 а
Функция ReplaceRepeated имеет постфиксную форму // ..
х + х2 // . {х -> а, х2 -> х}
2 а
Пусть имеем список заменяемых и список заменяющих выражений. Тогда правила замены можно сформировать с помощью функции Thread.
rr=Thread[{r,s,t}->{R, S,T}]
(r->R,s->S,t->T)
Теперь применим эти правила.
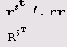
Выражения в системе Mathematica имеют заголовки. Например:
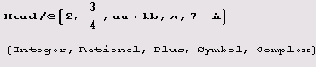
Их тоже можно заменить.

13 данном случае выражения с заголовками integer, Rational и Plus были заменены их логарифмами. Вот еще пример этого типа. Все выражения с заголовками f или g заменим их квадратами.
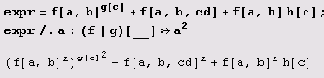
Вот еще один способ сделать то же самое.
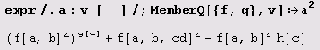
А вот как все множители, являющиеся вызовами функций, можно возвести в квадрат:
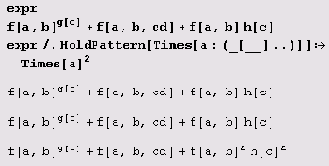
Заметьте, . что выражение HoldPattern [expression] эквивалентно выражению expression для сопоставления с образцом, но оставляет выражение expression в невычисленной форме.
А вот как все вызовы функций, не содержащие степеней и произведений, возводятся в куб.

Действия со степенями
Функция PowerExpand приводит (а*b) ^с к виду а^с * b^с. Преобразования, сделанные с помощью PowerExpand, корректны, вообще говоря, только если с целое, а а и b положительные.
Кроме того, PowerExpand приводит Log[а^b] к виду b*Log [а].
PowerExpand [Log [ (ab)n] ]
n (Log[a]+Log[b])
Квадратный корень тоже рассматривается как степень.
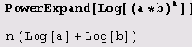
Ну и конечно же, PowerExpand также приводит (а^b) ^с к виду а^ (bc).
Раскрытие скобок
Раскрытие скобок выполняет функция Expand. Вот пример.
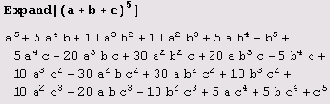
Можно указать, что при раскрытии скобок нужно выполнять приведение по определенному модулю.
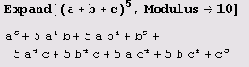
Наконец, можно указать, что раскрывать скобки нужно только в выражениях определенного вида. Для этого в вызове функции должен быть задан второй аргумент — шаблон, к которому применяется раскрытие скобок. Все выражения, не содержащие шаблона, останутся без изменения.
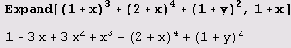
Однако функция Expand раскрывает не все скобки, а только в произведениях и степенях. Она не раскрывает скобки, например, в знаменателях. Если же нужно раскрыть все скобки, нужно применить функцию ExpandAll.

Конечно же, для функции ExpandAll также можно указать шаблон, к которому применяется раскрытие скобок. Все выражения, не содержащие шаблона, останутся без изменения.
Приведение подобных
Вызов Collect [expr, x] собирает в выражении ехрr члены с одинаковыми степенями х. Иными словами, функция Collect приводит подобные члены.
Collect[х+4у+5ху,х].
4 у+х (1+5 у), Collect[х+4у+5ху,у]
х+(4+5 х) у
Вызов Collect [ехрr, {x1, х2, ...}] собирает в выражении ехрr члены с одинаковыми степенями х{, затем — с одинаковыми степенями х2 и т.д.
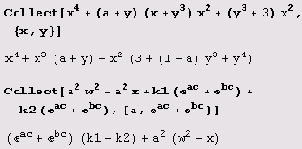
Иногда после приведения подобных нужно к каждому члену применить какую-нибудь функцию. Тогда ее нужно указать третьим параметром функции Collect: Collect [expr, {x1, х2, ...}, функция]. Вот как, например, выполняется разложение коэффициентов на множители после приведения подобных.
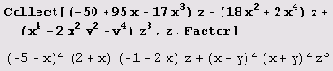
В функции Collect можно использовать шаблоны. В приведенном ниже примере они используются для того, чтобы собрать члены с одинаковыми степенями х и у.
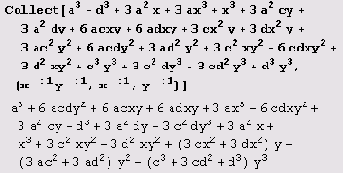
Заметьте, что полученное выражение отличается от
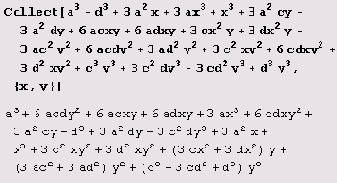
хотя и равно ему тождественно.
Ниже показано применение шаблона для того, чтобы собрать члены, содержащее производные функции z одинакового порядка.
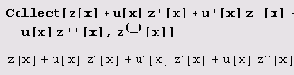
Многочлены
Чтобы проверить, что выражение ехрr есть многочлен по некоторой переменной
var, нужно вызвать функцию PolynomialQ [елрг, var]. Результат будет
True, если ехрr является многочленом по переменной var, и
False — в противном случае.
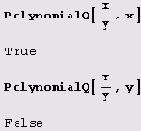
В случае нескольких переменных при проверке необходимо указать список переменных:
PolynomialQ [expr, [varl, var2,...}].
PolynomialQ[ху,{х,у}]
True
Выражение PolynomialQ [ехрr] равно True, если ехрr является полиномом относительно каких-либо переменных. В противном случае результат равен
False.
PolynomialQ[ху,{х,у}] True
PolynomialQ[(Pi+x)у] True
PolynomialQ[1/z+xy] False
Чтобы узнать общее число слагаемых в многочлене poly, можно вычислить выражение Length [poly]. Но не забудьте перед этим раскрыть скобки.
PolynomialQ[(a+b+c+d)^100]
True
Lengthf(a+b+c+d)^100] 2
Length[Expand!(a+b+c+d)^100]]
176851
Функция Variables, примененная к. poly, дает список всех независимых переменных в полиноме poly.
Variables[(a+b+c+d)^100]
{a,b,c,d}
Коэффициенты
Выражение Coefficient [poly, form] имеет своим значением коэффициент при выражении form в полиноме poly.
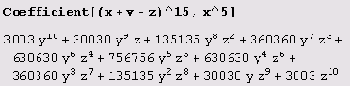
Выражение Coefficient [poly, form^n] эквивалентно Coefficient [poly, form, n].
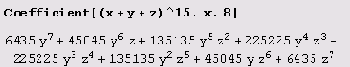
Результат вычисления выражения CoefficientList [poly, form] представляет собой список коэффициентов при степенях form в полиноме poly. Список составляется в порядке возрастания степеней.
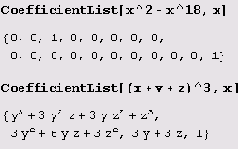
Список коэффициентов можно привести по определенному модулю.
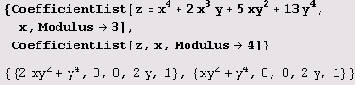
Приведение к каноническому виду
Приведение многочленов к каноническому виду выполняется путем раскрытия скобок и приведения подобных.
Разложение на множители
Разложение многочленов на множители над полем рациональных чисел выполняет функция Factor.
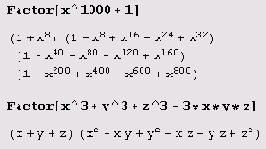
Разложение на множители выполняет не только функция Factor, но и функции FactorList и FactorTerms. В результате вычисления выражения FactorList [poly] получается список множителей полинома poly вместе с показателями степеней, с которыми множители входят в разложение poly на множители. Первый элемент списка есть общий численный множитель — так называемое содержание многочлена. Если содержание многочлена равно единице, то список начинается с {1,1}.
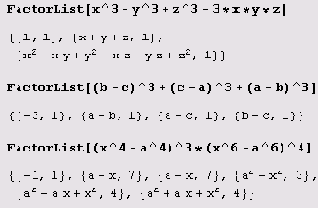
Функция FactorTerms позволяет вынести общий числовой множитель.
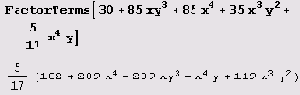
Вызов FactorTerms [poly, x] позволяет вынести общий множитель, не зависящий от х; FactorTerms [poly, {xl, x2, ...}] последовательно выделяет множители, не зависящие от x1, х2 и т.д. Вычисление выражения FactorTermsList [poly, (xl, x2, . . .}] дает список множителей poly. Первый элемент в списке есть общий числовой множитель, второй — множитель, не зависящий ни от одного из x1, х2, ... . Последующие элементы есть множители, не зависящие от как можно большего числа переменных x1, х2, ....
Деление многочленов
PolynomialQuotient [polyl, poly2] дает частное от деления многочлена poly1 на многочлен poly2, a PolynomialRemainder [poly1, poly2] — остаток.
Наибольший общий делитель многочленов
Важнейшими операциями при работе с полиномами являются нахождение наибольшего общего делителя и наименьшего общего кратного. Выражение PolynomialGCD [poly], poly2] представляет собой наибольший общий делитель многочленов polyl и poly2. При вычислении наибольшего общего делителя все символьные параметры в полиномах трактуются как переменные, и деление на них не допускается.
PolynomialGCD[х^3000-1, х^1503-1]
-1 + х3
Наименьшее общее кратное многочленов
Выражение PolynomialLCM[poly2, poly2] представляет собой наименьшее общее кратное многочленов poly1 и poly2.
Результант
Выражение Resultant [polyl, poly2, var] представляет собой результант многочленов poly1 и poly2, рассматриваемых как многочленов от переменной var.
Resultant[а*х^2+b*х+с, 2а*х+b, х] -
ab2 + 4 а2 с
Поле рациональных дробей
Дробь, числитель и знаменатель которой — полиномы, называется рациональной дробью. Уже знакомые нам функции
Expand и Factor могут применяться к рациональным дробям. Функция
Expand раскрывает произведения и целые положительные степени в числителе и представляет рациональную дробь в виде суммы дробей, знаменатели которых совпадают со знаменателем исходной рациональной дроби, а числителями этих дробей служат отдельные слагаемые в раскрытом числителе исходной рациональной дроби.
Функция Apart раскладывает рациональную дробь на простейшие.
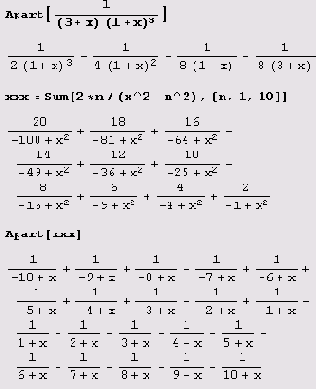
Функция Factor, примененная к сумме рациональных дробей, приводит их к общему знаменателю и раскладывает на множители числитель и знаменатель полученной рациональной дроби:

Функция Together приводит рациональные дроби к общему знаменателю и после их сложения сокращает общие множители в числителе и знаменателе.

Общие множители в числителе и знаменателе рациональной дроби не сокращаются автоматически. Чтобы их сократить. прибегают к функции
Cancel:
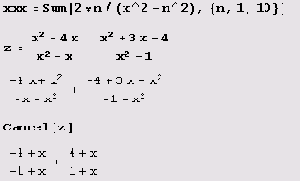
Можно раскрывать скобки только в числителе или только в знаменателе рациональной дроби. Для этого предназначены функции
ExpandNumerator и Expand Denominator. Получить числитель и знаменатель рациональной дроби можно с помощью функций
Numerator и Denominator, т.е. тех же самых функций, что используются для получения числителя и знаменателя рационального числа.
Для упрощения различных выражений, в том числе и рациональных, полезно применять функцию
simplify, которая выполняет алгебраические преобразования над выражением и приводит его к простейшей (с точки зрения системы Mathematica) форме. Данную функцию удобно применять в постфиксной входной форме, т.е. приписывая ее имя после
// в конце входного выражения:
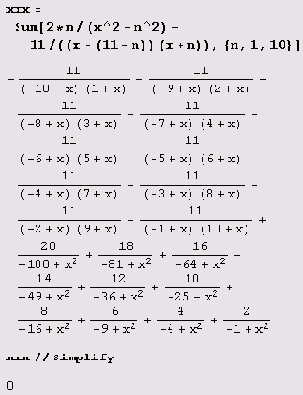
Функцию Simplify можно применять также для упрощения выражений при определенных условиях. Вот пример.
Simplify[a^3+b^3+c^3-3*a*b*c,a+b+c==0]
0
Линейная алгебра
Произведения векторов и матриц
Скалярное произведение векторов и матриц обозначается точкой.
{a1, а2, a3}.{b1, b2, b3}
a1 b1 + a2 b2 + аз bз
Для вычисления векторного произведения векторов применяется функция Cross. Она обозначается крестиком. Вот как вычисляется обобщенное векторное произведение пяти векторов в шестимерном пространстве.
{1,3,4,5,7,6}х{2,4,5,7,8,1}х{4,5,3,1,2,7}х {3,3,3,4,2,5}х{4,2,1,2,2,5} {522,-1076,1379,-580,60,-55}
Нормы векторов и матриц
С помощью функции Norm можно вычислять разнообразные нормы векторов и матриц.
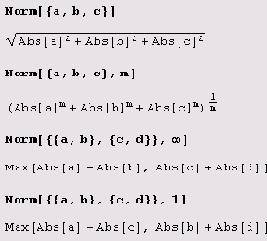
Обратные и псевдообратные матрицы
Совсем просто выполняется обращение неособенных матриц.
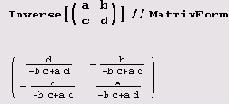
Особенная матрица не имеет обратной, но для нее можно определить псевдообратную, т.е. такую, произведение которой на исходную наименее уклоняется (по сумме квадратов) от единичной матрицы. (Конечно, для неособенной матрицы ее псевдообратная совпадает с обратной.)

С помощью псевдообратных матриц можно находить решения несовместных систем линейных уравнений.
Решение систем линейных уравнений
Пусть имеем систему линейных уравнений т х = v, где т — матрица системы, а v — вектор правых частей. Ее решение можно найти так.
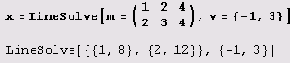
Вот как проверяется результат.
m.x-v
{0,0}
Имеются, конечно, и функции для специализированных методов, таких как Гауссово исключение, разнообразные декомпозиции, вычисление миноров и т.д.
Пределы
Для вычисления пределов предназначена функция Limit. Вот примеры нахождения нескольких пределов.

Абсолютно ничего сложного. Но помните, что если двустороннего предела нет, система Mathematica может пытаться подсунуть односторонний вместо него, причем даже предупреждения не будет! Вот тривиальный классический пример, показывающий, что в случае разных односторонних пределов система Mathematica в качестве
двустороннего предела просто подсовывает любой из односторонних.
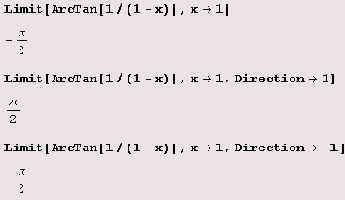
Дифференцирование
Для дифференцирования в системе Mathematica предусмотрена команда (функция) D [.,.]. Вот как вычисляется производная функции
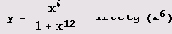
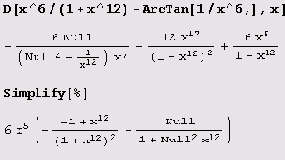
Заметьте, что выражение, полученное в результате дифференцирования, пришлось упрощать, так как автоматически упрощение не выполняется! Вот еще один пример.
0[Аbз[х^2],х]
2 Abs [x] Abs'[х]
Подход, я бы сказал, весьма формальный. (Зато он работает даже для функций комплексного переменного!) Из-за формализма вычисления зачастую могут выполняться не до конца.
D[Abs[х^2],х]/.х->1
2 Abs'[l]
Но в целом, если подобные примеры во внимание не принимать, система Mathematica успешно справляется и с вычислением частных (в том числе и смешанных) производных.
Для вычисления полных дифференциалов предусмотрена команда Dt.
Ряды
Разложение в ряд Тейлора
Вот как функция tg(x-x3)-sin(x+x3) разлагается в ряд Тейлора:
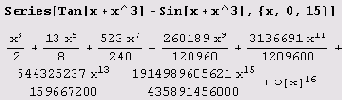
Чтобы отбросить остаточный член, можно воспользоваться командой Normal:
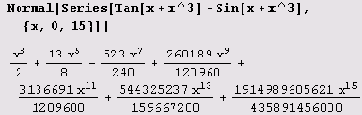
Ниже приведен пример разложения в ряд Тейлора функции двух переменных.
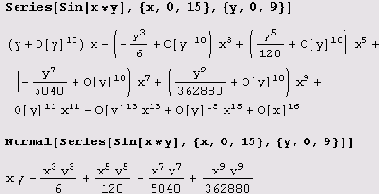
Заметьте, что для отбрасывания остаточных членов понадобилась только одна команда
Normal.
Арифметические операции над рядами
Конечно, ряды можно складывать, вычитать, умножать и даже делить. Причем все действия система Mathematica выполняет практически без дополнительных подсказок. Пусть имеем, например, два ряда Тейлора.

Деление можно выполнить так.
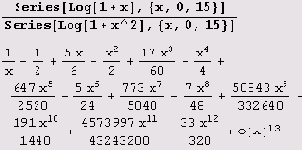
Конечно, это есть начальный отрезок ряда, представляющего частное функций.
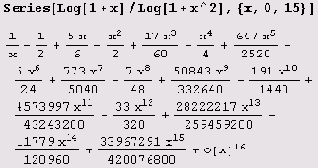
Исследование функций и построение графиков
Едва ли можно указать единую схему, пригодную для исследования абсолютно всех функций. Так что едва ли стоит удивляться, что в курсах анализа можно найти множество таких схем — от совсем кратких, похожих на весьма общие указания, до обширных, развернутых, с множеством всевозможных пунктов, в большинстве своем не имеющим никакого отношения к конкретной исследуемой функции. Однако все такие схемы обычно имеют несколько общих пунктов.
Определение интервалов возрастания и убывания функции
Найдем для примера интервалы возрастания и убывания функции у = x3-30x2+225x+l. Сначала определим функцию.
у=х^3-30*х^2+225*х+1
1 + 225 х - 30 х2 + х3
Данная функция — многочлен, поэтому она всюду дифференцируема. Найдем ее производную.
D[y,x] 225 - 60 х + 3х2
Так как и производная — многочлен, разложим его на множители.
Factor[%] 3 (-15+х) (-5+х)
Теперь видим, что производная отрицательна только на интервале (5; 15). На этом интервале функция, следовательно, строго убывает. На интервалах (-∞, 5) и (15, ∞) производная положительна. Поэтому на этих интервалах функция строго возрастает.
Нахождение локальных экстремумов
У рассмотренной нами функции у = х3-30x2+225с+1 производная обращается в нуль в точках х= 5 и х= 15. Поскольку это простые нули производной, то именно эти точки и являются точками ее локального экстремума. Легко вычислить значения функции в этих точках и построить ее график.
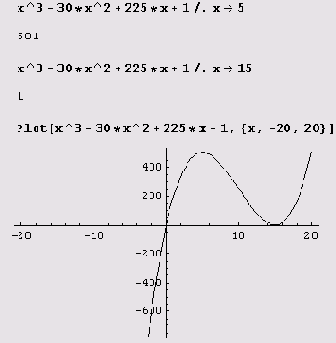
Вот более сложный пример. Пусть нужно найти локальные экстремумы функции
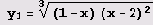
Определим нашу функцию в системе Mathematica.
y1=((l-x) (х-2)^2)^(1/3)
((1-х) (-2 + х)2)1/3
Данная функция определена и непрерывна на всей числовой оси. Находим ее производную.
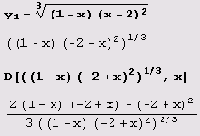
Видим, что производную можно упростить, поэтому применяем функцию FullSimplify. (Вообще говоря, это лучше делать всякий раз, когда вычисляются производные.)
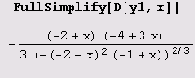
Видим, что в точках х = 1 и х = 2 производная не существует, а в нуль обращается только в точке х = 4/3. Поэтому только эти точки и являются критическими для данной функции. Однако при переходе через точку х — \ производная не меняет знака, поэтому она не является точкой экстремума. При переходе через точку х = 4/3 производная меняет знак минус на плюс, поэтому в этой точке функция имеет минимум. При переходе через точку х = 2 производная меняет знак плюс на минус, поэтому в этой точке функция имеет максимум. Вычисляем минимум и максимум.
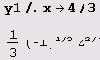
Так что локальный минимум равен

Точно так же вычисляется и локальный максимум.
y1/.x->2
0
Вот график данной функции.
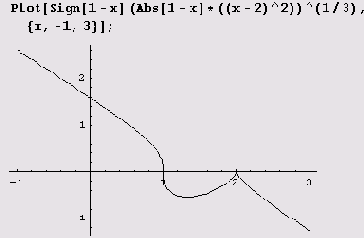
Заметьте, что для построения графика знак подкоренного выражения пришлось вынести из под корня, благодаря чему подкоренное выражение оказалось неотрицательным.
Нахождение наибольшего и наименьшего значений (глобальных экстремумов)
Если область определения дифференцируемой функции состоит из нескольких отрезков, то, чтобы найти ее глобальные экстремумы, можно сначала найти ее локальные экстремумы, а затем значения на концах отрезков. Из этих значений и нужно выбрать наибольшее и наименьшее. В общем, нет ничего сложного, если, конечно, все вышеперечисленные операции выполняются без проблем.
Нахождение интервалов выпуклости и точек перегиба
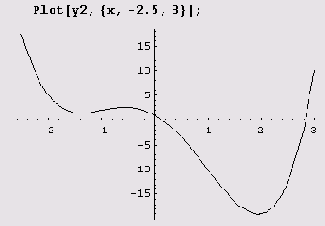
Найдем интервалы выпуклости и точек перегиба функции y2= х4-6х2—6х+1. Сначала введем функцию в систему Mathematica.
y2=x^4-6x^2-6x+1
1-6х-6х2 + х4
Теперь находим вторую производную.
D[y2,{x,2}]
-12 + 12 х2
Так как вторая производная положительна при |x| >1, то (-∞, -1) и (1, ∞) — интервалы выпуклости вниз, а (-1, 1) — интервал выпуклости вверх. Поскольку в точках х = -1 и х = 1 функция меняет направление выпуклости, эти точки являются точками перегиба. Впрочем, в этом можно убедиться и иначе: третья производная
0[у2,{х,3}]/.х->1 24
0[у2,{х,3}]/.х->-1 -24
в этих точках отлична от 0.
Вот график функции
Интегрирование
Неопределенные интегралы, или первообразные
Чтобы найти неопределенный интеграл, можно воспользоваться командой Integrate:

Но не всегда все проходит так гладко. Например, в интеграле
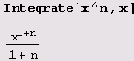
не учтен случаи n= - 1. Вот еще пример.
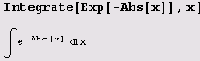
Это тавтология. Между тем данный интеграл равен еx-1 при х<0 и 1-еx в остальных случаях. (Я здесь не опустил 1 для того, чтобы интеграл был непрерывен при х = 0.) Впрочем, многие интегралы, даже технически сложные для студентов, берутся без проблем:
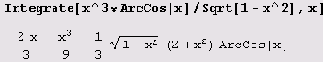
Неберущиеся интегралы остаются без изменений или выражаются через специальные функции
Integrate[Ехр[х^2], х]
1/2π Erfi [x]
Определенные интегралы
Команда Integrate вычисляет и определенные интегралы, если в ней задать не только переменную интегрирования, но и ее пределы.
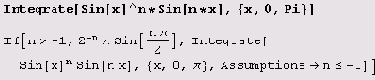
Чтобы приближенно вычислить определенный интеграл (например, неберущийся), можно воспользоваться командой NIntegrate.
Integrate[Exp[x]/x,{x,1,2}] -Gamma[0,-2]+Gamma[0,-1]
Nlntegrate[Exp[x]/x,{x,l,2}] 3.05912
Пример 10.1. Вычислим моменты инерции относительно осей координат 0х и 0у пластины с плотностью 1, ограниченной кривыми ху = 1, ху = 2, у = 2х, х = 2у и расположенной в I квадранте.
Нарисуем пластину.
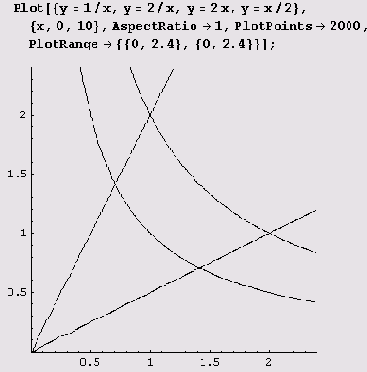
Теперь нужно вычислить
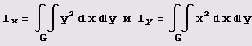
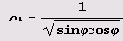 (значение р на гиперболе ху = 1) и
(значение р на гиперболе ху = 1) и
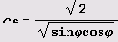
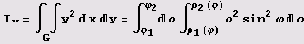 и вычислили бы этот интеграл обычным путем. Но с помощью системы Mathematica все можно сделать проще:
и вычислили бы этот интеграл обычным путем. Но с помощью системы Mathematica все можно сделать проще:
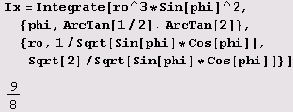
Момент инерции относительно оси 0у можно вычислить точно таким же методом. Впрочем, очевидно, что момент инерции относительно оси 0у равен моменту инерции относительно оси Ох.
Векторный анализ
Операции векторного анализа легко определить самостоятельно. Для этого полезны функции
Outer и Inner. Функция Outer позволяет создать декартово произведение двух списков. Вот как можно, например, создать список пар, первый элемент которых берется из первого списка, а второй — из второго.
Outer[List,{a,b,c}, {d, e, f} ]
{{{a,d}, {a,e},{a,fn,{{b,d},{b,e},
{b,f}},{{c,cl},{c,e},{c,f}}}
Вот пример, связанный с конкатенацией строк.

Вот числовой пример.
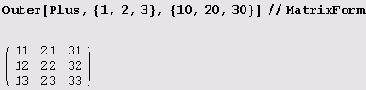
Функция Inner немного похожа на скалярное произведение. Собственно говоря, inner[f, список1, список2, g] и есть скалярное произведение, в котором умножение замещается функцией/, а сложение — функцией g.
vl = {a1, a2, a3}; v2 = {b1, b2, b3>;
Dot[vl,v2] a1 b1 + 32 b2 + a3 bз Inner[Times,vl,v2,Plus]
a1 b1 + 32 b2 + a3 bз
Теперь можем определить основные операции векторного анализа.
Вот определение градиента. gradient[f ,x_List]:=Map[D[f,#]&,x] Вычислим градиент.
gradient[f[x,у, z], {x,y,z}]
{f(0,1,0)[x, y, z], f(0,1,0)[x, y, z],
f(0,1,0)D[x, y, z]}
Теперь определим гессиан hessian[f_,x_List]:=0uter[D,gradient[f,x],x] и вычислим его:
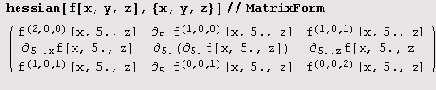
Определяем теперь лапласиан
laplacian[f_,x_List]:=Inner[D,gradient[f,x] ,x] и вычисляем его:
laplacian[f[x,y,z], {x,y,z}]
f(0,0,2)[x, y, z] + f(0,2,0)[x, y, z] f(2,0,0)[x, y, z]
Совсем несложно определить и якобиан.
jacobian[f_List,x_List]:=0uter[D,f,x] Вот пример его вычисления.
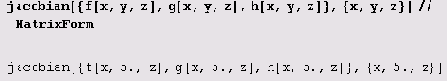
Наконец, определяем дивергенцию. divergence[f_List,x_List]:=Inner[D,f ,x] Вот пример ее вычисления.
divergence [ {f [x, у, z], g [x, у, z], h [x, y, z] }, {x, y, z} ]
h(0,1,0)[x, y, z] +
g(0,0,1)[x, y, z]+f(1,0,0)[x, y, z]
Вот еще несколько примеров выполнения операций векторного анализа.
f=x^2+x y^2+x y z^2;g=Exp[xyz];h=Sin[xyz];
gradient[f, {x,y, z}]
{2x+y2+yz2, 2xy +xz2, 2xyz}
jacobian[{f,g,h}, {x,y, z} ] //MatrixForm
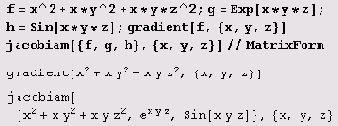
Впрочем, операции векторного анализа приходится выполнять не только в декартовой системе координат. Поэтому для выполнения этих операций имеется специальный пакет, загружаемый как обычно: <<Calculus`VectorAnalysis`. В нем предусмотрено выполнение операций в самых разнообразных системах координат — декартовой, цилиндрической, сферической, параболической, тороидальной, бисферической, сфероидальной, биполярной, параболоидной, эллиптической, эллипсоидной и т.д.
По умолчанию устанавливается декартова система координат. Вот как определить установленную систему координат и название ее переменных.
{CoordinateSystem,Coordinates[]}
{Cartesian,{Xx,Yy,Zz}}
Вот как вычислить градиент.
Grad[Xx+Sin[YyZz]] {l,Zz Cos[YyZz],Yy Cos[YyZz]}
Систему координат и название переменных можно изменить.
SetCoordinates[Cartesian[х,у,z]] Cartesian[x,у,z]
Мы установили декартову систему координат, но изменили название переменных. Посчитаем дивергенцию.
Div[{x y,x у z,Sin[x у z]}]
у+х z+x у Cos[х у z]
Установим теперь сферическую систему координат.
SetCoordinates[Spherical[r,th,ph]] Spherical[r,th,ph]
Узнаем промежутки изменения координат.
CoordinateRanges[] (0<r<∞, 0<th<π, -π<ph<π}
Напишем формулы преобразования координат.
CoordinatesToCartesian[[r,th,ph)]
{r Cos[ph] Sin[th],r Sin[ph]
Sin[th],r Cos[th]}
Найдем якобиан.
jdet=JacobianDeterminant[]
r2 Sin [th]
Шутки ради вычислим площадь поверхности сферы радиуса R
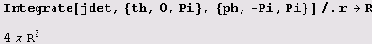
и объем сферы радиуса R:
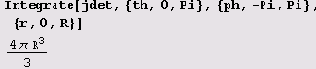
При решении многих задач весьма полезно изображать векторные поля графически. Для изображения двухмерных полей следует подгрузить пакет <<Graphics` PlotField`. Вот как с его помощью можно изобразить двухмерное поле.
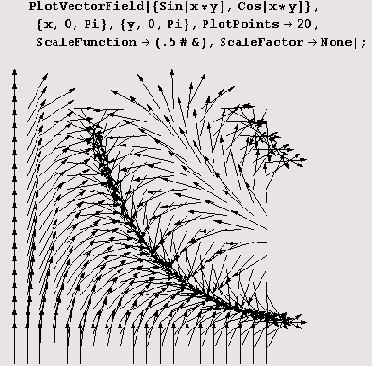
Не сложнее нарисовать и градиент скалярного поля.

Есть и функции для вычерчивания полей, заданных таблично.
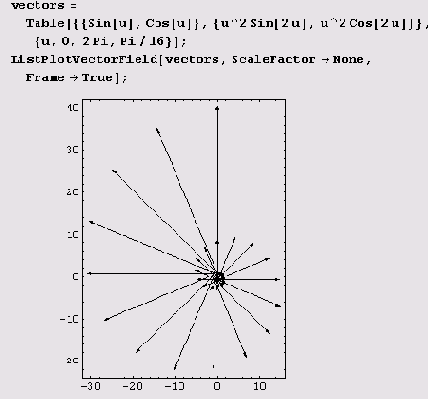
Для трехмерных полей нужно загружать пакет <<Graphics `PlotField3D`
Вот как можно нарисовать векторное поле, компоненты которого равны y/z, -x/z и 0.

Есть, конечно, и функция для изображения градиента скалярной функции. Ниже изображен градиент функции xyz.

Эти средства изображения векторных полей могут применяться, конечно, не только в векторном анализе, но и для решения других задач, например для исследования дифференциальных уравнений.
Поля направлений для дифференциальных уравнений и изоклины
Чтобы представить поведение интегральных кривых дифференциального уравнения, полезно начертить поле направлений для данного дифференциального уравнения и изоклины — кривые, пересекающие интегральные кривые под заданным углом.
Построение поля направлений для дифференциального уравнения
Давайте применим теперь средства изображения векторных полей для рисования полей направлений для дифференциальных уравнений. Если дифференциальное уравнение первого порядка разрешено относительно производной, т.е. имеет вид y' = f(x, у), то поле направлении для него строится очень просто, нужно лишь в каждой точке (х, у) задать единичный вектор, коллинеарный вектору (1,
f(x, у)). Иными словами, достаточно нормировать вектор (1,f(x, у)).
Пример 10.2. Нарисуем поле направлений для дифференциального уравнения

Совсем несложно начертить и изоклины интегральных кривых дифференциального уравнения первого порядка, разрешенного относительно производной, т.е. имеющего вид. у'= Аf(x, у).
Построение изоклин интегральных кривых дифференциального уравнения
Если дифференциальное уравнение первого порядка разрешено относительно производной, т.е. задано в виде у'=
f(x, у), то изоклины являются линиями уровня f(x, у) = С. Следовательно, задача построения изоклин сводится к построению линий уровня.
Пример 10.3. Построим изоклины уравнения у'= (у-1)х.
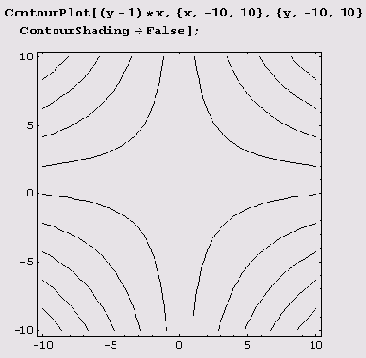
Чертежи полей направлений и изоклин, несомненно, дают весьма хорошее представление об интегральных кривых. Однако куда важнее то, что система Mathematica может интегрировать дифференциальные уравнения!
Нахождение решений дифференциальных уравнений
Решает дифференциальные уравнения функция DSolve.
Пример 10.4. Решим уравнение у'''+4у' = sec 2t.
Решение. Конечно, это линейное дифференциальное уравнение третьего порядка. Поэтому его решение содержит три произвольные постоянные и является суммой какого-нибудь решения неоднородного уравнения и общего решения соответствующего однородного уравнения. Однако система Mathematica знает все это и без нас и выдает решение сразу.
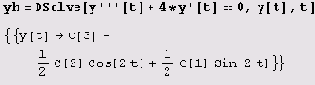
Как видите, система Mathematica обозначает произвольные постоянные через
С[1],С[2],С[3] и т.д.
Пример 10.5. Решим уравнение 4у'2-9х = 0. Решение.
yh=DSolve[4y'[х]^2-9х == 0,у[х], х]
{{у[х] ->-х3/2+С[1]},{у[х]->х3/2+С[1]}}
Заметьте, что в учебниках и задачниках это решение обычно записывается в неявной форме: (у-C)2 = х3
Пример 10.6. Решим уравнение х = y'+sin у'. Решение.
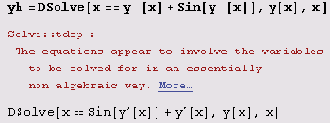
Как видим, в данном случае функция DSolve с поиском решения не справилась. Тем не менее решение может быть представлено в параметрической форме: х = p+sin р, у = p2/2+psin p+cos р+С.
Впрочем, не спешите обвинять функцию DSolve — ведь решение записано нами не в виде явной функции!
Вот еще один пример, когда решение находится как неявная функция.

Однако не следует думать, что функция DSolve сдается, если не может найти решение в элементарных функциях. Это далеко не так. Она старается применить специальные функции, о чем свидетельствует приведенный ниже пример.
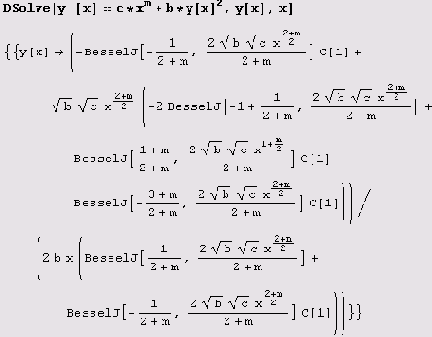
Как видите, в данном случае существенно использованы функции Бесселя.
Но все же есть случай, когда функция DSolve сдается сразу. Это происходит, если в качестве аргумента искомой функции используется выражение, не совпадающее с независимой переменной. (Такие уравнения называются функционально-дифференциальными. К счастью студентов, такие дифференциальные уравнения часто представляют собой крепкий орешек и для профессоров, поэтому в задачниках (а не в жизни!) таких уравнений встречается не очень много.)

Как видим, функция DSolve не может решить всех дифференциальных уравнений. Тем приятнее узнать, что она умеет решать некоторые уравнения в частных производных.
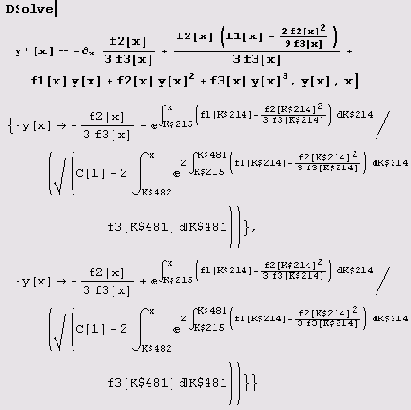
Заметьте, что фиктивные переменные, по которым производится интегрирование, обозначены в решении через K$номер.
Ниже приведен пример решения задачи Коши с помощью все той же функции
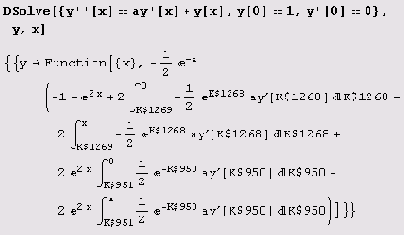
Часто решение дифференциального уравнения имеет довольно громоздкий вид, и по нему представить поведение интегральных кривых довольно сложно. В этих случаях полезно построить график решения, т.е. вычертить интегральную кривую.
Пример 10.7. Построение графика решения дифференциального уравнения. Решим дифференциальное уравнение
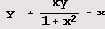
Сначала с помощью функции DSolve находим решение.
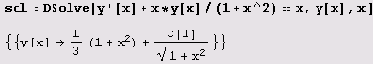
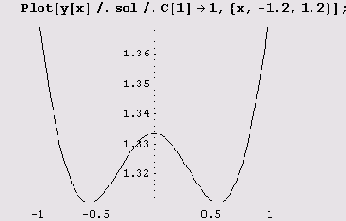
Найдя решение, можем построить его график. Для этого придется, конечно, задать значения произвольных постоянных. В данном случае это уравнение первого порядка, и потому у него только одна произвольная постоянная: с [ 1 ]. Ее значение удобнее всего задать подстановкой.
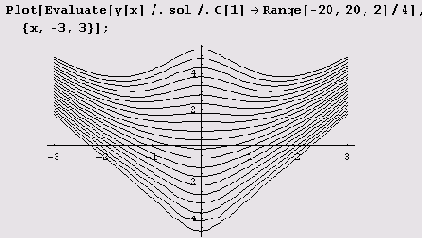
Иногда приходится строить графики решений, получающихся при различных значениях произвольных постоянных. Тогда нужно в подстановке указать список значений. Пусть, например, нужно построить графики решений для следующих значений произвольной постоянной с [ 1 ].
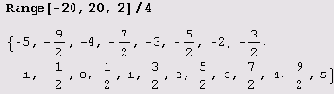
Тогда это можно сделать так.
Пример 10.8. Построение графика решения задачи Коши. Найдем решение задачи Коши для дифференциального уравнения у"= ау'+у с параметром и построим график его решения для нескольких значений параметра.
Сначала с помощью функции DSolve находим решение задачи Коши.
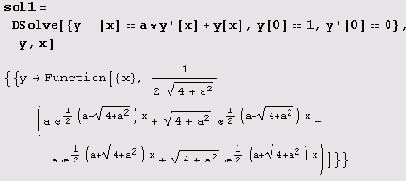
Теперь можем построить графики.
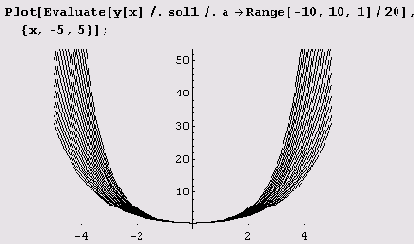
Все построенные решения проходят через точку (0, 1) и в этой точке имеют общую касательную, параллельную оси абсцисс.
Системы дифференциальных уравнений
Функция DSolve позволяет также решать системы дифференциальных уравнений.
Пример 10.9. Найдем решение системы дифференциальных уравнений х' = у, у' =
-а2х, удовлетворяющее начальным условиям х = 1, у' = 0 при t = 0.

Теперь построим графики функций x(t) и y(t) для случая, когда параметр а принимает значение 1/2.
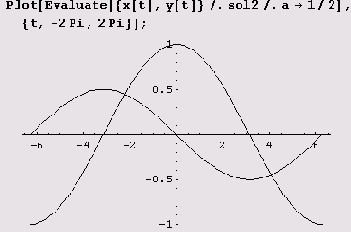
Чтобы построить фазовый портрет, нужно воспользоваться функцией
ParametricPlot.

Однако не всегда функция DSolve справляется с системами дифференциальных уравнений.
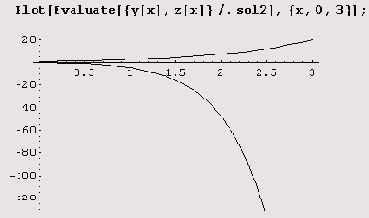
Пример 10.10. Найдем решение системы дифференциальных уравнений у"= y2+z, z'=
-2yy'+y, удовлетворяющее начальным условиям у = 0, у'= 0, z = 0 при х = 0.
sol2=DSolve[{y''[x]==y[x]^2+z[x] ,
z'[x]==-2*y[x]*y'[x]+y[x], у[0]==1,у'[0]==l,z[0]==0},{y,z},{x})
DSolve [{у"[x]==y[x]2+z[x],
z'[x]=y[x]-2y[x]y'[x],y[0]==1,y'[0] = 1,z[0] == 0},{y, z),{x}]
Как видите, несмотря на то что в данном случае решением является пара функций у = ё*, z - ef—e1*, функция DSolve не смогла найти его. В таких случаях, как и одно дифференциальное уравнение, так и систему дифференциальных уравнений приходится решать численно. Для этого можно воспользоваться функцией NDSolve. Вызов ее отличается от вызова функции DSolve лишь тем, что в нем нужно указать интервал, на котором ищется решение.
sol2=NDSolve[{y''[x]==y[x]^2+z[x],
2'[х]==-2*у[х]*у'[х]+у[х],
у[0]==1,у'[0]= =1, z[0]==0}, {y,z},{x,0,10}]
{{y->InterpolatingFunction[{{0.,10.}},<>],
z->InterpolatingFunction[{{0.,10.}),<>]}}
В данном случае уравнения представлены в виде интерполяционных функций для у(х) и z(x) на интервале (0, 10). Хотя это и не аналитические выражения, они позволяют вычислить значения наших функций — решений системы дифференциальных уравнений — в любой точке интервала (0, 10).
{y[5],z[5]}/.sol2
{ {148.413,-21878.}}
Несложно представить решение и в табличном виде. Ниже, например, приведена таблица значений функций у(х) и z(x) на отрезке [1, 5].

Конечно, это совершенно нечитаемо, и лучше превратить это в обычную таблицу.
| x |
y(x) |
z(х) |
| 1 |
2.71828 |
-4.67077 |
| 1.2 |
3.32012 |
-7.70305 |
| 1.4 |
4.0552 |
-12.3894 |
| 1.6 |
4.95303 |
-19.5795 |
| 1.8 |
6.04965 |
-30.5486 |
| 2. |
7.38906 |
-47.2091 |
| 2.2 |
9.02501 |
-72.4259 |
| 2.4 |
11.0232 |
-110.487 |
| 2.6 |
13.4637 |
-167.808 |
| 2.8 |
16.4446 |
-253.982 |
| 3. |
20.0855 |
-383.343 |
| 3.2 |
24.5325 |
-577.312 |
| 3.4 |
29.9641 |
-867.883 |
| 3.6 |
36.5982 |
-1302.83 |
| 3.8 |
44.7012 |
-1953.49 |
| 4. |
54.5981 |
-2926.36 |
| 4.2 |
66.6863 |
-4380.38 |
| 4.4 |
81.4508 |
-6552.79 |
| 4.6 |
99.4843 |
-9797.64 |
| 4.8 |
121.51 |
-14643.3 |
| 5. |
148.413 |
-21878. |
Эта таблица, несомненно, более читабельна, чем список, но гораздо нагляднее выглядят графики функций. Никаких проблем с их построением не возникает.
В системе Mathematica предусмотрены всеВ системе Mathematica предусмотрены все функции, необходимые для выполнения основных алгебраических и аналитических операций. Очень легко, в частности, выполняются всевозможные подстановки. Их можно выполнять глобально, одновременно, повторно, по образцу. Предусмотрены действия с дробями и со степенями, раскрытие скобок, приведение подобных. Имеются различные функции для выполнения операций над многочленами, в том числе и весьма трудоемкие для ручного счета, такие как разложение на множители. Легко вычисляются наибольший общий делитель и наименьшее общее кратное полиномов, а также результант. Что касается поля рациональных дробей, то для него предусмотрены не только четыре основных действия (они предусмотрены для любых выражений), но и более специфические операции вроде сокращения, раскрытия произведений и целые положительных степеней в числителе, а также разложение рациональной дроби на простейшие, разложение числителя и знаменателя на множители, приведение к общему знаменателю с последующим сокращением общих множителей числителя и знаменателя в полученной сумме. Ряд функций предназначен для упрощения результатов вычислений. В области линейной алгебры также предусмотрен широкий набор операций: вычисление различных произведений (векторов и матриц), норм (векторов и матриц), матричные операции (в том числе обращение матриц и нахождение псевдобратных матриц). Есть средства решения систем линейных уравнений, в том числе и несовместных (нахождение псевдорешений). Что касается операций анализа, то и они, если не считать перехода к пределу, реализованы превосходно. Лишь при вычислении пределов нужно соблюдать осторожность: в случае несовпадения односторонних пределов любой из них система Mathematica может подсунуть в качестве двустороннего. Система Mathematica весьма успешно справляется с вычислением производных (в том числе и смешанных) и интегралов (определенных и неопределенных). После вычисления производных полученный результат иногда нуждается в упрощении. Зато разложение функций в ряд Тейлора, да и действия над рядами выполняются безукоризненно. Все это позволяет произвести довольно полное исследование функций (определить их интервалы монотонности, найти локальные и глобальные экстремумы, найти интервалы выпуклости и точки перегиба) и построить их графики. При необходимости исследовать скалярные или векторные поля, задаваемые функциями нескольких переменных, можно воспользоваться функциями Outer и Inner для определения операций векторного анализа. Легко определяются градиент, гессиан, лапласиан, якобиан и дивергенция. Впрочем, все нужные определения (причем в самых разнообразных системах координат) имеются в пакете Calculus`VectorAnalysis`. Функциями этого пакета можно воспользоваться и для решения других задач, например для исследования дифференциальных уравнений. Для нахождения решений дифференциальных уравнений и их систем используется функция DSolve. Она может не только находить общие решения, но и учитывает дополнительные условия (начальные, граничные) и потому может решать, например, задачу Коши. Если же функция DSolve не может найти решение в аналитическом виде, для численного решения можно воспользоваться функцией NDSolve |