Новый вид науки

Боюсь, я несколько превысил отведенный мне лимит времени, хотя и не успел полностью познакомить вас ни со всей Математикой, ни со всеми функциями системы Mathematica. Памятуя опыт Никола Бурбаки, я и не ставил перед собой такой задачи. Просто я хотел показать, что с помощью пятистрочечных программ, написанных на языке системы Mathematica, школьники, студенты, аспиранты, инженеры и научные сотрудники самых разных профилей могут успешно решать свои задачи. И если вы готовы идти дальше и применять систему Mathematica в своей работе, — я достиг цели, поставленной перед написанием этой книги. Жаль, конечно, что нет такой одной универсальной книги, в которой была бы изложена вся-вся Математика. Даже в этой тоненькой книжечке были затронуты вопросы, о которых пятитомная Математическая энциклопедия даже не упоминает. И уж тем более это справедливо для пятитомного (в семи книгах!) курса высшей математики, написанного В. И. Смирновым. Хотя многотомное собрание сочинений Бурбаки является, вероятно, одним из наиболее полных, и оно не может рассматриваться как абсолютно полное. Впрочем, в качестве одной из наиболее полных, если не самой полной, энциклопедий математики можно рассматривать, на мой взгляд, и систему Mathematica. (Конечно, она и неполна, и многотомна. Ведь ядро, хотя и расширяется от версии к версии, охватывает далеко не все разделы математики. Дополнительные сведения содержатся в пакетах.) Но это не простая, а активная энциклопедия: она не просто выдает информацию, а выполняет необходимые действия (вычисления, например). Как и при использовании любой другой, при применении этой энциклопедии требуется определенная подготовка, — из этой книги вы почерпнули необходимые начальные сведения. В отношении удобства пользования система Mathematica уникальна: ею систематически пользуется сам автор — Стив Вольфрам! Более того, именно с ее помощью Стив Вольфрам открыл новый вид науки! Как это случилось? Как и все сложное, очень просто. Стив начал искать ответ на вопрос: почему простые объекты могут образовывать сложную конструкцию и насколько сложным может быть поведение простых систем?

Теория универсальности, или насколько сложным может быть поведение простой динамической системы

Возможно, заголовок кажется вам заумным. Может быть, это просто оттого, что вы никогда не слышали о динамических системах. Не беспокойтесь, все очень просто: в данном случае под динамической системой понимается любая система, в которой некоторый параметр определяется рекуррентным уравнением х_n+1 =f(x_n, r). В частности, под динамической системой можно понимать числовую последовательность, определяемую таким уравнением. Где встречаются такие последовательности? Да почти повсюду. Вот простейший пример.

Допустим, нас интересует изменение численности какого-либо вида животных в определенном районе. Один раз в год мы считаем их и получаем число х. По этим данным можно построить последовательность x1, х2 ..., хn, ... (n = 1 соответствует первому измерению). Логично предположить, что среди этих чисел есть какая-то закономерность. Естественно ожидать, что численность популяции в (n+1)-й год х_n+1 зависит от того, сколько животных было год назад, т. е. от величины х_n. Поэтому в простейшем случае х_n+1 = f(x_n, r).

Здесь f— непрерывная функция; r— некий параметр, который зависит от биологических особенностей рассматриваемого вида. В популяционной генетике часто предполагается, что х_n+1 = rx_n(N-x_n).

Эта формула показывает, что численность вида быстро растет, пока она мала (x_n<N), и начинает убывать, когда животных становится слишком много. Если сдeлать замену переменных х_n = x'_nN, r = r'/N, то в новых переменных наше уравнение будет иметь вид х'_n+1 = г' х'_n(1—х'_n). Тем самым мы элиминировали параметр N и привели уравнение к более естественной для математиков форме. Теперь по самому смыслу задачи 0<х'_n<1. Простоты ради опустим штрихи и займемся исследованием этой более простой динамической последовательности.

Что же будет происходить с различными видами (т.е. с последовательностями х_n+1 = rх_n(1— х_n) с различными r) по прошествии достаточно долгого времени? Чтобы ответить на этот вопрос для нашей простейшей модели, достаточно выяснить, как будет вести себя последовательность {х_n} при различных значениях г. Давайте проведем численный эксперимент. Сначала дадим нужные нам определения.

х[r_][0]=0.5;

 x[r_][n_]:=x[r1[n]=r х[r][n-1]<1-х[r][n-1])

Таким образом, мы задали начальный член последовательности х₀ = 0,5. Теперь положим, r = 3,83, и вычислим первые пятьдесят членов последовательности.

Вот как все это выглядит на графике.

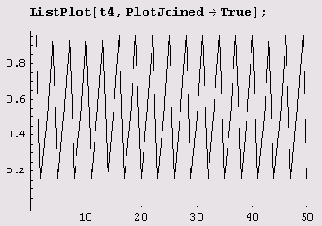
Вот теперь действительно есть чему удивиться! Численность популяции оказалась периодической функцией.

Конечно, здесь проведены вычисления только дляr = 3,83, а нам нужно провести вычисления для разных r. Давайте проведем их для 250 значений г, равномерно распределенных между r = 2,8 и r = 4,0.

t1=Table[{r,x[r][n]},{r,2.8,4,1.2/249},{n,101,300}];

Здесь для каждого из 250 значений г строится список х_n для n- 101, ..., 300. Вот что получается (конец опущен).

Чтобы построить график, этот список нужно сделать плоским:

toshow=Flatten[t1,1);

Теперь список будет иметь вид (конец опущен)

{{2.8,0.642857},{2.8,0.642857},{2.8,0.642857},{2.8,0.642857},

{2.8,0.64 2857},{2.8,0.642857},{2.8,0.642857},{2.8,0.642857},

и мы можем построить график, наглядно демонстрирующий поведение последовательности {*„} при различных значениях параметра г в отображении х_n+1= rх_n(1-х_n).

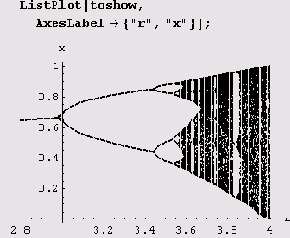
Из графика видно, насколько сложно зависит поведение популяции от r.

Еще раз обратим внимание на простенькую формулу х_n+1 = rх_n(1-х_n). При небольших г (0<r<1) х_n стремится к нулю независимо от выбора XQ. Судя по формуле хn+1= rx_n(1-х_n), вид, численность которого вначале равна XQ, выжить не может, сколько бы животных ни было вначале. Поведение последовательности в этом и в других случаях удобно представлять графически. Нарисуем кривую y=f(x) при заданном значении г и прямую у = х. Отложим х по оси абсцисс, проведем вертикаль до пересечения с кривой у —/(х) (точка А), а затем из точки пересечения горизонталь до пересечения с линией у = х (точка В). Теперь вновь проведем вертикаль до пересечения с кривой у = f(x), что даст нам точку С с координатой х₂. Тогда х₂ =f(х₁). Взяв точку х₂ за начальную и повторив все те же операции, получим х₃, затем х₄ и т.д.

Теперь рисуем график, чтобы представить поведение последовательности х_nпри n->∞.

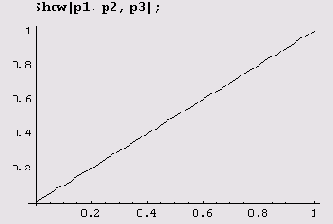
Из рисунка видно, что х_n->0 при n->∞.

Из формулы х_n+1 = rхn(1-хn) следует, что функция f(x) переводит отрезок [0, 1] в отрезок [0, r/4]. Если r<4, то все значения х„ лежат на отрезке [0, 1] при условии, что 0<х<1. Так что формула х_n+1 = rхn(1—хn) задает отображение отрезка [=, 1] в себя.

Пусть теперь r немного больше 1, например r = 2.

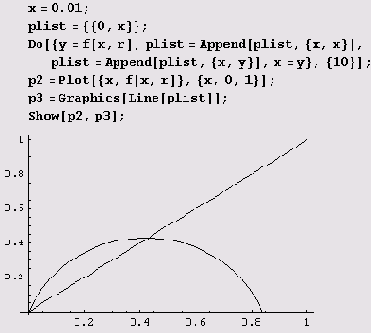
Видим, что при этом значении г последовательность {хn} ведет себя по-другому: хn стремится к постоянному, отличному от нуля, значению хn при n—>∞. В применении к исходной биологической задаче это означает, что численность такого вида по прошествии нескольких лет стабилизируется и перестанет меняться со временем.

Значение х* может быть найдено из уравнения х* = f(x*).

Все точки, удовлетворяющие этому уравнению, являются неподвижными точками функции f, так как если х, = х', то и х2 = х', хn = х' при любом n.

При r<1 квадратное уравнение х=rх(1- х) имеет один неотрицательный корень х=*0. При t->1 неотрицательных корня два: х* = 0 nх* = (t-1)/r. При r= 1 происходит бифуркация: неподвижная точка х' = 0 теряет устойчивость, а вновь появившаяся точка становится устойчивой.

Можно довольно просто определить, будет ли устойчивой неподвижная точка х отображения f[x]. Пусть х„ = х + Δхn, где Δхn — малое число. Если точка устойчива, то с ростом n величина |Δхn| должна уменьшаться. Перепишем формулу х_n+1 = f(xn, r) в виде

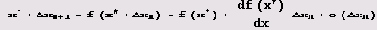
Если в последнем равенстве опустить член о(Δхn), то полученное приближенное равенство будет выполняться тем точнее, чем меньше Δхn (мы пренебрегли членами, пропорциональными (Δхn)², (Δхn)³ и т.д.). Поскольку x* = f(x), то

И для того чтобы Δх_n+1->0 при n->∞, должно выполняться неравенство

Это и есть условие устойчивости точки х*.

Будем дальше увеличивать параметр r. Поведение системы снова изменится: в последовательности {хn}, начиная с достаточно больших и, будут чередоваться числа, близкие к некоторым двум числам я, и а2. (Точнее говоря, последовательность устроена так, что x_2n+1->a₁, х_2n+1->n₂ при n->∞) Эти числа связаны соотношениями а1 = f(а₂), а₂ = f(а₁). Иными словами, в этом случае отображение х_n+1 = rхn(1—хn) имеет устойчивый цикл с периодом 2. Обозначим этот цикл 52. Наличие цикла S* в нашей модели означает, что численность популяции будет меняться с периодом в 2 года.

Выясним, как выглядят циклы на графике. Для этого определим программу cobwebPlot.

Сначала протестируем эту программу.

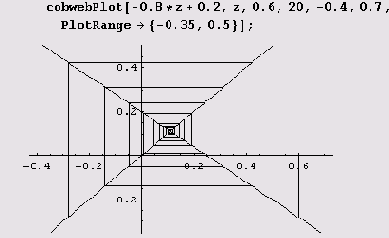
Теперь нарисуем картинку для случая г = 1.

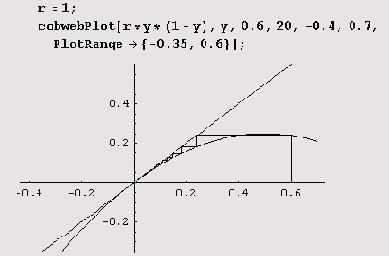
Теперь нарисуем картинку для случая г = 2.

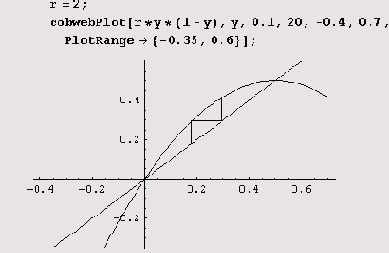
Наконец, выясним, как выглядит двойной цикл (цикл с периодом 2).

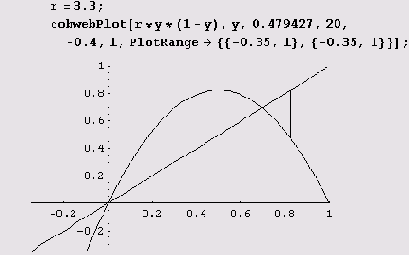
Переход от неподвижной точки, которую можно считать циклом S1, к циклу 52 произошел в результате бифуркации, которая получила название бифуркации удвоения периода. Точка х при этом не исчезла и осталась неподвижной, однако величина

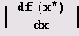
При дальнейшем увеличении г поведение последовательности {хn} опять изменяется. Возникает цикл S⁴: х_4n->а₁, x_4n+1->a₂, х_4n+1->a₃> x_4n+3->а₄ ПРИ n->∞, причем а2 = f(a1), а3=f(a2), аn =f(an). Численность популяции начинает колебаться с периодом в 4 года.

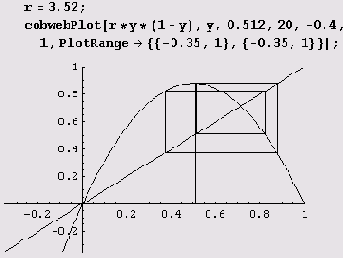
Но и это еще не все. Приведем еще несколько примеров поведения наших последовательностей.

Последовательно увеличивая значение параметра, мы увидим циклы S⁸, S¹⁶, S³² и т.д. При этом каждый раз цикл S² теряет устойчивость, и устойчивым становится цикл S² . Наконец, при некотором значении г (его иногда обозначают г„) формула x_n+1 = rхn(1-хn) дает уже непериодическую последовательность {xn}.

Полученная нами картина оказалась очень интересной. Во-первых, в поразительно простой модели х_n+1 = rхn(1-хn) заложено очень сложное поведение. Во-вторых, в ней удается проследить большое количество бифуркаций, приводящих к усложнению решения. Сделать это в более сложных моделях гораздо труднее. Как это ни удивительно, но пока встречались только циклы, период которых равен степени 2.

Чтобы понять, чем это вызвано, и изучить поведение модели более подробно, наряду с функцией f(x) удобно рассмотреть отображение f(f(х)), обозначаемое далее через f²(х), и вообще положить f^n+l(x) =f(fⁿ(x)), считая, конечно, что f(n) =f(х).

Построим график f(x).

Вот нужные нам определения.

f[х_,r_]:=г*х*(1-х);

ff[x_,r_,n_]:=Module[{t=x},Do[{t=f[x,r],x=t},{n}];t]

Сначала рассмотрим случай устойчивой неподвижной точки. Вот что получим для случая г = 3.

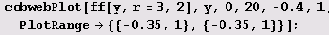
Теперь рассмотрим случай устойчивого цикла S².

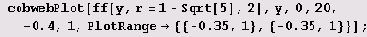
График функции f(x) пересекается с прямой у = х во всех неподвижных точках отображения / (ведь для любой неподвижной точки х отображения f имеем f²(х*) = f(f(x')) = f(x') = (х'), а также в точках, принадлежащих циклам 52 (потому что а2 = f(a1) = f(f(a2)) и а1 = f(a2) = f(f(f()))- Увеличивая параметр r, мы растягиваем функцию f(x) вдоль оси у. И если при некотором значении г линии у = х и у = fix) пересекаются в одной точке, то с увеличением г могут появиться еще две точки пересечения. Они-то и будут определять цикл S2.

Таким образом, переход от 51 к 52 в отображении f(x) обусловлен тем, что в отображении f (х) одна из неподвижных точек теряет устойчивость и в ее окрестности появляются две новые устойчивые неподвижные точки. Здесь вновь происходит бифуркация. Рассматривая функции f⁴(х), fⁿ(x) и так далее, можно посмотреть, как происходят следующие удвоения.

На примере модели х_n+1 = rхn(1- хn) можно понять не только качественные, но и удивительные количественные закономерности. Чтобы проследить за ними, построим график х(r): по оси х будем откладывать х₁, х₂, ..., лежащие на устойчивом цикле, по оси г — значения параметра. Циклу S* будут соответствовать две точки на одной вертикали, циклу S1 — четыре и т.д. Тогда получим ранее приведенный график, отражающий усложнение устойчивых циклов в отображении х_n+1 = rхn(1-хn), происходящее в результате бифуркаций удвоения периода.

Обозначим через R1, R2, R}, ... те значения параметра г, в которых происходили удвоения, а через r1, r2, г3, ... — значения параметра, при которых х= 1/2 является элементом цикла S2, S4, Ss и т. д. Введем также величины d1, d2, ..., dn, .., равные расстоянию между х = 1/2 и ближайшим к нему элементом цикла S² при r = r_n. Расчеты показали, что числа f(x) и r_n при больших и ведут себя как геометрическая прогрессия со знаменателем a = 4,6692016... Другими словами,

d_n/d_n+1 также имеет предел, равный некоторому числу а, причем а = 2,5029078...

Что будет, если вместо функции х_n+1 = rхn(1—х_n) взять любую другую симметричную функцию, которая имеет на отрезке [О, 1] один максимум и около вершины близка к квадратичной параболе. Пусть в ней также происходит бесконечная последовательность бифуркаций удвоения при изменении некоторого параметра. Оказалось, что в любой такой модели числа а и 5S будут одними и теми же! Более того, независимо от вида функции предел lim(-a)ⁿf²ⁿ[(x-0,5)/(-a)ⁿ,r_n] существует и будет одной и той же универсальной функцией, обозначаемой часто через g₀(х).

Эти удивительные закономерности были обнаружены и поняты американским математиком М. Фейгенбаумом в 1978 году. В силу универсальности чисел а и 5 и функции g₀(x), a также других функций такого типа эту теорию называют теорией универсальности.

Что же означают эти результаты?

В природе можно выделить два совершенно различных на первый взгляд типа явлений. Одни — регулярные и упорядоченные. Это большинство процессов, используемых в технике и технологии, процессы, в которых возникают структуры. Как правило, ход таких процессов можно предсказывать, зная управляющие ими законы.

Другие процессы — случайные, хаотические. К ним относится турбулентное движение жидкости, шумы в различных электронных системах и т.д. Они требуют другого, статистического описания, которое позволяет получить некоторые усредненные характеристики процессов. Такие явления также очень важны, но используются гораздо реже из-за их сложности и недостаточной изученности. В одних случаях турбулентное движение жидкости позволяет транспортировать уголь, руду и многое другое по трубам. В других — с турбулентными вихрями приходится бороться. Хорошо зная законы турбулентного движения, можно было бы строить более быстрые и экономичные суда и самолеты.

Теория Фейгенбаума приводит к парадоксальному выводу: между хаосом и порядком есть глубокая внутренняя связь. Непериодический, случайный процесс возникает как предел все более сложных структур (циклов S²ⁿ). Хаос возникает как сверхсложная организация (цикл S² )! Этот вывод является очень общим: он может относиться к моделям экологии, гидродинамике — к любым системам, где есть последовательность бифуркаций удвоения периода.

Возможно, вы подумали, что сложность взаимоотношений порядка и хаоса, имеющая место в данной модели, связана с участием вещественных чисел. Тогда вспомните график функции Эйлера, график количества единиц в двоичной записи целых чисел. На этих графиках, где нет ничего, кроме целых чисел, также наблюдается сложная картина чередования хаоса и циклов.

Еще более сложная .картина может наблюдаться в многомерном (например, в двухмерном) случае. Если модель к тому еще и дискретная, то можно говорить о клеточных автоматах.

Клеточные автоматы

Клеточный автомат — это совокупность клеток пространства (возможно, многомерного), каждая из которых может находиться в одном из нескольких состояний. Клеточные автоматы представляют собой дискретную модель, основанную на рекуррентных правилах: следующий шаг является результатом применения правил к конфигурации, достигнутой на предыдущем шаге. Вот как эволюционирует Вселенная (иногда ее удобно рассматривать тоже как клеточный автомат), населенная такими автоматами. Все пространство (Вселенная) разбито на клетки, каждая из которых может находиться в одном из нескольких состояний. (Сами клетки тоже можно рассматривать как простейшие автоматы. Тогда можно сказать, что в некоторых клетках "живут" простейшие автоматы.) Эти клетки (простейшие автоматы) подчиняются определенным правилам (законам населяемой ими Вселенной). Сами правила обычно настолько просты, что могут быть занумерованы числами. Однако получающиеся в результате жизнедеятельности таких организмов конфигурации могут быть очень сложными. Иными словами, сообщество примитивных организмов (т.е. организмов, живущих по весьма примитивным правилам) может создать весьма сложную социальную структуру. Возможна и другая трактовка: хотя сами элементарные частицы устроены просто и подчиняются весьма простым законам, они образуют нашу Вселенную. (Разумеется, Вселенная устроена весьма сложно.)

Чтобы увидеть все это на экране, нам понадобится предварительно познакомиться с несколькими функциями. Функция CellularAutomaton [правило, начальная конфигурация, число шагов] генерирует представление (список) конфигурации, в которую переходит начальная конфигурация после указанного числа шагов в соответствии с заданным правилом. Функция Raster [{{а₁₁, а₁₂, ... }, ... }] является двухмерным графическим примитивом, который представляет прямоугольный массив ячеек в градациях серого. (Состояние клетки удобно изображать определенным цветом или градацией серого.) Вот пример.

Конечно, рисунок, особенно при большом числе клеток, может выглядеть и более замысловато.

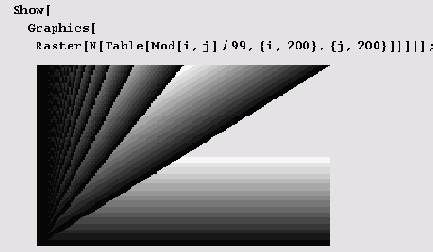
-это уже нечто вроде приглашения в театр, где актерами будут клеточные автоматы. Но вначале увертюра. Нам понадобится еще одна функция.

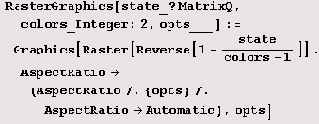
Теперь используем правило 481, и занавес поднят!

Естественно, здесь мы видим только конечный результат. Давайте теперь посмотрим, как эволюционирует Вселенная с одним единственным атомом (число 1), окруженным пустотой (нулями) по правилу 30. Вот начальное состояние:

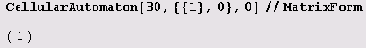
А вот та же Вселенная через три секунды (секунда = 1 шаг):

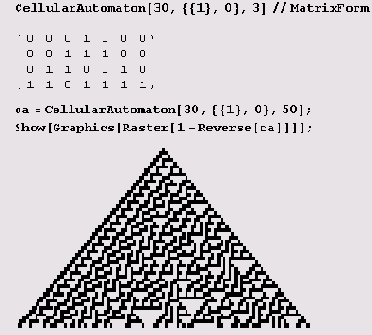
Здесь, правда, для удобства наблюдателей, приведен негатив Вселенной, притом перевернутый!

Отвечая на вопрос Наполеона о необходимости Создателя, можно сказать, что если у этой Вселенной и был Создатель, то им был Стив Вольфрам!

Несомненно, самым известным двухмерным клеточным автоматом является игра "Жизнь", придуманная Джоном Конвеем в 1970 году. Именно она прославилась своими многочисленными узорами и способностью заставлять людей тратить уйму машинного времени на поиски еще более интересных узоров! В этой игре с очень простыми правилами есть все: катапульты, ружья, паровозы, планеры, циклы, пожиратели планеров, крокодилы, стационары, семафоры и аннигиляция. Крокодил, например, является пожирателем планеров, поскольку он проглатывает планер без всякого ущерба для себя. С помощью функции CellularAutomaton вы можете разыграть захватывающие сценки из этой Вселенной!

А если клетки в придуманной вами Вселенной будут достаточно малыми, а процесс эволюции — достаточно длительный (например, 80 шагов), вы можете увидеть самоподобные конфигурации, и тогда вспомните о фракталах, множествах Мандельброта и Жулиа! Для обстоятельного разговора о них, конечно, нужна отдельная книга, и, возможно, не одна. Ну а мы, кратко обсудив в главе 1 применение системы Mathematica к изучению фракталов, теперь завершили своеобразный цикл 5" (очень редкий — с нечетным показателем!), ведь эта глава — одиннадцатая. И последняя — в этой книге. И если ваше знакомство с системой Mathematica продолжится, я считаю, вы прочли эту книгу недаром. Ну а сейчас пришло время сказать, как это знакомство продолжить. Иными словами, сейчас я собираюсь вкратце перечислить хотя бы некоторые ресурсы по системе Mathematica и по ходу дела указать на то, что осталось "за кадром".

Система Mathematica может помочь решать

Система Mathematica может помочь решать задачи школьникам, студентам, аспирантам, инженерам и научным сотрудникам самых разных профилей. Система Mathematica — это не только интеллектуальный калькулятор, используемый в интерактивном режиме, но и система программирования, сервер и помощник с энциклопедическими познаниями в области математики. Как показал ее сам автор — Стив Вольфрам, — она может даже помочь открыть новый вид науки!